利用欧拉角旋转正交_正交矩阵之旋转矩阵

内容介绍：

解释为什么一个行列式为1的正交矩阵称为旋转矩阵

一个

阶实矩阵

，如果满足

则被称为正交矩阵。正交矩阵有下面的性质

• 是正交矩阵当且仅当
  的行(列)向量组为
  的一组标准正交基。

注意：在

中，利用

施密特正交化法，可以轻松将任意一组基转化为标准正交基。

为了解答“行列式为1的正交矩阵称为旋转矩阵”的原因，我们需要先了解下面两点。

一、矩阵是如何表示线性变换的

点击如何理解线性变换,了解线性变换与矩阵的关系。

实际上，在取定

中的标准正交基

后，每一个矩阵

都确定了

上唯一一个线性变换

， 使得对任意

上图中红色与蓝色的点分别代表一个二阶矩阵的第一列与第二列。矩阵给定后，这两个点就确定下来。很容易看出上图的线性变换将原坐标系的基向量(1,0)^T,(0,1)^T的映射到了红色与蓝色向量。

二、如何理解正交矩阵的行列式为正数

考虑正交矩阵的

个列向量组成的标准正交基（单位直角坐标系），行列式为正数，代表了列(行)向量之间的相对位置关系。

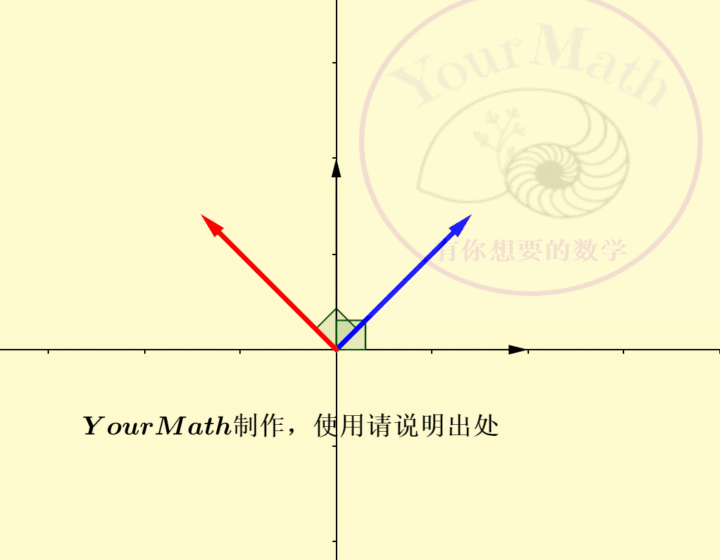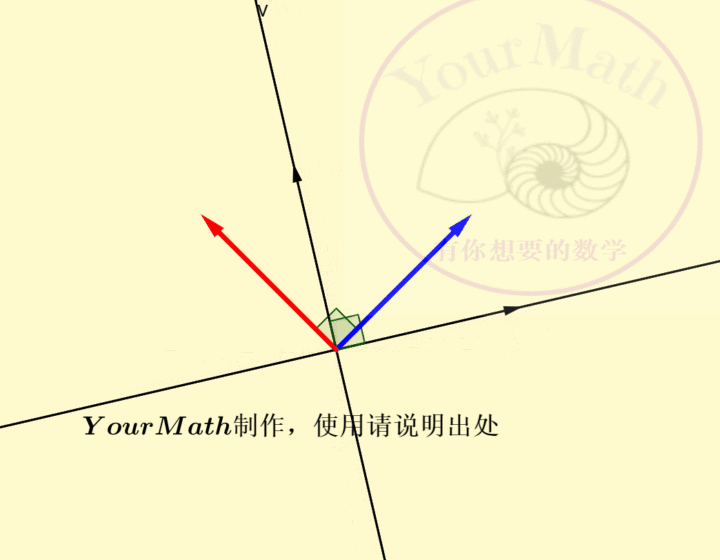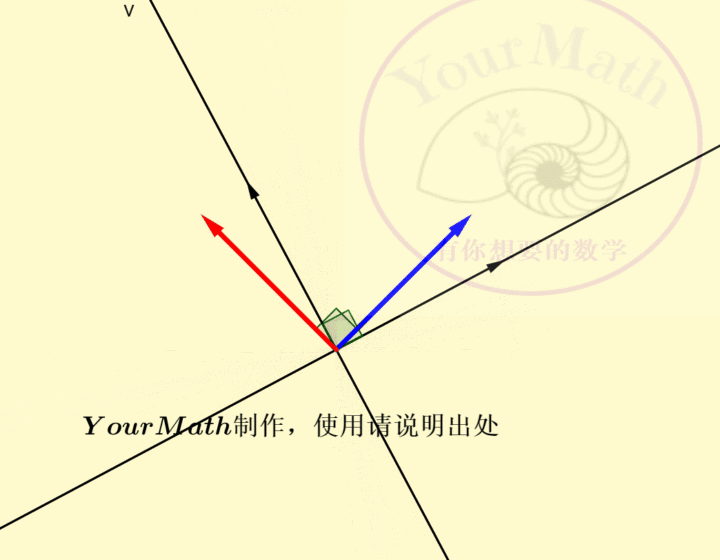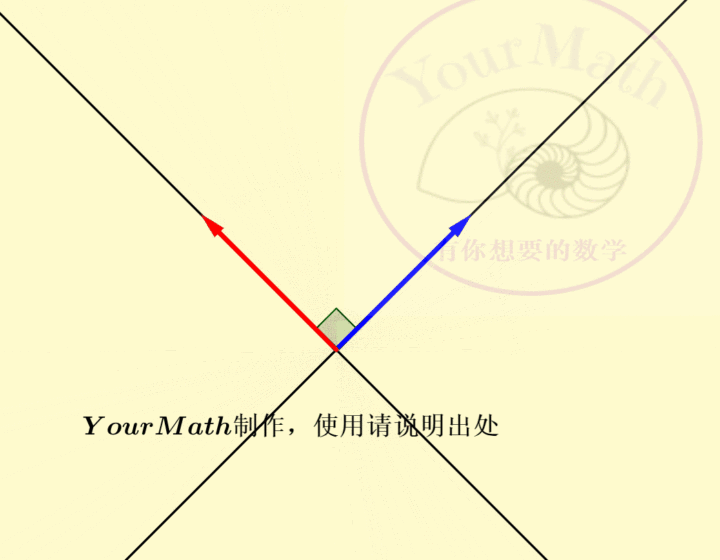
2.1. 二阶正交方阵，

在如何理解二阶行列式的符号中，我们知道了如何判断一个二阶行列式的符号。一个行列式为1的二阶正交方阵

中，

逆时针旋转90度可以得到

2.2 三阶正交方阵

设3阶正交矩阵

, 则

由外积的计算方法 可以知道：

从而

在三维空间中构成一个右手系。

三、总结。

如果把一个正交方阵

的列向量组，理解为空间中的一个单位直角坐标系。那么

意味着，

的相互位置关系，与原坐标系

-轴，

-轴，

-轴正方向的相互关系是一致的。从而，一个适当的旋转就可以让原来的坐标系变成

的列向量表示的坐标系，这恰好是这个正交矩阵所代表得线性变换。

蓝色向量、红色向量为一个二阶正交矩阵得第一、二个列向量，行列式为正意味着蓝色向量逆时针旋转90度得到红色向量。原坐标系的两个基向量经过旋转变换即得到这两个单位正交向量。

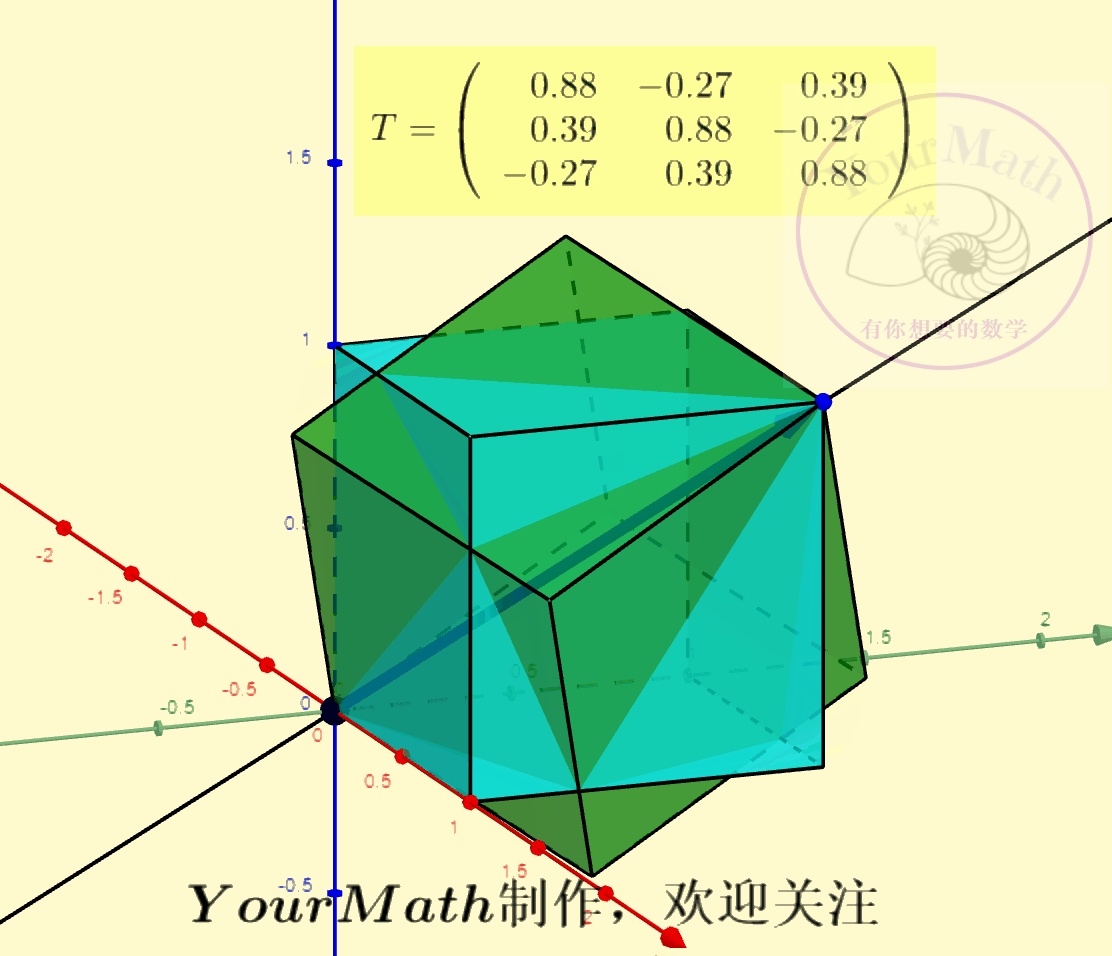
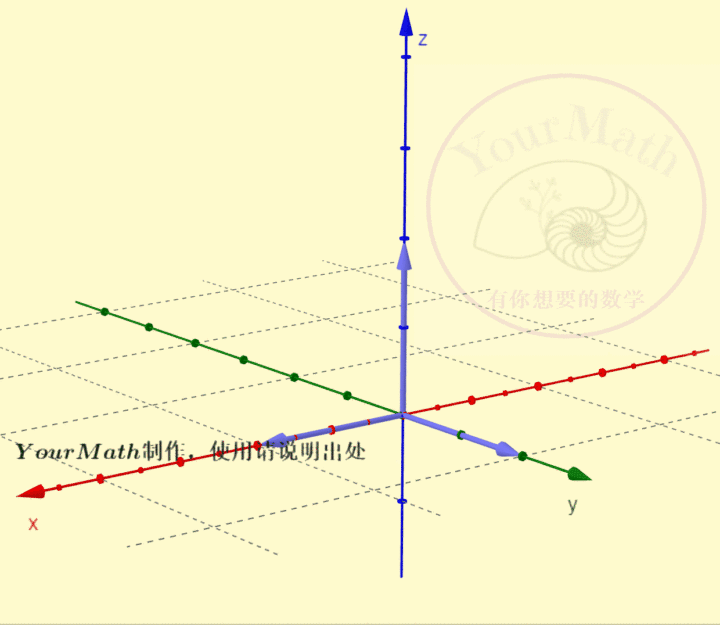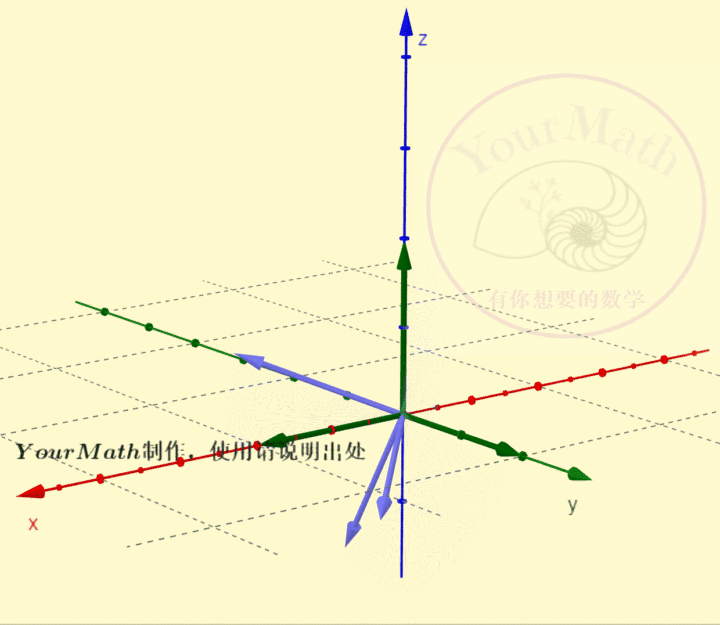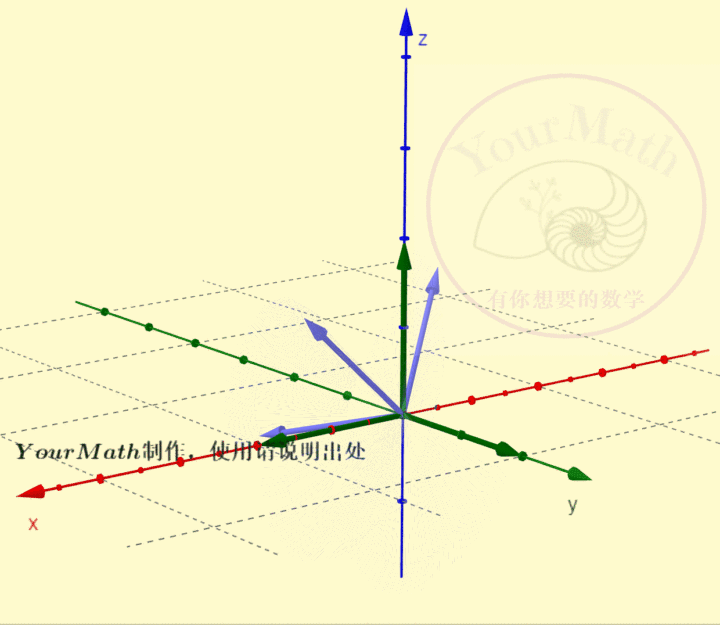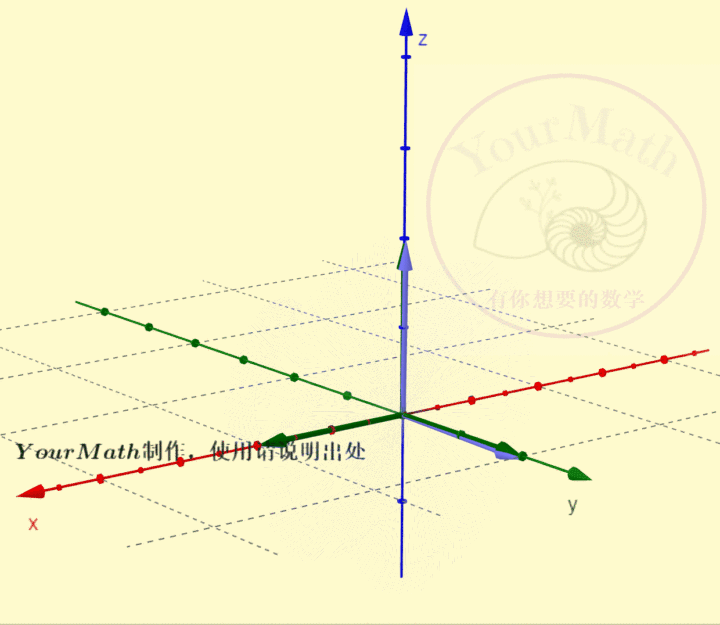
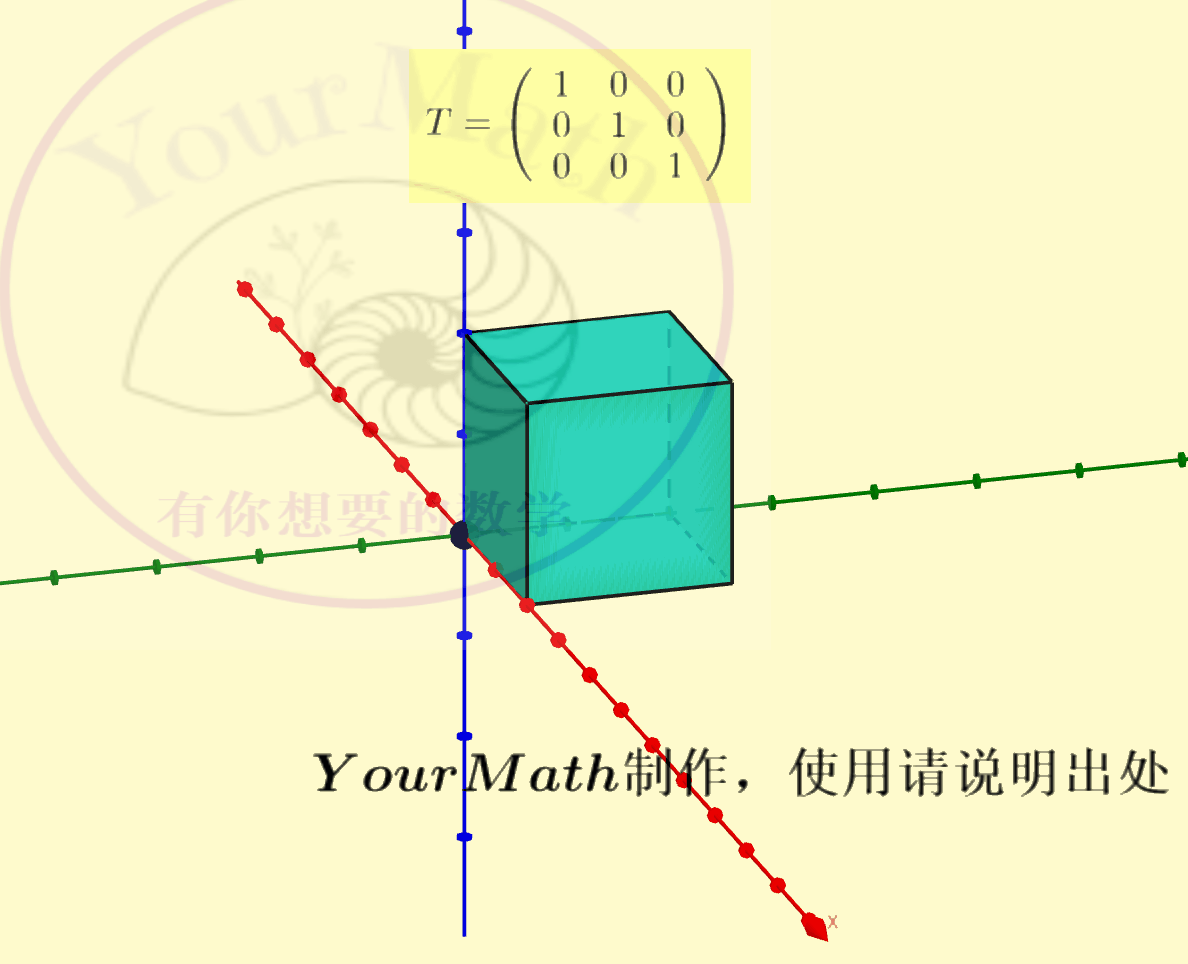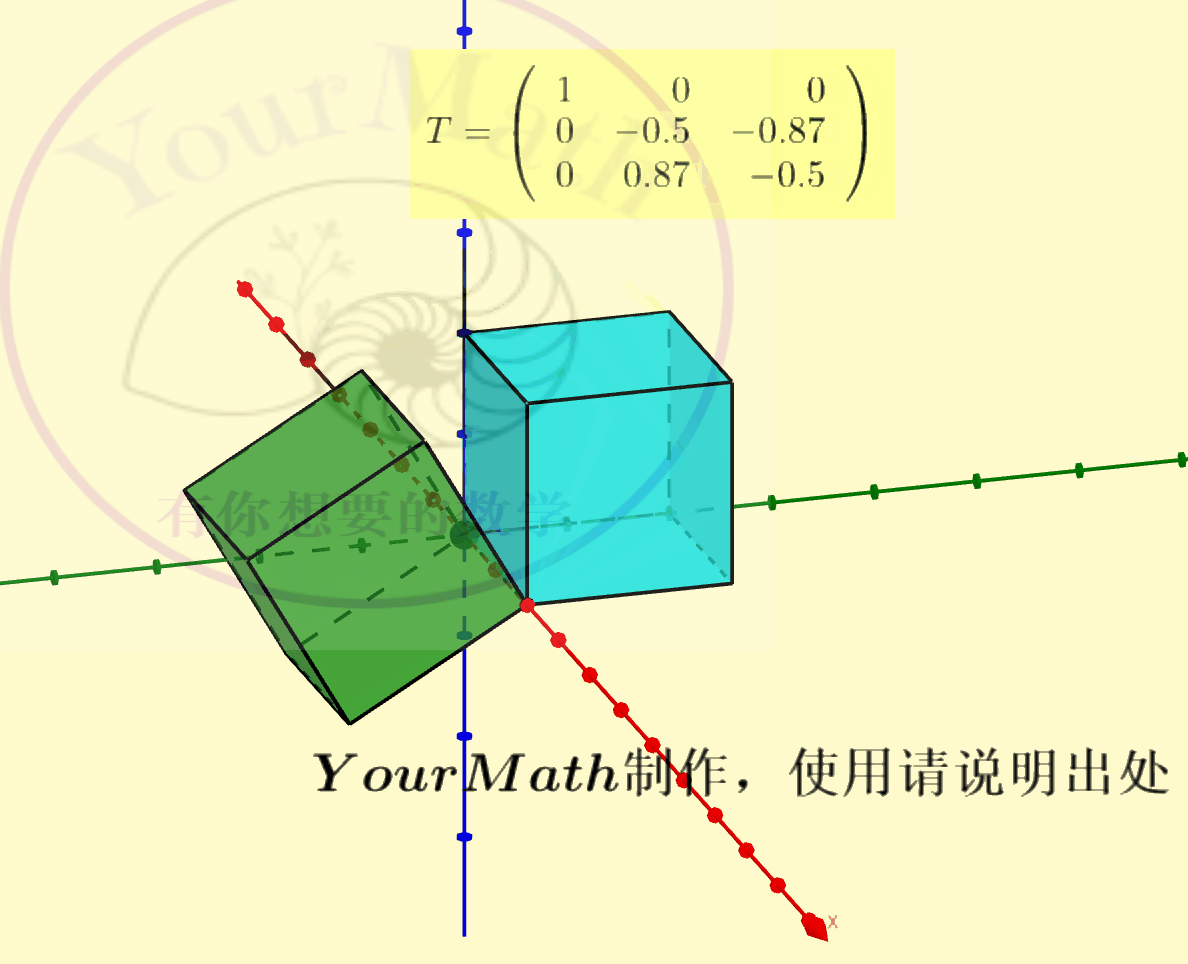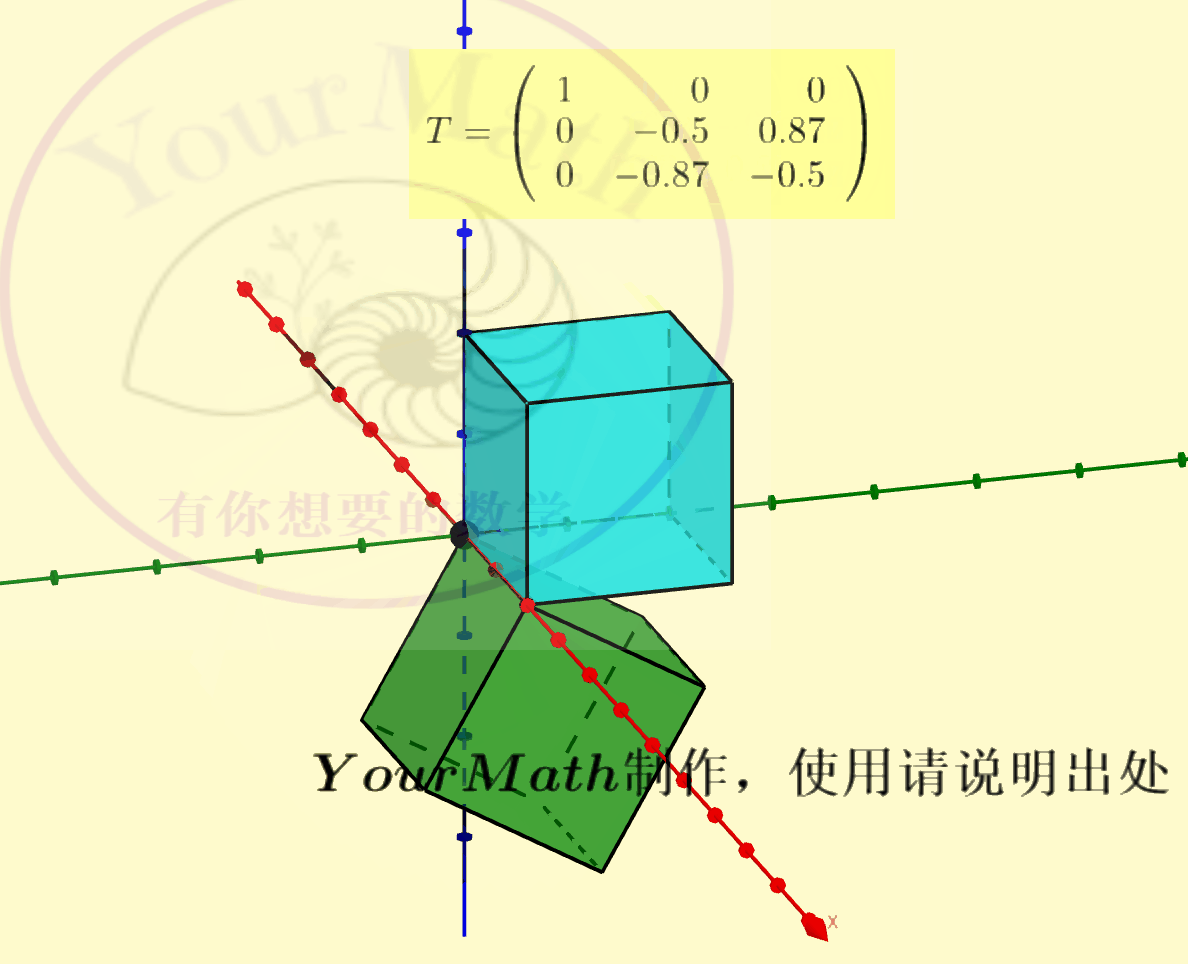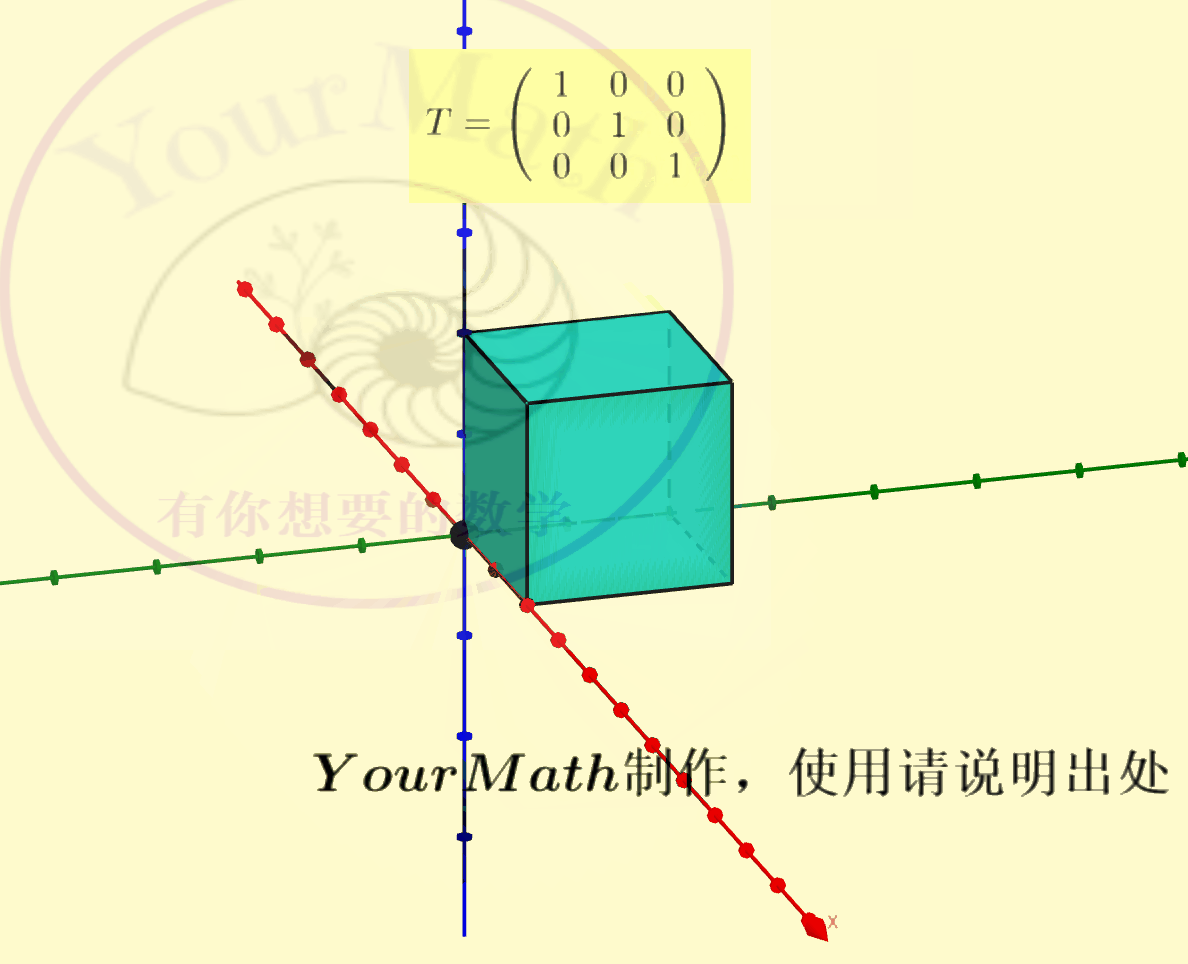
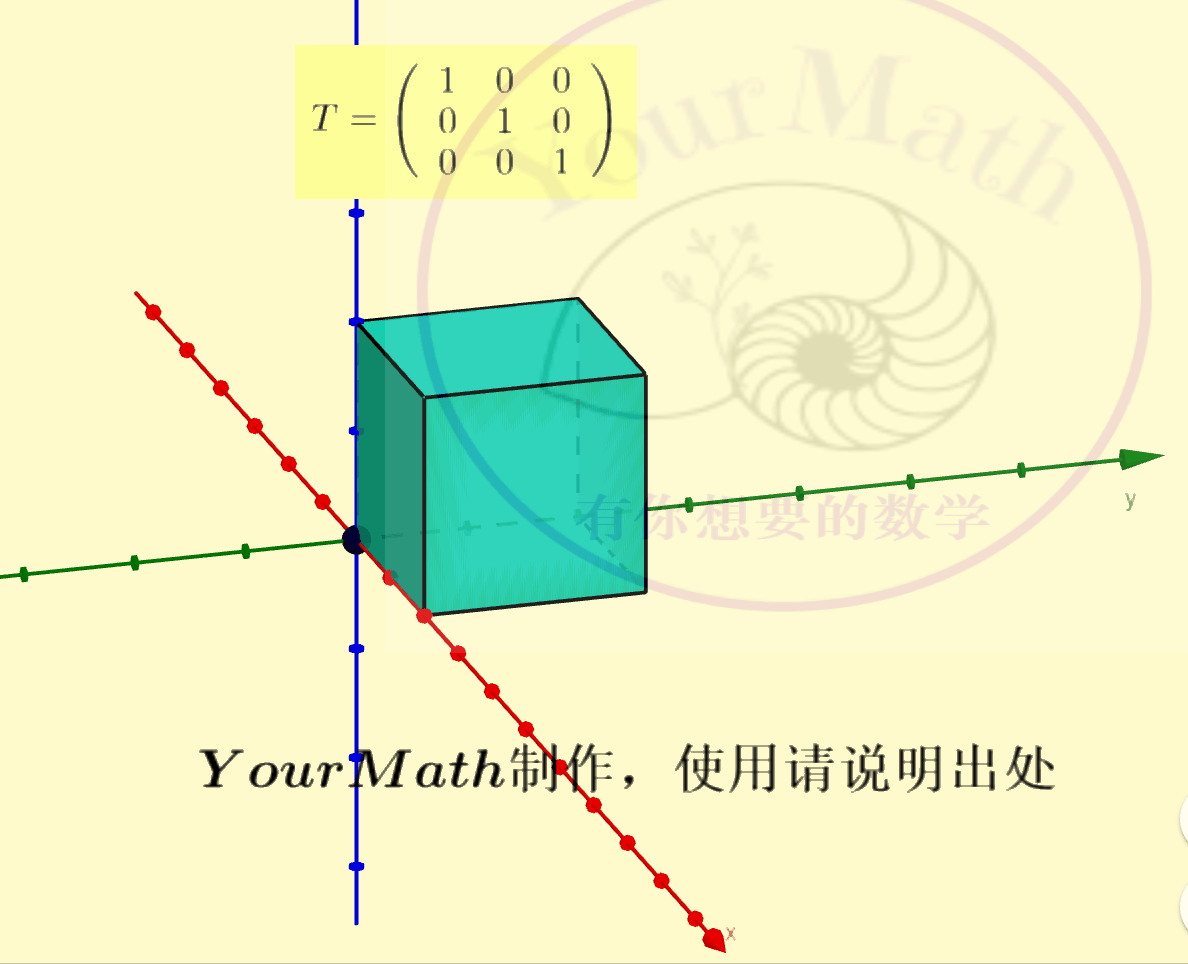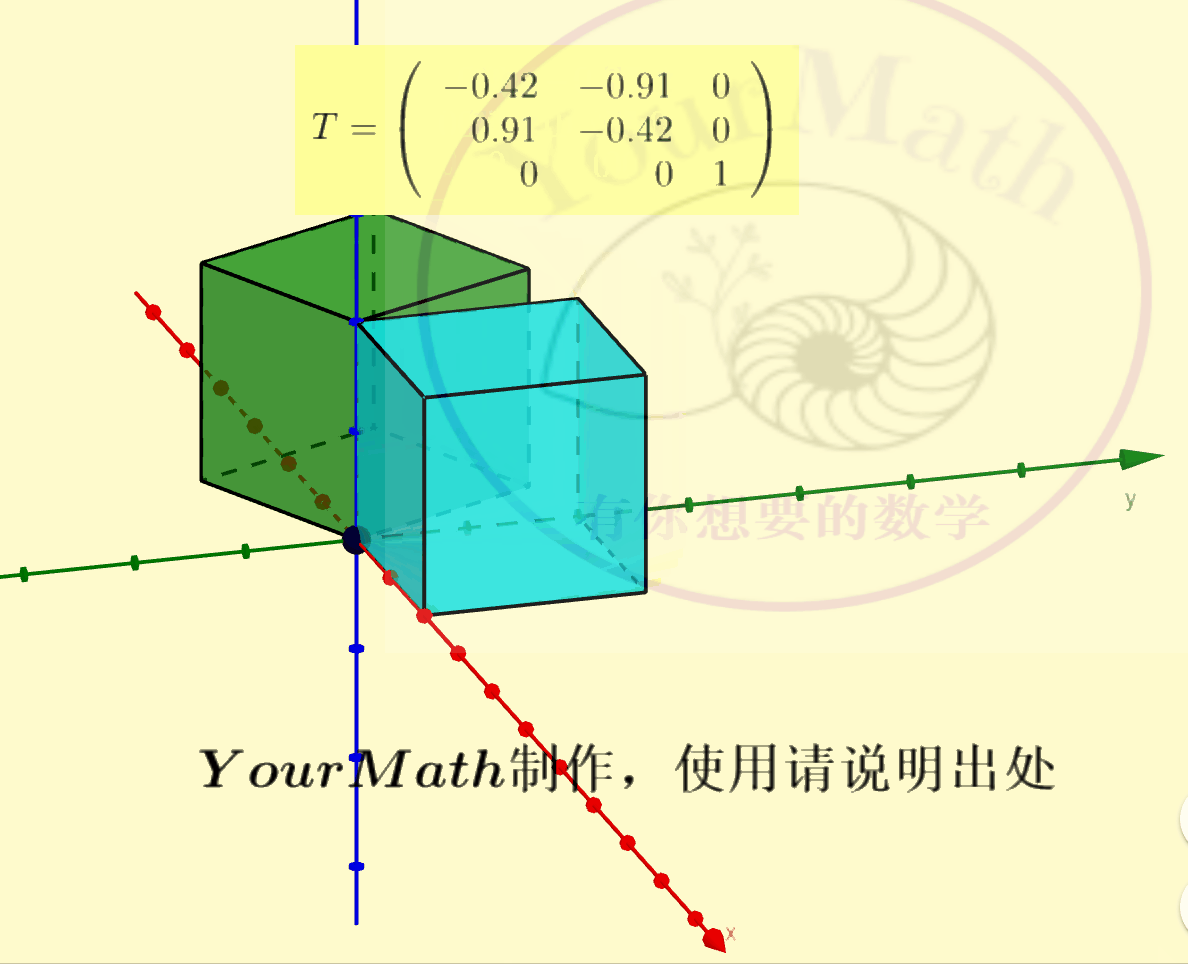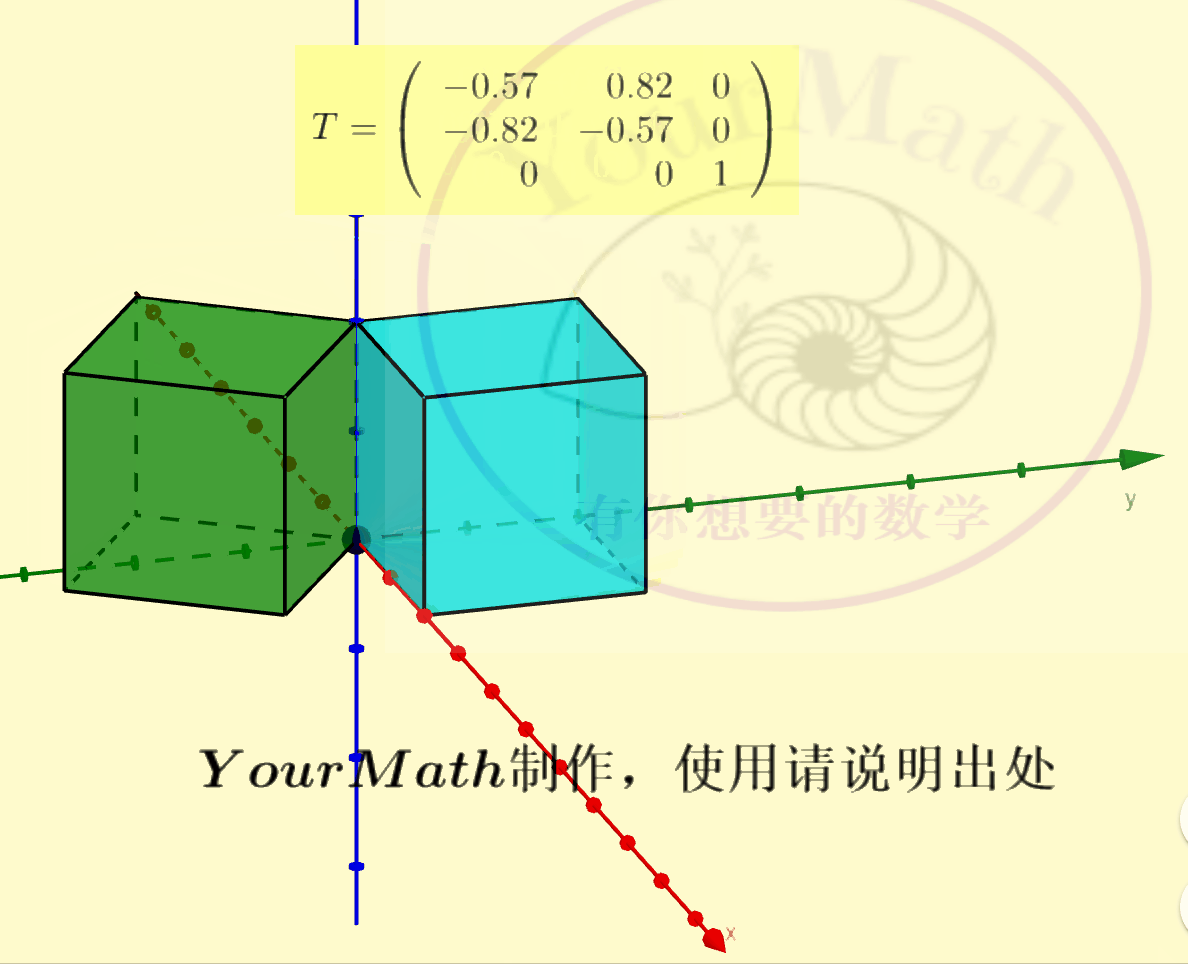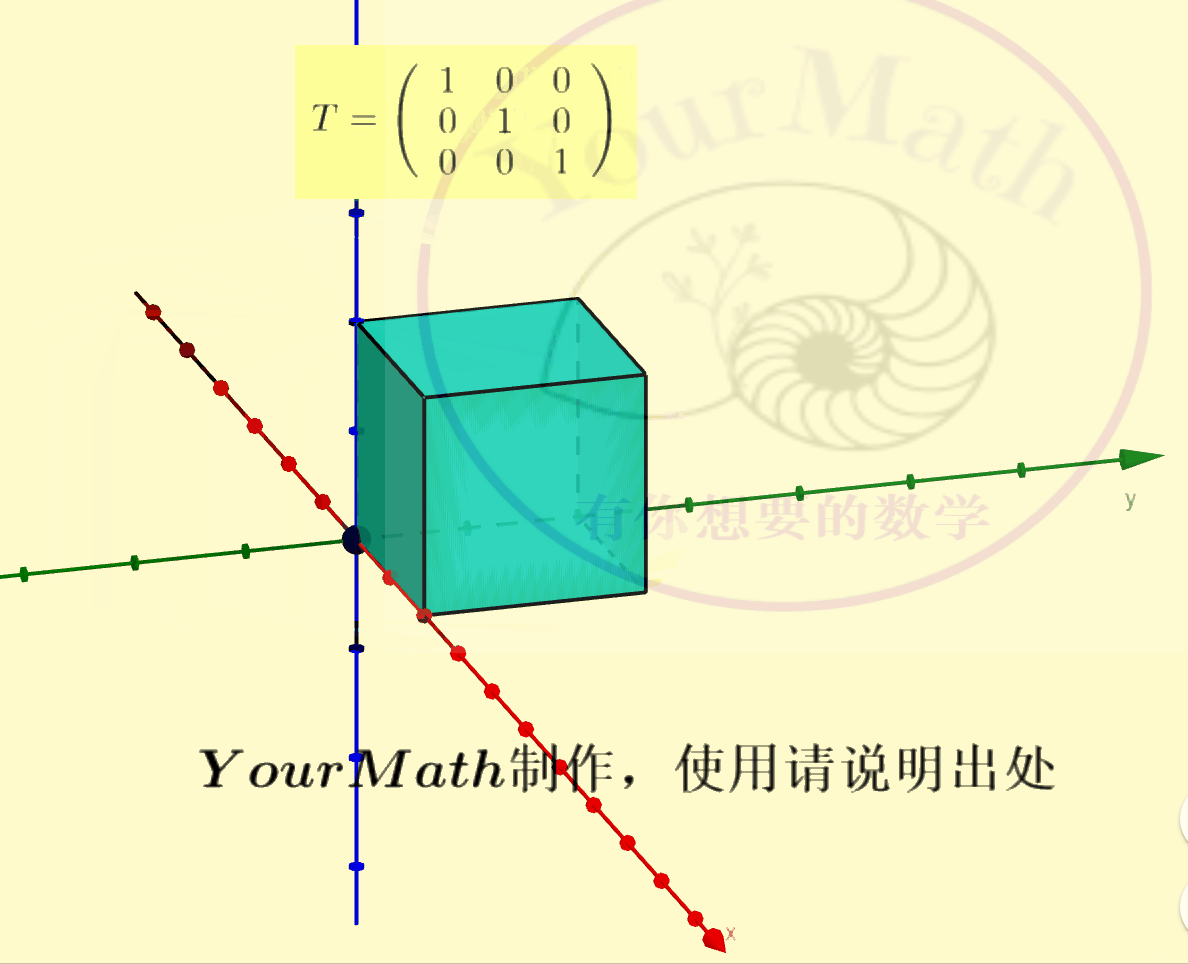
用右手系也可以轻松理解三维空间中坐标轴的旋转：

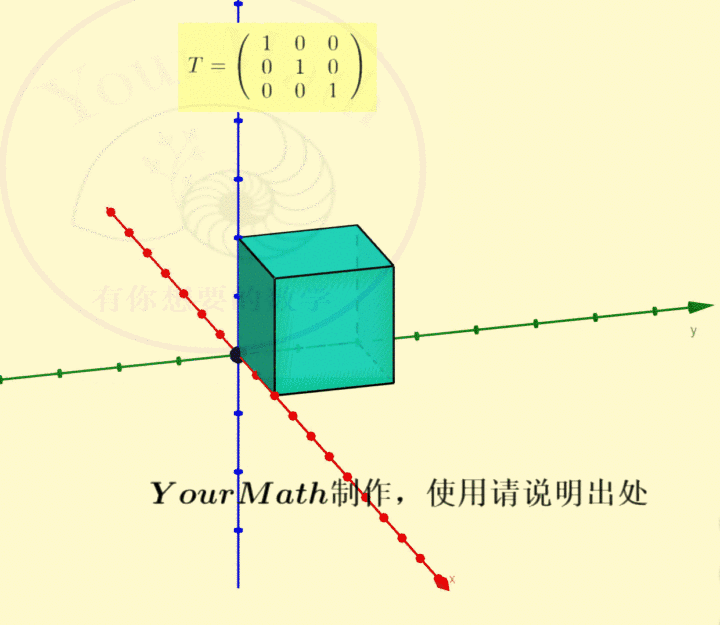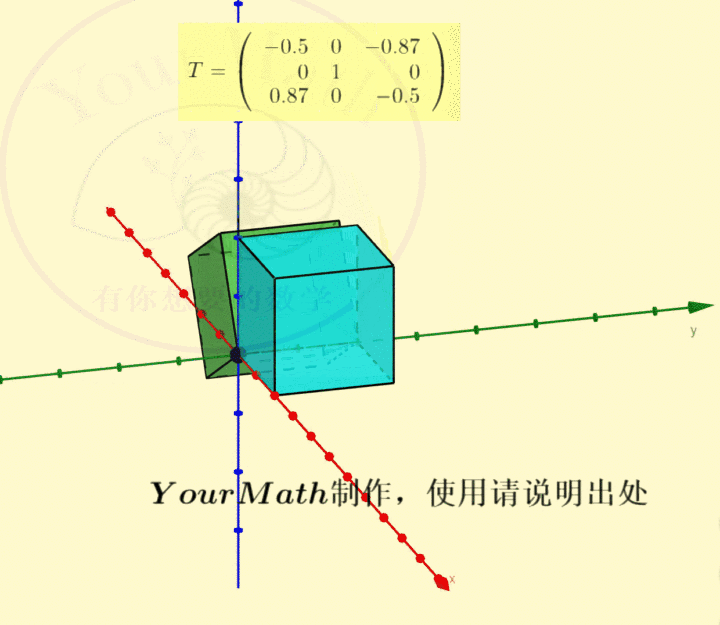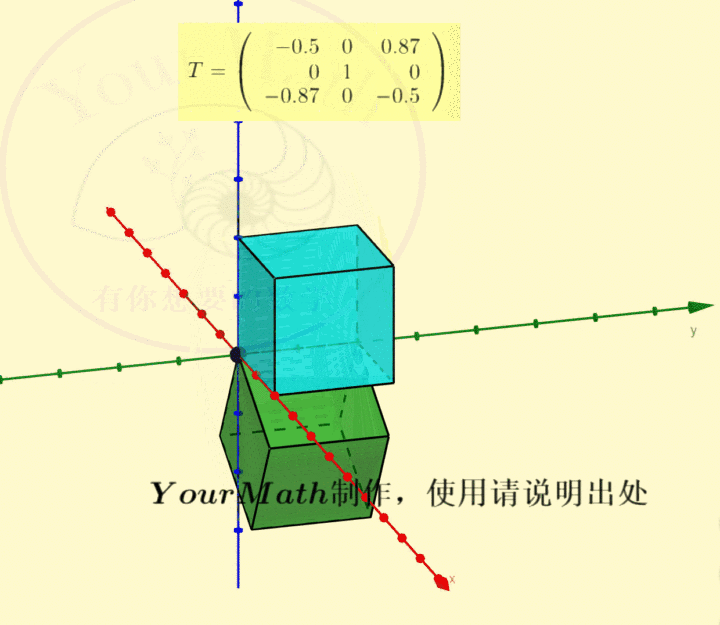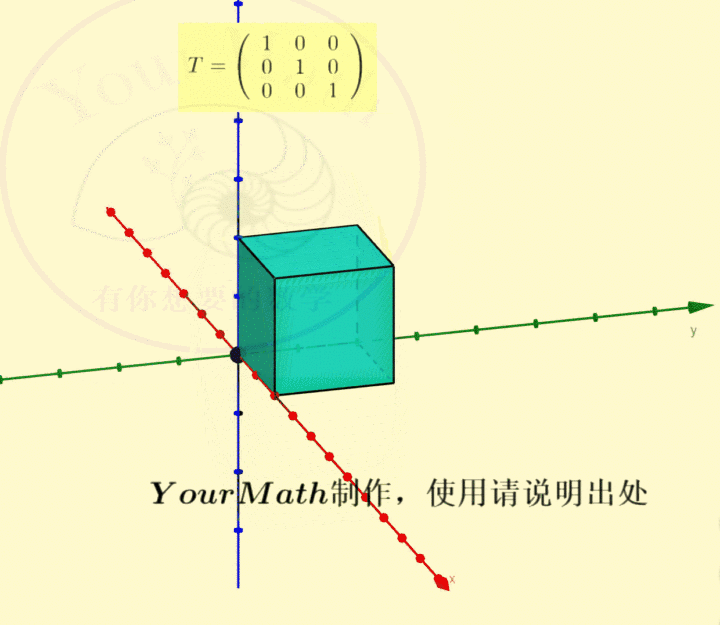
请欣赏三维空间中绕三个坐标轴的旋转的正交变换对应的正交矩阵

绕x-轴旋转

绕y-轴旋转

绕z-轴旋转

绕某个向量旋转

实际上，三维空间中的旋转变换有很多应用，比如欧拉角：欧拉角包括绕

轴，

轴和

轴的3个旋转，分别称为Pitch(俯仰)，Yaw（偏航）和Roll(翻滚)，如下图(图片来自网络)

更多内容大家可以自行搜素欧拉角、旋转角、或者四元数。