本文探讨了稀疏光流在目标追踪中的应用，通过利用少量特征点的局部亮度变化，解释了如何基于泰勒展开求解位移。同时，对比了与稠密光流的差异，后者使用更多像素点进行计算。关键在于理解亮度恒定假设和泰勒展开在光流估算中的作用。
稀疏光流
光流用在目标追踪过程中，基于上一帧的位置，预测目标在下一帧的位移；，如下图所示，我们需要求取的是像素点的位移u,v;
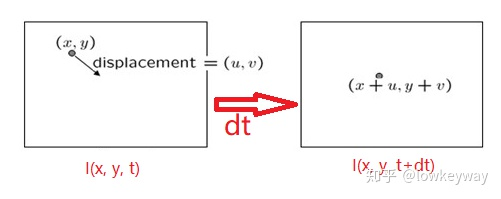
该预测基于的先验条件如下：
1.上一帧跟当前帧拍摄的时差较小，物体的位移不大；
2.某点像素（待检测目标上）周围的像素与该点具有相同的位移；
3.亮度恒定，上一帧与当前帧的变化不大；
根据亮度恒定假设，我们可以得到：
I
(
x
,
y
,
t
)
=
I
(
x
+
d
x
,
y
+
d
y
,
t
+
d
t
)
I(x,y,t)=I(x+d_{x},y+d_{y},t+d_{t})
I(x,y,t)=I(x+dx,y+dy,t+dt)
根据时差比较小，我们将右边进行泰勒展开，可以得到：
I
(
x
,
y
,
t
)
=
I
(
x
,
y
,
t
)
+
∂
I
∂
x
d
x
+
∂
I
∂
y
d
y
+
∂
I
∂
t
d
t
I(x,y,t)=I(x,y,t)+\frac{\partial I}{\partial x}{d_{x}}+\frac{\partial I}{\partial y}{d_{y}}+\frac{\partial I}{\partial t}{d_{t}}
I(x,y,t)=I(x,y,t)+∂x∂Idx+∂y∂Idy+∂t∂Idt
可以得到
∂
I
∂
x
d
x
+
∂
I
∂
y
d
y
+
∂
I
∂
t
d
t
=
0
（
2
）
\frac{\partial I}{\partial x}{d_{x}}+\frac{\partial I}{\partial y} {d_{y}}+\frac{\partial I}{\partial t}{d_{t}}=0 （2）
∂x∂Idx+∂y∂Idy+∂t∂Idt=0（2）
具体步骤：
1.在上一帧中目标所在的区域内提取N个特征点；
2.在每个特征点周围划取5*5的像素大小块patch m;(为什么要划取一个块？因为单个点的像素不具有表征特征，单个点的特征是由它周围的一小块区域来表征的）；可以得到公式2，两个变量，一个公式是求解不出来的，基于一个点去求解也不可靠，25个点就有25个公式，可以依据最小二乘法求解最佳的u,v
稠密光流
稀疏光流在上一帧检测出来的目标区域内利用若干个特征点计算位移；
扫一扫
546
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
