304 Range Sum Query 2D - Immutable

最新推荐文章于 2024-08-08 07:21:37 发布

weixin_39145266

最新推荐文章于 2024-08-08 07:21:37 发布

阅读量72

点赞数

CC 4.0 BY-SA版权

分类专栏： LeetCode # Medium # DynamicProgramming # Solved

本文链接：https://blog.youkuaiyun.com/weixin_39145266/article/details/93745291

LeetCode 同时被 3 个专栏收录

200 篇文章

订阅专栏

Medium

178 篇文章

订阅专栏

Solved

160 篇文章

订阅专栏

本文介绍了一种高效算法，用于解决二维矩阵中任意子矩阵元素之和的问题。通过预处理构建一个辅助矩阵，实现快速查询，避免了每次求和时重复计算，大大提高了效率。

1 题目

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

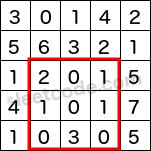
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

Note:

You may assume that the matrix does not change.
There are many calls to sumRegion function.
You may assume that row1 ≤ row2 and col1 ≤ col2.

2 尝试解

2.1 分析

问题303的升级版，给定一个二维整数矩阵matrix，求其中任何一个子矩阵内整数之和。可以直接将待求区域的整数相加，但是复杂度为O（mn），与待求区域面积成正比。用一个与matrix同样大小的矩阵怎sum_from_topleft记录从左上角到每一个位置构成的矩阵内整数之和。则sumRange(row1,col1,row2,col2) = sum_from_topleft(row2,col2)+sum_from_topleft(row1,col1)-sum_from_topleft(row1-1,col2)-sum_from_topleft(row2,col1-1)。

2.2 代码

class NumMatrix {
public:
    NumMatrix(vector<vector<int>>& matrix) {
        sum_from_topleft = matrix;
        for(int i = 0; i < matrix.size();i++){
            for(int j = 0; j < matrix[i].size();j++){
                sum_from_topleft[i][j] = matrix[i][j]-(i>0&&j>0?sum_from_topleft[i-1][j-1]:0)+(i>0?sum_from_topleft[i-1][j]:0)+(j>0?sum_from_topleft[i][j-1]:0);
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return sum_from_topleft[row2][col2]-(row1>0?sum_from_topleft[row1-1][col2]:0)-(col1>0?sum_from_topleft[row2][col1-1]:0)+(row1>0&&col1>0?sum_from_topleft[row1-1][col1-1]:0);
    }
private:
    vector<vector<int>> sum_from_topleft;
};

3 标准解

class NumMatrix {
private:
    int row, col;
    vector<vector<int>> sums;
public:
    NumMatrix(vector<vector<int>> &matrix) {
        row = matrix.size();
        col = row>0 ? matrix[0].size() : 0;
        sums = vector<vector<int>>(row+1, vector<int>(col+1, 0));
        for(int i=1; i<=row; i++) {
            for(int j=1; j<=col; j++) {
                sums[i][j] = matrix[i-1][j-1] + 
                             sums[i-1][j] + sums[i][j-1] - sums[i-1][j-1] ;
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2+1][col2+1] - sums[row2+1][col1] - sums[row1][col2+1] + sums[row1][col1];
    }
};