超详解排序算法之（四）希尔排序

希尔排序

引入希尔排序

我们先看插入排序遇到的一种情况[插入排序可以出门左转，看上一篇内容]，假定有一个数组[2,3,4,5,6,1],我们用插入排序的时候，我们只是将1插入这个数组最前边就可以，但是我们之前需要一步步从3、4、5、6，才能操作我们最终定序的这个1，这个1我们依次向左每遇到一个数字就要前移一下。简单插入排序遇到的问题就是：当需要插入的数是较小的数时，后移的次数明显增多，对效率有影响。
希尔排序是对于简单插入排序的改进，也称为缩小增量排序。

希尔排序的基本思想

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，正儿文件恰被分成一组，算法便终止。

---

图解说明一下

代码实现

交换法结论代码

/**
* @param array 待排序的数组
*/
public static void shellSortByChange(int[] array){
	int temp=0;
	for(int step=array.length/2;step>0;step=step/2){
		for(int i=step;i<array.length;i++){
			for(int j = i-step;j>=0;j-=step){
				if(array[j]>array[j+step]){
					temp=array[j];
					array[j]=array[j-step];
					array[j-step]=temp;
				}
			}
		}
	}
}

分布代码详解实现

int temp=0;//声明一个标量作为临时变量进行交换处理

//第一轮 每组的步长为5
for(int i=5;i<array.length;i++){
	for(int j=i-5;j>=0;j-=5){//这儿才开始对于每一组开始做处理，通过步长从索引下标0开始
		if(array[j]>array[j+5]){
			temp = array[j];
			array[j]=array[i+5];
			array[j+5]=temp;
			}
	}
}
System.out.println("第一轮分组循环之后的情况"+ Arrays.toString(array));

// 第二轮 每组的步长为2
for(int i=2;i<array.length;i++){
	for(int j=i-2;j>=0;j-=2){//这儿才开始对于每一组开始做处理，通过步长从索引下标0开始
		if(array[j]>array[j+2]){
			temp = array[j];
			array[j]=array[i+2];
			array[j+2]=temp;
			}
	}
}
System.out.println("第二轮分组循环之后的情况"+ Arrays.toString(array));

// 第三轮 每组的步长为1
for(int i=1;i<array.length;i++){
	for(int j=i-1;j>=0;j-=1){//这儿才开始对于每一组开始做处理，通过步长从索引下标0开始
		if(array[j]>array[j+1]){
			temp = array[j];
			array[j]=array[i+1];
			array[j+1]=temp;
			}
	}
}
System.out.println("第三轮分组循环之后的情况"+ Arrays.toString(array));

归纳总结形成 "通项公式"

1. 我们通过对于原始序列不断进行二分进行分组，当分组之后的步长>0 的时候我们就继续分，知道步长为1做最后一轮的处理，即简单插入排序，我们用一个for循环获取步长：for(int step=array.length/2;step>0;step/=2)
   2.对于每一组，我们通过组内进行交换处理，即插入排序的处理，从每一组的第二个元素开始进行，第一个元素就是操作元素的下标-步长。
   /**
   * 对于步长为2的分析
   * step=2，外层的处理为分组的情况对于每一组从第二位开始
   *
   *
   */
   for(int i=step;i<array.length;i++){//即分别对每一组的第二个元素开始进行递增，每一组第2为、第3位。。。
   for(int j=i-step;j>=0;j-=step){//通过与上边的关系，获取对应的组从下标0、1,、2.。。开始的元素与前边元素的比较
   }
   }
   这的处理类似于选择排序的思想
   所以我们最终的归纳代码即为：

int temp=0;
int count=0;
for(int step = array.length/2;step>0;step/=2){
            for(int i=step;i<array.length;i++){
                for (int j = i-step; j >= 0; j-=step) {//j=i-step;j<array.length;j+=step
                    if(array[j]>array[j+step]){//array[j]<array[j-step]
                        temp=array[j];
                        array[j]=array[j+step];
                        array[j+step]=temp;
                    }

                }

            }
            //打印出每一次分组之后的排序结果
            System.out.println("第"+(++count)+"轮分组循环之后的情况"+ Arrays.toString(array));
        }

我们代码测试一下是否符合我们的分析的结果

说明我们的代码没有问题

---

上述的处理我们采用的是交换法，我们看看交换处理的效率怎么样
直接上代码和测试结果

public static void main(String[] args) {

        int[] arr = new int[80000];
        for (int i = 0; i < arr.length; i++) {
            arr[i]=(int)(Math.random()*800000);
       }
        System.out.println("希尔排序！！");

       Date dateStart = new Date();
        SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        System.out.println("Front of Execute:"+simpleDateFormat.format(dateStart));

       shellSort(arr);

       Date dateEnd = new Date();
        System.out.println("Front of Execute:"+simpleDateFormat.format(dateEnd));

结果

我们看到好像比插入排序还需要更长的时间，不是说希尔排序是对插入排序的改进么？越改越回去了？？小伙伴猜猜问题出在哪里？花点时间考虑一下哦。
下边就是答案了。

---

我们对于每一组内找到的内容都是进行交换处理的，这样的效率并不高，所以我们只需要将之前做交换的部分处理为插入的方式，我们再看看效率。具体的推导在此就不在赘述，如果有需要，请留言。看到会回复。

希尔排序移动法

public  static  void shellSort2(int[] array){
        int count=0;
        for(int gap=array.length/2;gap>0;gap/=2){//同样先分组
            //从第gap个元素，逐个对其所在的数据进行直接插入排序
            for(int i= gap;i<array.length; i++){
                int j=i;
                int temp = array[j];
                if(array[j]<array[j-gap]){

                    while(j - gap >=0 && temp < array[j-gap]){
                        array[j]=array[j-gap];
                        j-=gap;
                    }
                    //当跳出循环的时候，就表示找到了插入的位置
                    array[j]=temp;

                }

            }

            System.out.println("第"+(++count)+"轮分组循环之后的情况"+ Arrays.toString(array));
        }

    }

我们先验证一下我们这段代码的正确性
用同样的数据{8,9,1,7,2,3,5,4,6,0}，上结果

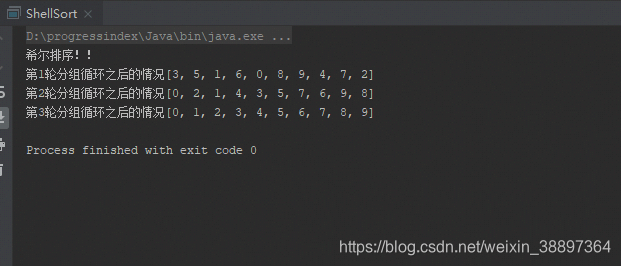
接着我们进行测试一把80000个数据的处理效率是否有提升

	public static void main(String[] args) {
        int[] arr = new int[80000];
        for (int i = 0; i < arr.length; i++) {
            arr[i]=(int)(Math.random()*800000);
        }
        System.out.println("希尔排序！！");

        Date dateStart = new Date();
        SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        System.out.println("Front of Execute:"+simpleDateFormat.format(dateStart));

        shellSort2(arr);

        Date dateEnd = new Date();
        System.out.println("Front of Execute:"+simpleDateFormat.format(dateEnd));

    }
    /**
     * 移动法
     * @param array
     */
    public  static  void shellSort2(int[] array){
        int count=0;
        for(int gap=array.length/2;gap>0;gap/=2){//同样先分组
            //从第gap个元素，逐个对其所在的数据进行直接插入排序
            for(int i= gap;i<array.length; i++){
                int j=i;
                int temp = array[j];
                if(array[j]<array[j-gap]){

                    while(j - gap >=0 && temp < array[j-gap]){
                        array[j]=array[j-gap];
                        j-=gap;
                    }
                    //当跳出循环的时候，就表示找到了插入的位置
                    array[j]=temp;

                }

            }

//            System.out.println("第"+(++count)+"轮分组循环之后的情况"+ Arrays.toString(array));
        }

    }

结果展示

秒级的处理，感兴趣的小伙伴可以将时间精度改为毫秒级，看下对应的处理速度，然后试试80W个数据的处理速度。希尔排序到此先告一段落。具体的时间依据个人电脑的状态可能有所不同，可以多测几次，平均值，80w条数据不到1s的时间吧。