排序算法 | 希尔排序 + Python实现

排序算法

在数据结构与算法中，常用的排序算法有如下6种：冒泡排序、选择排序、插入排序、快速排序、希尔排序以及归并排序。下面介绍第5种算法：希尔排序。

希尔排序

希尔排序（Shell Sort）是插入排序的一种，也称为缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 DL.Shell 于1995年提出而得名。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减少至1时，整个文件恰被分为一组，算法便终止。

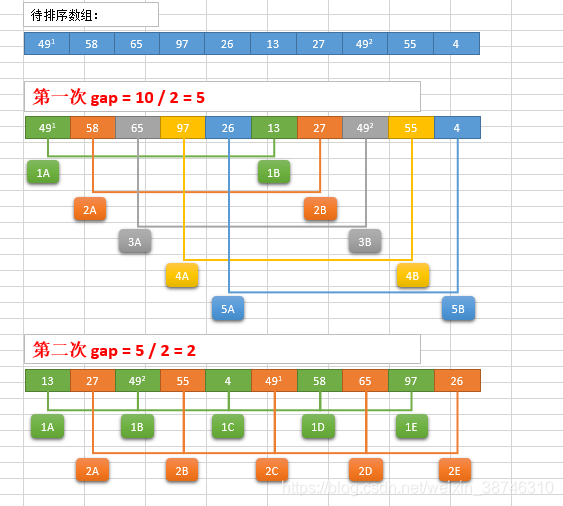
排序过程

希尔排序的基本思想是：将数组列在一个表中并对列分别进行插入排序，重复这一过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解算法，算法本身还是使用数组进行排序。

例如，假设有这样一组数[13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10]，如果我们以步长为 5 开始进行排序，我们可以通过将这列表放在有 5 列的表中更好地描述算法，这样他们就应该看起来是这样（竖着的元素时步长组成）：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]。这时10已经移至正确位置了，然后再以3为步长进行排序：

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之后变为：

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最后以 1 步长进行排序（此时就是简单的插入排序了）。
算法分析

Python 实现

def shell_sort(alist):
	n = len(alist)
	gap = n // 2
	while gap > 0:
		for j in range(gap, n):
			# j = gap, gap + 1, ... gap + n - 1
			i = j
			while i > 0:
				if alist[i] < alist[i-gap]:
					alist[i], alist[i-gap] = alist[i-gap], alist[i]
					i -= gap
				else: break
		gap //= 2	

时间复杂度

• 最优时间复杂度：根据步长序列的不同而不同
• 最坏时间复杂度：$O(n^2)$
• 稳定性：不稳定