UMAP：比t-SNE更好的降维算法

论文题目：UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction
作者：Leland McInnes； John Healy； James Melville
时间：December 7, 2018

UMAP (Uniform Manifold Approximation and Projection) 算法是一种创新的降维流形学习算法。Ideas 来自于拓扑数据分析。

1. 论文整体思路

• UMAP uses local manifold approximations and patches together their local fuzzy simplicial set representations to construct a topological representation of the high dimensional data.
• a similar process can be used to construct an equivalent topological representation.
• then minimize the cross-entropy between the two topological representations.

2. 背景补充

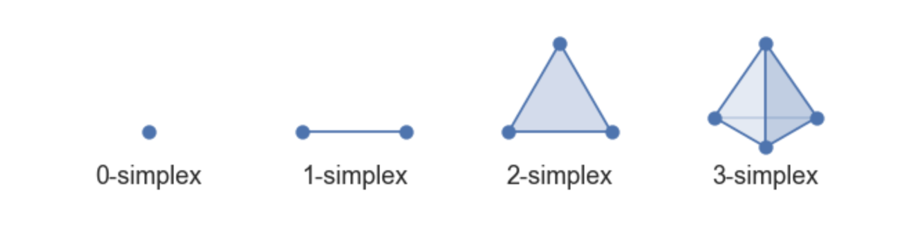
单纯形 (Simplices)

从几何上讲，单纯形是构建 k 维对象的一种非常简单的方法。 k 维单纯形称为 k-单纯形。它是由𝑘+1个独立点的凸包构成的。因此，0-单纯形是一 个点，1-单纯形是一条线段 (在两个零单纯形之间)，2-单纯形是一个三角形 (其中三个1-单纯形作为“面”)，而3-单纯形是一个四面体 (四个2-单纯形作为“面”)。

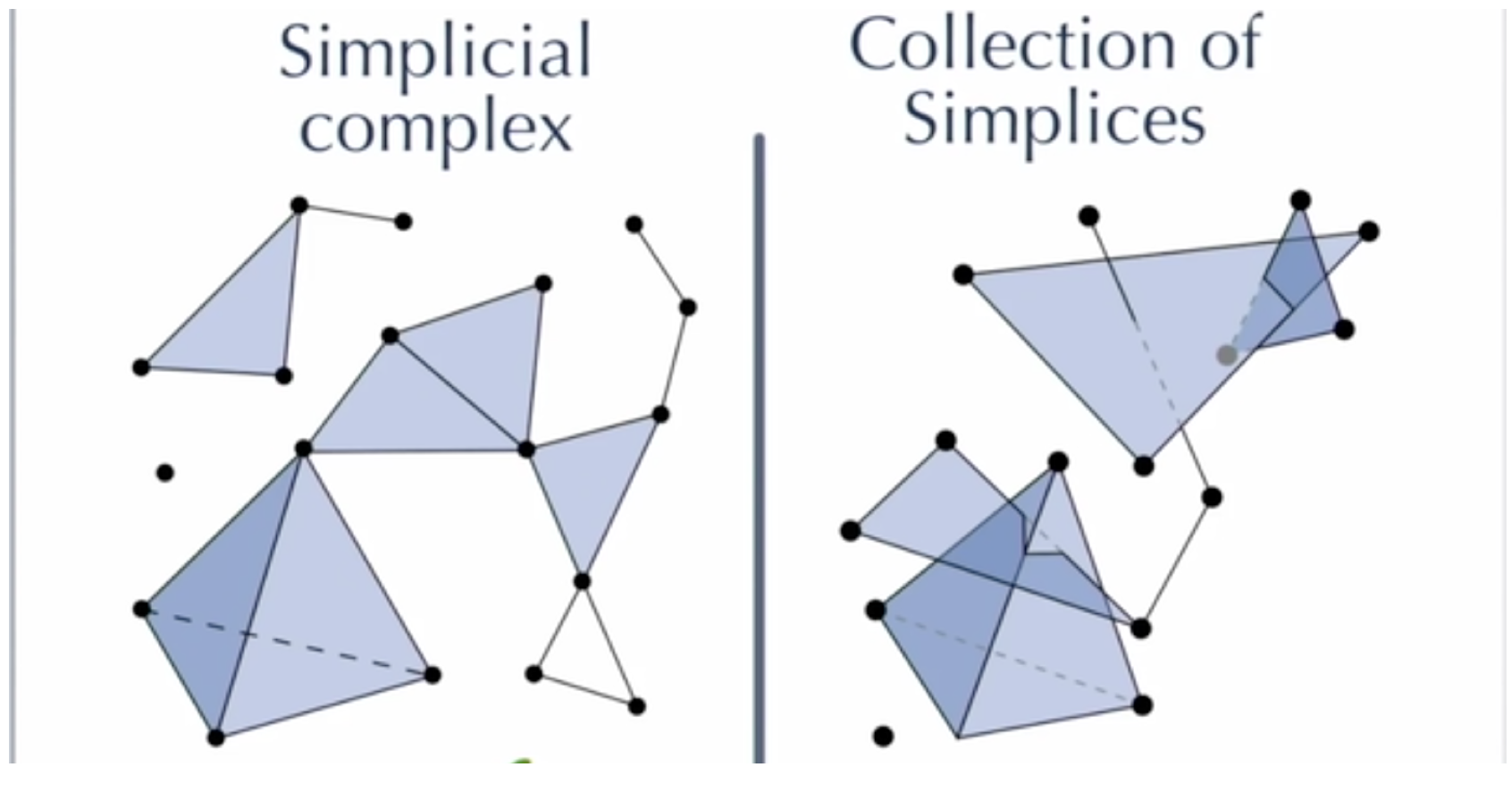
单纯复形 (Simplicial complex)

A simplicial complex $K$ is a set of simplices that satisfies the following conditions:

1. Every face of a simplex from $K$ is also in $K$.
2. The non-empty intersection of any two simplices $\sigma _{1},\sigma _{2}\in K $ is a face of both $ \sigma_1,\sigma_2$.

(The convex hull of any nonempty subset of the n + 1 points that define an n-simplex is called a face of the simplex. )

单纯复形 K 是单纯形的集合。任意单纯形的任何面也在 K 中(确保所有面都存在)，并且 K 中任何两个单纯形的交集都是这两个单纯形的面。

3. 理论应用

假设一个有限的数据样本集来自一个拓扑空间，如果要了解该空间的拓扑，需要先生成该空间的开覆盖 (open cover)。

若数据实际处于 metric space，一种近似开覆盖的方法是对每个数据点形成固定半径的球。

举例，有一批数据位于假设的流形中。如图所示：

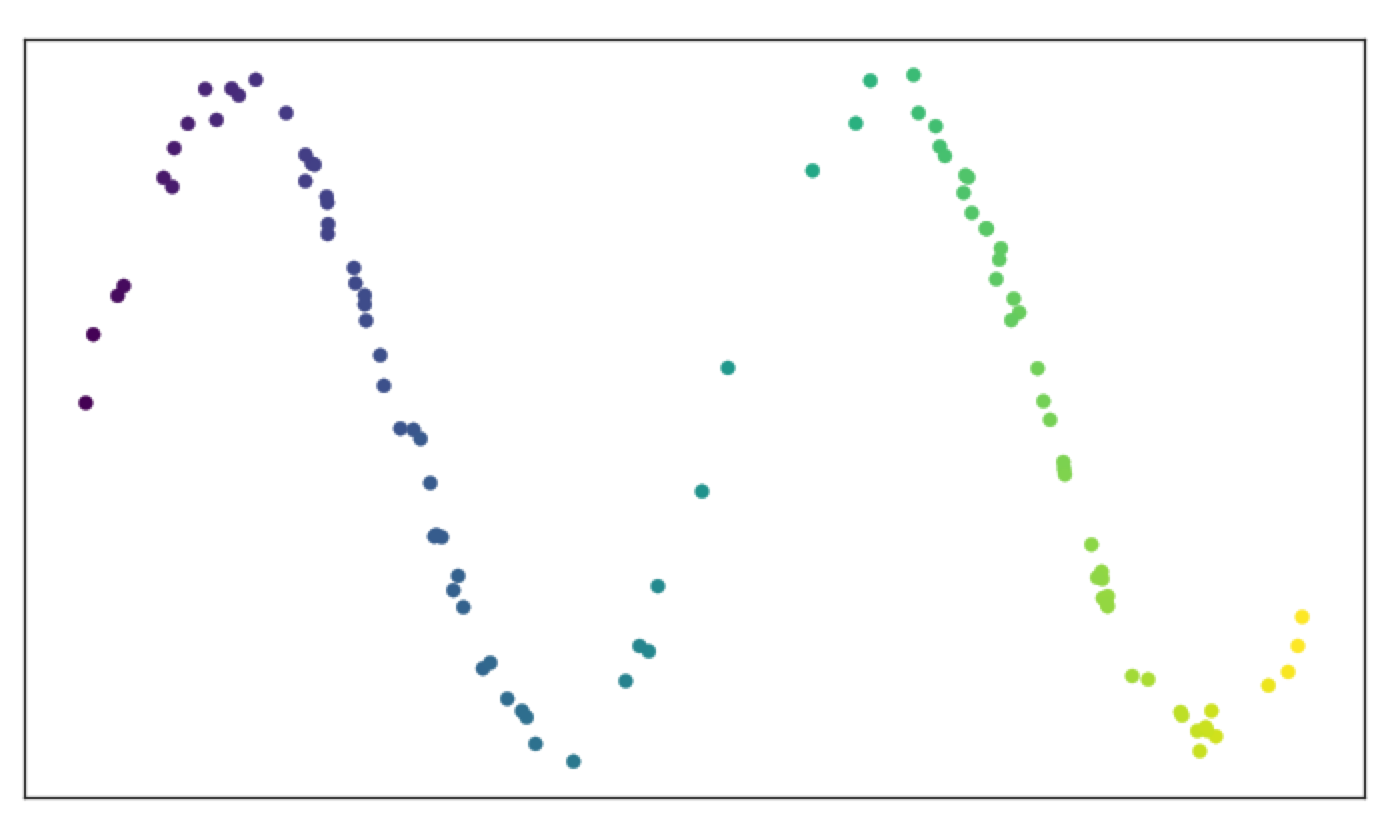
如果固定一个半径，就可以把覆盖的开放集想象成一个个圆（考虑二维）。

构造单纯复形。 具体是指构造Čech 复形。

具体方法是：

让覆盖 (cover) 中的每个集合都是0-单纯形；如果两个集合具有非空交集，则在它们之间创建1-单纯形；如果三个这样的集合的三重交集都非空，则在集合之间创建2-单纯形；以此类推。

然后，我们可以将0-、1-和2-单纯形的单纯复形描绘为点、线和三角形。如图所示：

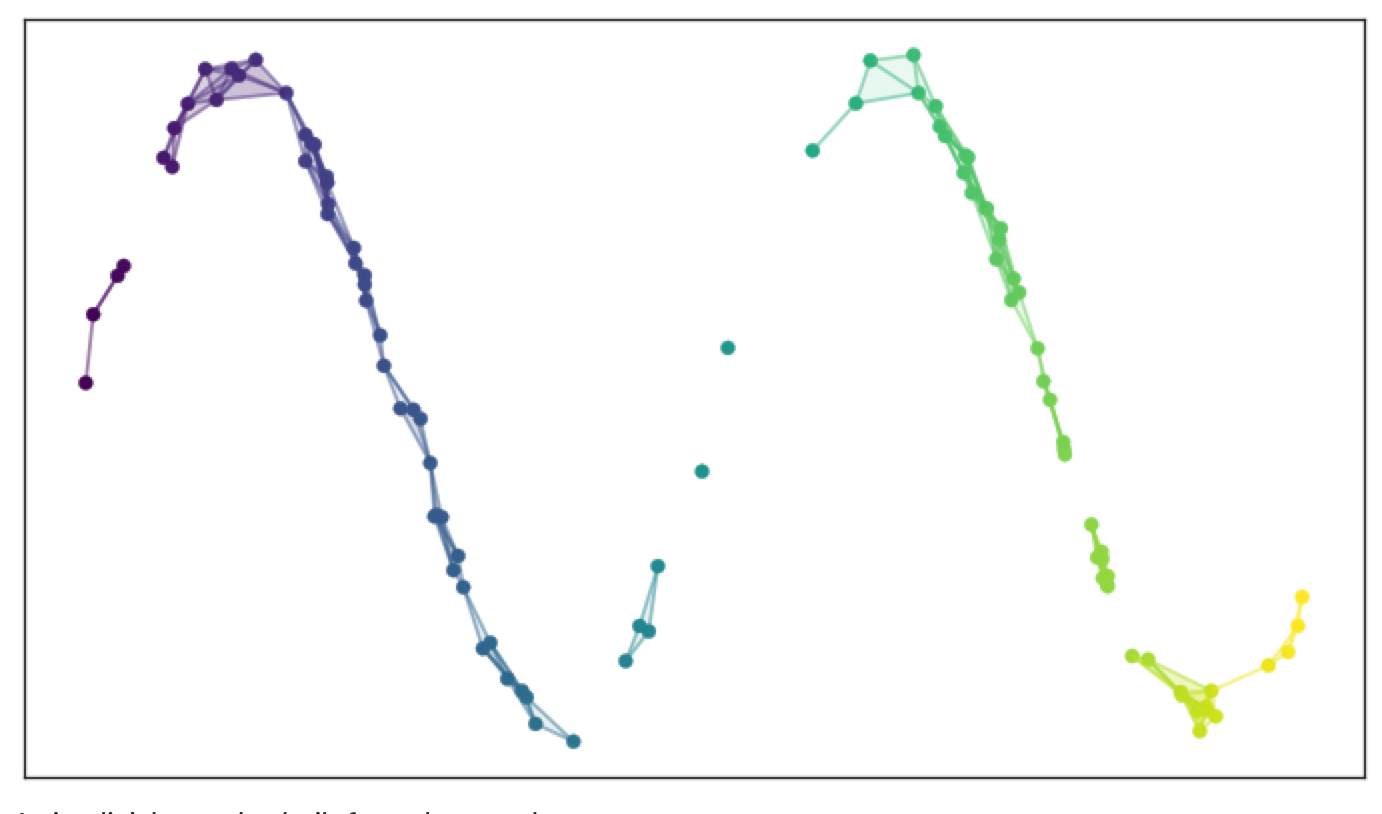
通过这样的方法捕获拓扑结构。

4. 一些改进

理论可行，但在实际数据上的效果不佳。

问题1：如何为开覆盖选择正确的球半径？

半径太小 —> 单纯复形分裂为许多相连的组件。
半径太大 —> 单纯复形变成维度很高的单纯形，无法捕捉流形结构。

解决方案：

Assumption: Data is uniformly distributed on the manifold.

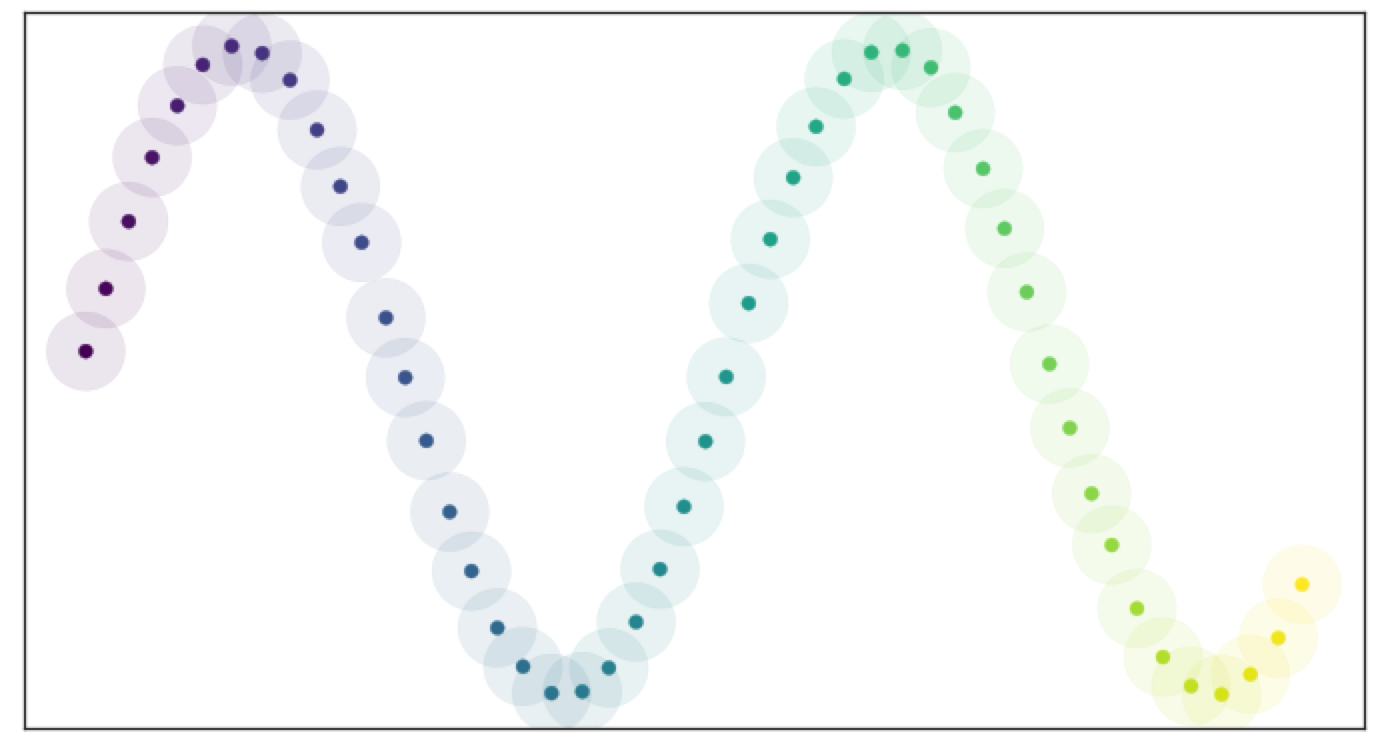
数据在流行上均匀分布，就不难选择一个好的半径。

数据均匀分布的假设在流形学习的其他地方也有。比如：拉普拉斯映射要证明有效，就要假设数据是均匀分布的。

但是，现实中的数据不会是均匀分布的。问题反过来：假设数据均匀分布在流形上，我们能得到关于流形的什么信息？

即：距离的概念在流形上是不一样的 - 空间扭曲：在数据看起来更稀疏或更密集的地方来拉伸或缩小。

引入黎曼几何。
在流形上定义一个 Riemannian metric 让假设为真。
在黎曼空间里数据点是均匀分布的，但是放到欧几里得空间就变成非均匀分布了。

球的大小在不同的度量下是不一样的。在黎曼度量下球的 size 是一样的，但放在欧几里德空间就不一样了。

通过假设数据是均匀分布的，可以通过使用一些标准的黎曼几何来计算每个点的局部距离概念(其近似值)。围绕一个点的单位球延伸到该点的第 k 个最近的邻居，其中 k 是我们用来近似局部距离的样本大小。

每个点都有自己唯一的距离函数，我们可以简单地选择半径为1的球作为局部距离函数！

于是我们发现这不就是 k-近邻图吗？

这意味着数据集中的每个点都被赋予了到其k个最近邻居的每个点的边-这是我们使用半径为1的球的局部变化度量的有效结果。

对 k 的拓扑解释，k 的选择决定了我们希望在多大程度上局部地估计黎曼度量。选择很小的k意味着我们想要一个非常局部的解释，它将更准确地捕捉到黎曼度量的精细细节结构和变化。选择较大的 k 意味着我们的估计将基于更大的区域，可以有更多数据来估计。

基于黎曼度量的另一个好处

我们实际上有一个与每个点相关联的局部度量空间，并且可以有意义地测量距离，因此可以根据边上的点之间的距离(根据局部度量)来加权可能生成的图的边。

用模糊拓扑的知识来理解：在一个覆盖的开集合不再是是和否的概念，而是介于 0 和 1 的模糊值。点在给定半径的球里的确定性会随着我们离开球的中心的移动而衰减。我们可以把这样一个模糊的 cover 想象成如图所示的样子：

问题2：更高的维度上的数据很多点是完全孤立的。

解决方法：局部连接。

Assumption:
The manifold is locally connected.

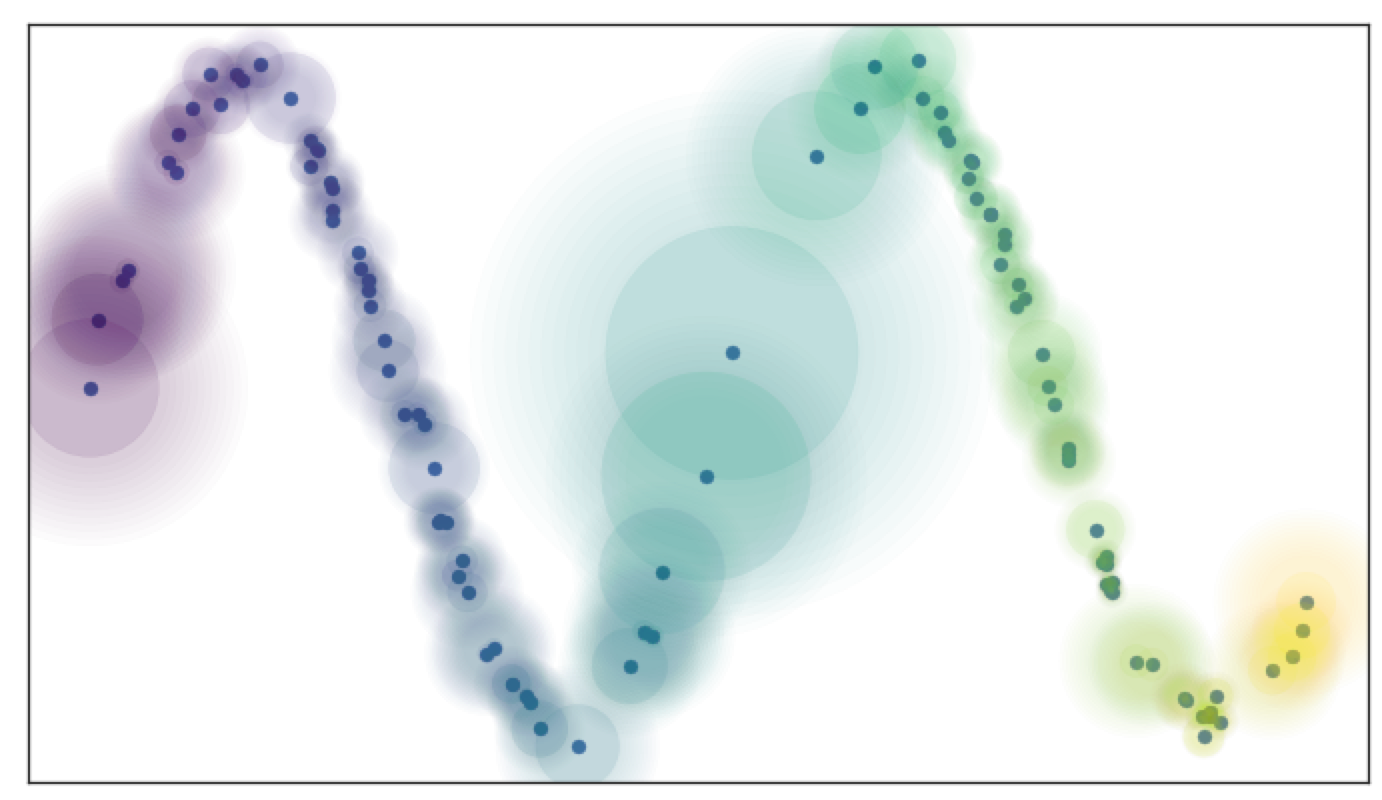
由于维数诅咒，高维空间的数据，距离更大，但彼此也可能更相似。这意味着到第一个最近邻居的距离可能相当大，但到第十个最近邻居的距离通常只会稍微大一点(相对而言)。局部连接的约束确保我们关注最近邻居之间的距离差异，而不是绝对距离(这显示邻居之间的差别很小)。

问题3：局部度量标准不兼容性。

每个点都有与其相关联的局部度量，并且从点a的角度来看，从点a到点b的距离可能是1.5，但是从点b的角度来看，从点b到点a的距离可能只有0.6。

基于图形的直觉，可认为这是具有不同权重的有向边，如下图所示：

解决方法：

将权重为 a 和 b 的两条不一致的边合并在一起，那么我们应该有一条具有组合权重 $a+b-a\cdot b$的边。考虑这一点的方法是，权重实际上是边 (1-单纯形) 存在的概率。然后，组合权重是至少一条边存在的概率。

如果我们应用这个过程将所有模糊单纯集合并在一起，我们最终得到一个单一的模糊单纯复合体，我们可以再次将其视为一个加权图。在计算方面，我们只是将边权重组合公式应用于整个图 (非边的权重为0)。最后，我们得到了类似这样的东西。

因此，最终只是构造了一个加权图。但是背后有强大的数学知识在支撑。

因此，假设我们现在有了数据的模糊拓扑表示 (数学上说它将捕获数据背后的流形的拓扑)，我们如何将其转换为低维表示呢？

找到一个低维表示

目的：希望低维表示具有尽可能相似的模糊拓扑结构。
第一个问题是如何确定低维表示的模糊拓扑结构;
第二个问题是如何找到一个好的拓扑结构。

第一个问题可遵循以上寻找数据模糊拓扑结构的过程。

数据位于的流形是我们试图嵌入的低维欧几里德空间。因此，流形上的距离是相对于全局坐标系的标准欧几里得距离，不再是变化的度量。

第二个问题，“如何找到一个好的低维表示”，即衡量模糊拓扑结构的匹配程度，最终可以转化为一个优化问题。

采用的优化方法是交叉熵函数。

回顾之前的权重处理方法，我们将权重解释为单纯形存在的概率。由于我们正在比较的两个拓扑结构共享相同的0-单纯形，可以想象我们正在比较由1-单纯形索引的两个概率向量。假设这些都是伯努利变量 (最终单纯形要么存在，要么不存在，而且概率是伯努利分布的参数)，这里正确的选择是交叉熵。

如果所有可能的 1-单纯形的集合是 $E$，并且有权重函数使得 $w_h(e)$ 是高维情况下 $e$的权重， $w_l(e)$ 是低维情况下 $e$ 权重，则交叉熵是：

$$\sum _{e\in E}{w}_h(e)log(\frac{w_h(e)}{w_l(e)})+(1-w$$