softmax

1.softmax函数

                 

                       

 

任何数，当其通过softmax函数后，便映射到（0,1）上，我们可以视之为概率

等同于一个简单的映射，其中隐含层等同于一个全连接层。 

其中多分类，即选取输出向量中概率最大的前k个

2.相关求导

梯度下降：每次优化一个step大小的梯度，这个时候我们就要求Loss对每个权重矩阵的偏导，然后应用链式法则

常用交叉熵作为损失函数：

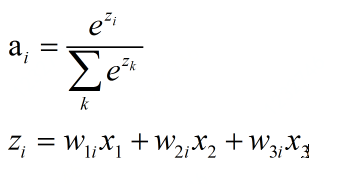
其中y指代真实值，a指代softmax求出的值。i代表网络的节点号，也是对应的label（Yi），如果仅仅预测i=1（猫）时，其余的节点的softmax输出为0，例如a1=5,a2=0,a3=0等。

若要预测第j个数据，则有（累和已经去掉了），若,那么形式变为

 

我们可得Loss是关于a(j)的函数，a(j)是关于z(j)的函数，z(j)是关于w(j)的函数。

若我们要让Loss函数求偏导传递到节点4，则有：

 

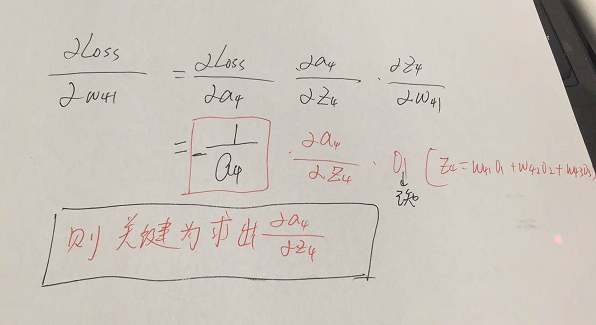
由上图可得，我们想得到，其余的求导是已知的，则我们对进行求导，则有，

j=i对应例子里就是如下图所示：

比如我选定了j为4，那么就是说我现在求导传到4结点这,节点4的前项传播过程如下：

有，，它的导数为,与上面相乘为 

这时对的是j不等于i，往前传：

则有，，它的导数为,与上面相乘为

 

举个栗子：

通过若干层的计算，最后得到的某个训练样本的向量的分数是[ 2, 3, 4 ], 那么经过softmax函数作用后概率分别就是=[,,] = [0.0903,0.2447,0.665]

若实际样本为第二类，那么，计算出来的偏导就是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]  （由于正确类时，loss的偏导为aj-1），然后进行反向传播。