本文探讨了在机器学习中遇到的常见问题，包括样本不均衡、过拟合和欠拟合。提出了如SMOTE、下采样、上采样、增加惩罚项权重等解决不平衡数据的方法。对于过拟合，可通过降低模型复杂度、增加数据集、正则化等手段来改善。欠拟合则需要提高模型复杂度、减小正则化项。此外，文章还介绍了稀疏性在模型中的重要性，以及为何在卷积神经网络中使用卷积和池化。
1.样本不均衡问题
1）增少：
SMOTE算法：简单来说smote算法的思想是合成新的少数类样本，得到少数样本A的最近邻中随机样本B，取AB连线的随机点合成
下采样
2）减多
随机欠抽样方法：上采样
3）增加样本惩罚项权重
2.过拟合问题？
1)降低模型复杂度
2)增大数据集
3）数据清洗
4)正则化项（即增加惩罚度，L0(非零参数个数)，L1（元素绝对值之和）,L2范数（各个参数平方和的开方））
为什么L0和L1都可以实现稀疏，但常用的为L1？L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解
5）Dropout层进行随机丢弃
6）早停
3.欠拟合问题？
1）提高模型复杂度
2）减小正则化项系数
3）加入新的特征
3.什么叫稀疏？参数稀疏有什么好处？
稀疏解即只在某（几）个轴上有实数，另外的轴为0 ，
1）例如模型参数中很多w=0，那么模型变得简单，不易过拟合
2）特征自动选择，会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为0
3）可解释性，非0参数越少，公式表达能力越强。(即越简单的结构表达能力越强)
4.为什么使用卷积？（从卷积特点上回答）
1）参数共享：即卷积核的参数是共享的。一个卷积核，如果它适用于一幅图片的左上角做边缘检测，则他也能适用于图片的右下角
2）稀疏连接:卷积输出的每一个数值（像素），只与卷积核大小内像素有关，与卷积核范围之外的其它像素无关
3）计算参数的数目，只和过滤器的维度大小和个数有关（不受图片大小的影响）
4）想提取更多的特征，只需要用不同参数的过滤器进行相同操作的卷积即可。（滤器参数的选择不同，我们就可以得到不同的特征检测器：例如sorbel垂直算子，水平算子等）。
栗子：两个不同的3×3*3的过滤器，得到两个4×4的输出，它们堆叠在一起，形成一个4×4×2的立方体，这里的2的来源于我们用了两个不同的过滤器。也就相当于我们对原始6*6*3图像提取了2个不同的特征
5.池化作用？
1）保留显著特征、降低特征维度，增大kernel的感受野
2）减少模型参数数量，缓解过拟合问题
3）满足全连接岑定长输入的需求（池化可以在不改变维度情况下使得特征图大小变化）
4)平移不变性：即使图像经历了一个小的平移之后，依然会产生相同的 (池化的) 特征
6.反向传播目的？ 它的推导？
目的：梯度下降法利用损失函数对所有参数的梯度，寻找局部最小值点
首先有：
上标表示网络层，下标表示神经元：
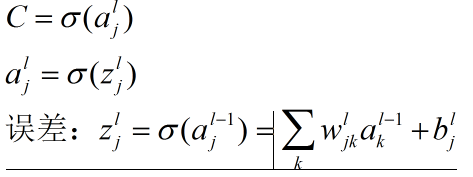
例如：softmax中有：
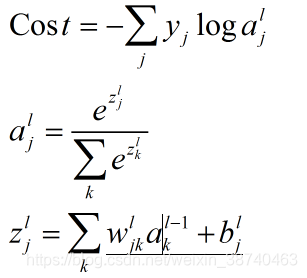
7.为什么要使用激活函数？ 常见的激活函数？
1）加入非线性因素，加强网络表达能力（若不使用激活函数，则每一层输出都是上层输入的线性组合，会失去神经网络的万能近似性），因此激活函数近似于非线性的传感器。
Relu：
优点：1）无梯度消散
2）负输入，输出为0， 增大网络的稀疏性
缺点： 1）当学习率较大时，反向传播中w可能为负，在经过rule函数，致使该层死亡
sigmoid 与 tanh ：
tanh(z)&nbs
最低0.47元/天 解锁文章
扫一扫
506
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
