文章目录
1 二叉树的遍历
1.7.1 二叉树的递归遍历
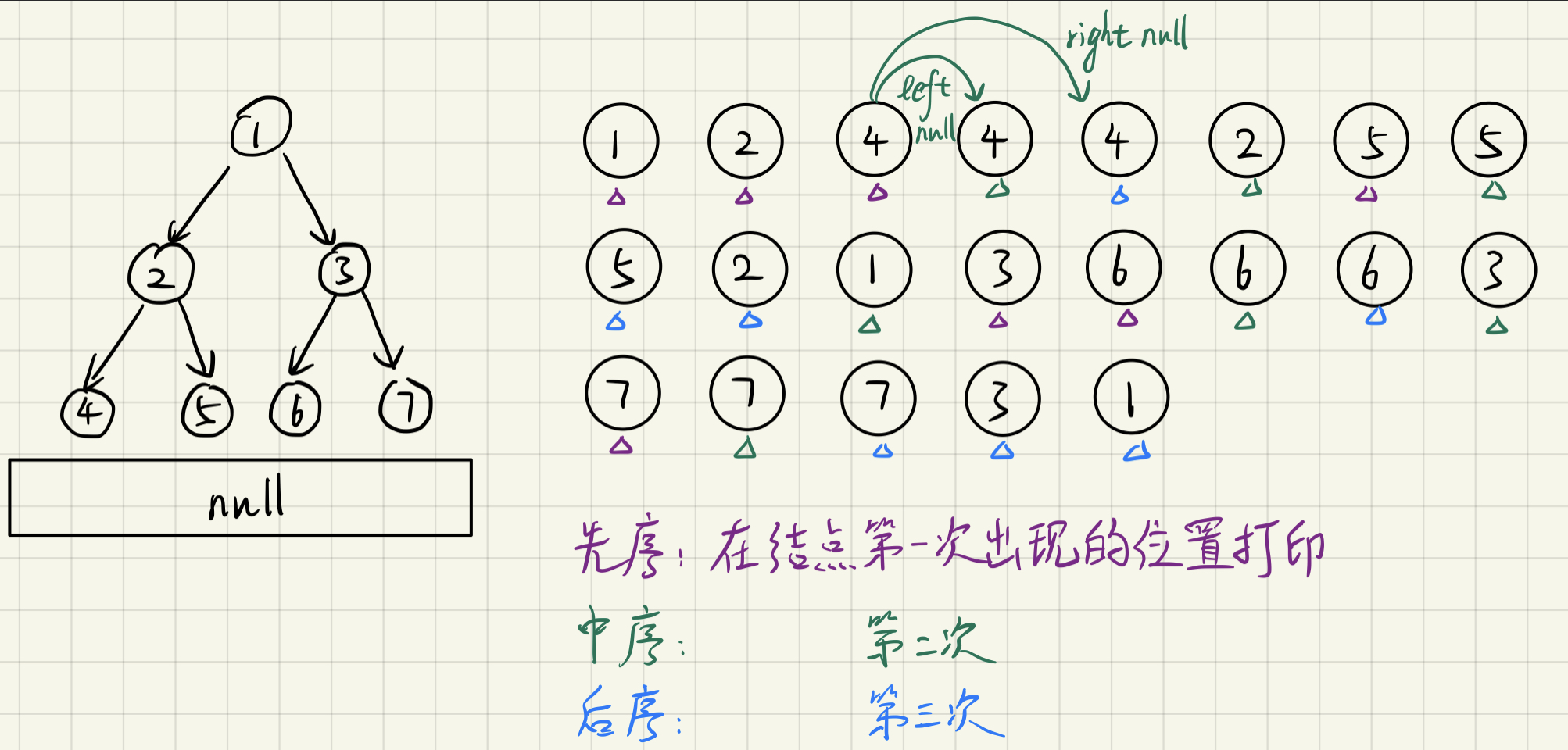
1.7.2 二叉树的非递归遍历
栈:为什么用栈:
栈是一个可以反向输出的结构,因为二叉树的遍历一定是从上往下遍历每一个节点,是单向的,但是在递归中,子节点遍历完后可以返回父节点,形成了反向的遍历,这时候选择栈结构比较合适。而且递归本身就是一个方法栈。
先序遍历:
算法:
- 准备一个栈
- 将头节点压进去
- 弹出头节点,打印,如果有的话,将右节点压入,再将左节点压入
- 如果最后一个元素弹出,且没有新的节点加入,说明遍历完成,栈已空
public static void preOrderNoRecur(Node head){
if (head != null){
Stack<Node> stack = new Stack<>();
Node cur = head;
stack.push(cur);
while(!stack.isEmpty()){
cur = stack.pop();
System.out.print(cur.value+" ");
if (cur.right!=null){
stack.push(cur.right);
}
if (cur.left!=null){
stack.push(cur.left);
}
}
}
}
中序遍历:
算法:
-
如果栈不为空或者当前节点不为null,开始执行
-
如果当前节点不为null:不停的将该节点的left 节点压栈,直到当前节点为null
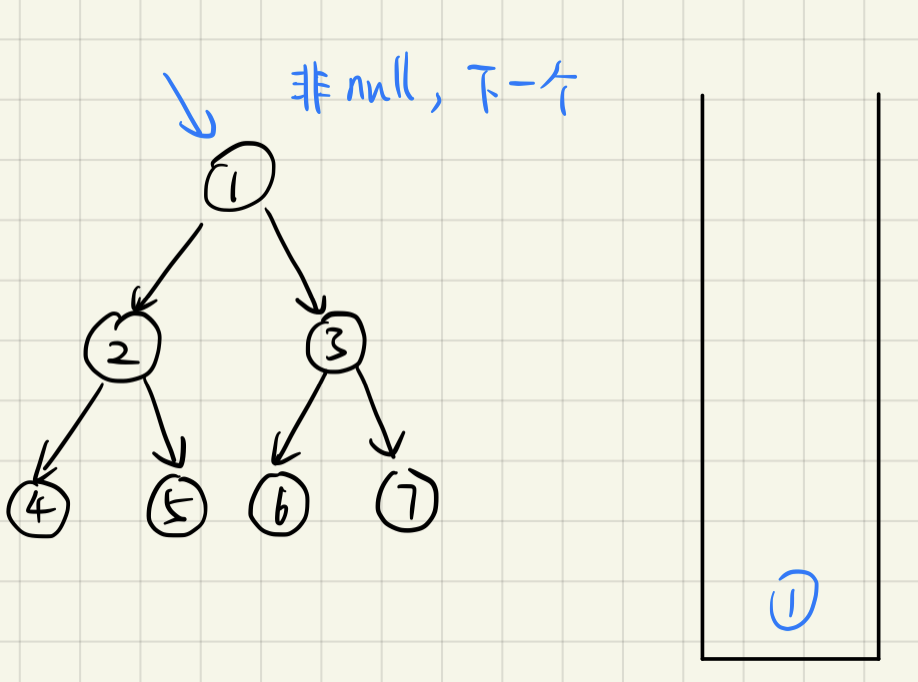
-
如果当前节点为null,但是stack不为空,开始弹栈,当前节点为弹出的节点,打印
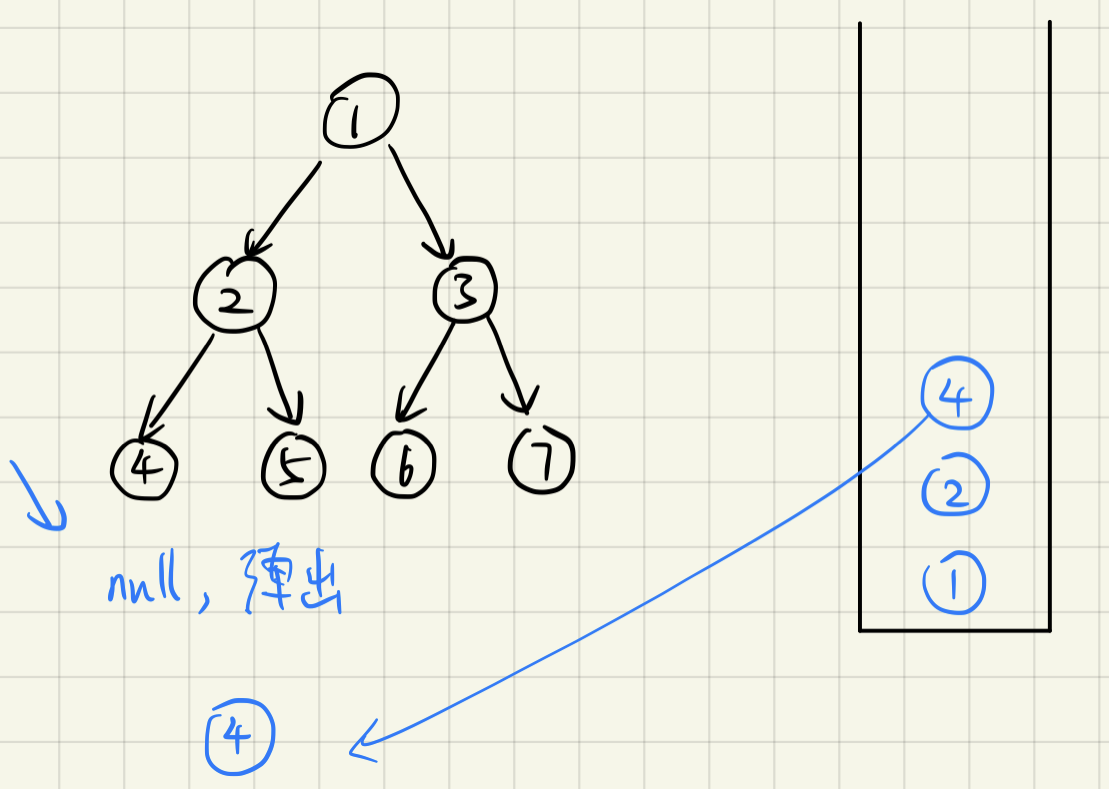
-
当前(如果当前节点有right子节点)节点变为right子节点
-
直到栈为空且当前节点为空,终止
public static void inOrderNoRecur(Node head){
if (head!=null){
Stack<Node> stack = new Stack<>();
Node cur = head;
while(!stack.isEmpty() || cur != null){
//如果当前节点不为空,一直将当前节点和左子节点
if (cur!=null){
stack.push(cur);
cur = cur.left;
}else {
cur = stack.pop();
System.out.print(cur.value+" ");
cur = cur.right;
}
}
}
}
直观逻辑:
-
将包括当前节点在内的左边树全部压入栈中–>压入完成
-
弹出栈顶元素,如果这个元素有右子节点,将包括右子节点在内的,以右子节点为首的左边树压入栈中–>压入完成
-
继续弹出栈顶元素
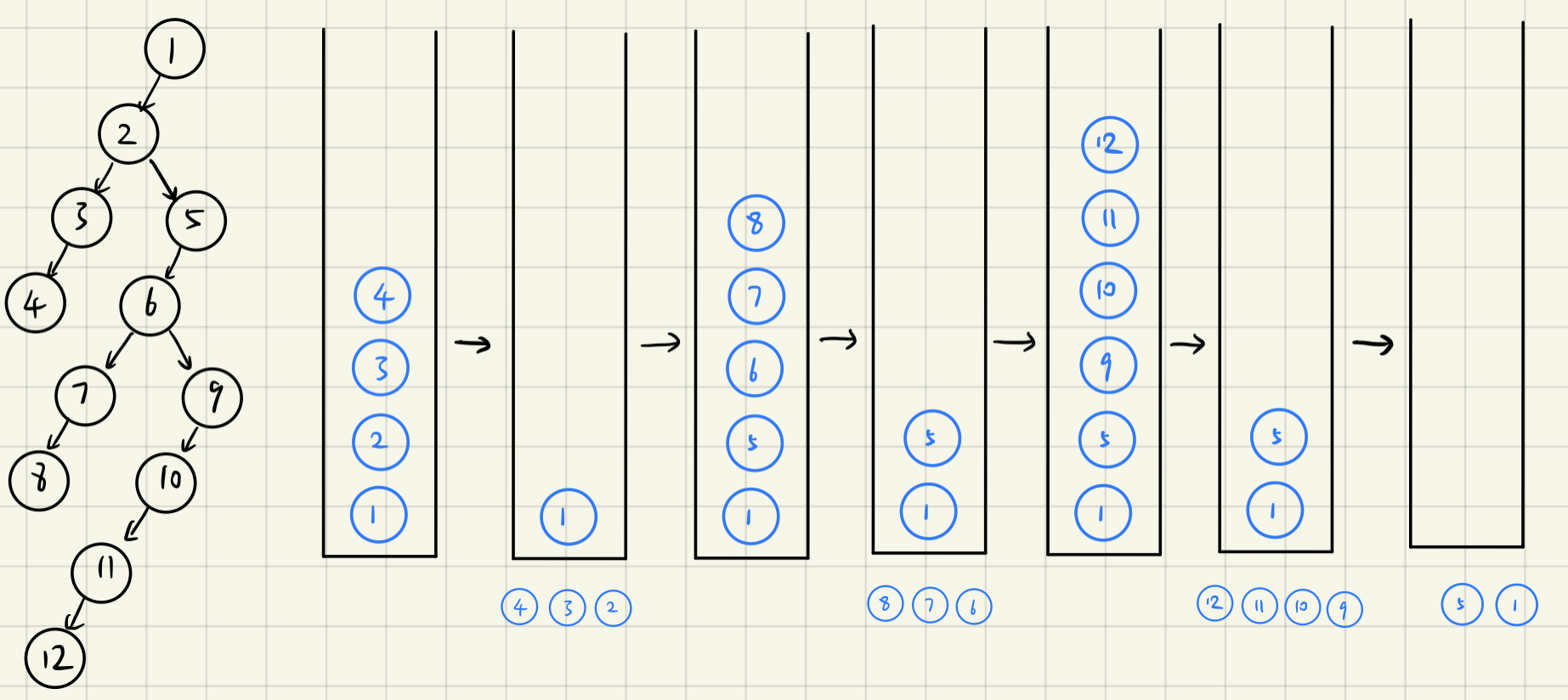
后序遍历
算法:
用两个栈,实现相反的先序遍历
- 考虑到:在先序遍历中,首先会pop头节点,然后将右节点和左节点压栈(因为栈会反向输出,所以输出顺序为左-右)
- 如果将输出变为压入另一个栈,pop头节点后,将先将左节点压栈,再压右节点,之后弹出的时候顺序就为右-左
- 所以会以中-右-左的顺序压入第二个栈
- 遍历第二个栈,就会以左-右-中的方式弹出
public static void posOrderNoRecur(Node head){
if (head != null){
Stack<Node> stack1 = new Stack<>();
Stack<Node> stack2 = new Stack<>();
Node cur = head;
stack1.push(cur);
while(!stack1.isEmpty()){
cur = stack1.pop();
stack2.push(cur);
if (cur.left!=null){
stack1.push(cur.left);
}
if (cur.right!=null){
stack1.push(cur.right);
}
}
while(!stack2.isEmpty()){
System.out.print(stack2 .pop().value+" ");
}
}
}
2.0 打印一棵二叉树
2.1 寻找二叉树的后继节点和前驱节点
2.2 二叉树的序列化和反序列化
序列化即是将二叉树的节点变成字符串,而且后期可以恢复回来
2.2.1 通过先中后序遍历将节点都序列化
用相同的方式来反序列化
2.2.2 通过层序遍历将节点序列化
2.3 判断一棵树是平衡二叉树
对于任何一个节点,如果左子树的高度和右子树的高度差不超过1,就是平衡的
套路:因为递归可以经过一个节点三次(第一次;左子树返回(第二次);右子树返回(第三次)),所以我们可以收集到两个子节点的信息再返回到父节点
算法:
如果以每一个节点为头节点的子树都是平衡的,那么整棵树就是平衡的
- 左树是否平衡
- 右树是否平衡
- 左树高度h1,和右树高度h2比较,看是否平衡
- 设计递归返回结构(1. 当前子树的高度 2. 当前子树是否平衡),这两个信息需要返回给父节点(可以构建一个返回类)
public static class ReturnValue{
boolean isBalance;
int height;
public ReturnValue(boolean isBalance, int height) {
this.isBalance = isBalance;
this.height = height;
}
}
用递归列出所有的可能性:
public static ReturnValue process(Node head){
//如果根节点是null,则这个子树是平衡的
if (head == null){
return new ReturnValue(true, 0);
}
ReturnValue leftValue = process(head.left);
ReturnValue rightValue = process(head.right);
//如果左子树不平衡,这棵树就不平衡
if (!leftValue.isBalance){
return new ReturnValue(false,0);
}
//如果右子树不平衡,这棵树就不平衡
if (!rightValue.isBalance){
return new ReturnValue(false,0);
}
//如果左右高度差大于1,这棵树就不平衡
if (Math.abs(rightValue.height-leftValue.height)>1){
return new ReturnValue(false,0);
}
//则目前子树平衡,返回这个子树的相关信息
return new ReturnValue(true, Math.max(rightValue.height, leftValue.height)+1);
}
图解:

2.4 如何判断一棵树是搜索二叉树
右子树比当前节点都大,左子树比当前节点都小,而且通常是没有重复节点的
判断标准:一棵树的中序遍历结果是依次升序的,就是搜索二叉树
2.5 如何判断一棵树是完全二叉树
判断逻辑:
二叉树的按层遍历
- 如果一个Node只有右节点没有左节点,返回false,一定不是完全二叉树
- 如果一个Node只有左节点,或者没有子节点,那么后面遇到的所有节点都必须是叶子节点(层序遍历),否则一定不是完全二叉树
- 以上都可以保证,就是完全二叉树
public static boolean isCBT(Node head){
if (head == null){
return true;
}
Queue<Node> queue = new LinkedList<>();
queue.offer(head);
boolean beginLeaf = false;//是否进入之后的节点都是叶子节点模式?
while(!queue.isEmpty()){
Node cur = queue.poll();
Node left = cur.left;
Node right = cur.right;
//这一条判断语句将两个条件都进行了判断
if (beginLeaf&&(left!=null || right!=null) || left==null&&right!=null){
return false;
}
//层序遍历,将子节点都加进来
if (left!=null){
queue.offer(left);
}
if (right!=null){
queue.offer(right);
}
//如果出现左√右x的情况,开启叶子节点模式
if (left!=null&&right==null){
beginLeaf = true;
}
}
return true;
}
2.5.1 求完全二叉树节点的个数
要求:如果二叉树的节点个数为n,时间复杂度应该低于O(n)
已知情况: 如果满二叉树的层数为 L, 那么这棵二叉树的节点数量为 2^L-1;如果一棵二叉树有n个节点,那么它的层数为log(n)
算法:
- 先遍历head的左边界,可以得到二叉树的层数L
- 遍历head右子树的左边界:
- 如果右子树的左边界到了最后一层,那么这个head节点的左子树是满的:左树的高度就为L-1,可以求得左树的节点数:2(L-1) -1,加上头节点为 2(L-1) 。递归去求右子树的节点个数(其中这个L-1中的1是变化的,表示的是当前head节点所在的层数)
- 如果右子树左边界没有到最后一层,那么右子树一定是满的,只是高度为L-1-1。可以求得右子树的节点个数为2(L-1-1) -1,加上头节点为2(L-1-1) ,递归左子树的节点个数

代码:
//求出以当前节点为头节点的子树的最大深度(绝对深度)
/**
*
* @param head 当前节点
* @param level 当前节点所在的层数
* @return 返回当前节点最深层的左节点的层数(相对于整棵树的层数)
*/
public static int mostLeftLevel(Node node, int level){
while(node!=null){
level++;
node = node.left;
}
return node;
}
/**
*
* @param node 当前被处理的节点
* @param level 当前节点所在的层数
* @param h 整棵树的最大层数
* @return 当前节点为头节点的子树的节点数
*/
public static int process(Node node, int level, int h){
//如果当前节点到达了最大深度,肯定没有子节点了
if(level == h){
return 1;
}
//右子树的深度到达了最大深度,则左子树一定是满二叉树
if(mostLeftLevel(node.right, level+1) == h){
return (1<<(h-level))+process(node.right, level+1, h);
}else{//右子树的深度没有到达最大深度,右子树一定是满二叉树
return (1<<(h-level-1))+peocess(node.left, level+1, h);
}
}
//计算最终的节点数量
public static int nodeCount(Node head){
if(head == null){
return 0;
}
return process(head, 1, mostLeftLevel(head, 1));
}
时间复杂度分析:
- 每一层遍历一个节点(只遍历那个具有满二叉树的节点)一共有n个节点,logn层,复杂度为logn
- 判断深度的时候,只遍历右子树的左边界,依旧是logn
- 所以一共是log2n的复杂度
























 1867
1867

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








