《李宏毅机器学习》- Task1

最新推荐文章于 2025-08-11 19:56:42 发布

Karl_G

最新推荐文章于 2025-08-11 19:56:42 发布

阅读量183

点赞数

CC 4.0 BY-SA版权

分类专栏：机器学习文章标签：李宏毅机器学习正则化梯度下降回归

本文链接：https://blog.youkuaiyun.com/weixin_38424903/article/details/90112345

机器学习专栏收录该内容

3 篇文章

订阅专栏

本文深入探讨了机器学习的基本概念，包括监督学习、非监督学习、半监督学习和强化学习的不同类型，以及中心极限定理、正态分布、最大似然估计等统计学原理的应用。此外，还详细介绍了梯度下降、L1/L2正则化等关键算法，并讨论了模型优化、参数稀疏化的重要性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、了解什么是Machine learning

1、一种映射：

让机器有学习的能力，通过学习，找到可以拟合当前数据类型的最优映射，即

$y = f(x)$ ; 其中x为数据集中的元素，y为对应学习任务的输出结果，F为最优的ML模型

2、两个阶段：Training 和 Testing

1）Training

训练数据x + 模型集(一系列的映射) ——> 最优映射，模型 f

2）Testing

测试数据x + 最优映射，模型 f(Training 的结果) ——> 结果（例如：分类任务则结果为对应测试数据的类别）

3、三个步骤：

1）得到模型集（一系列映射 $f$ ）；

2）衡量映射的好坏 $L(w,b)$ , $f^{_{*}} = argminL(f)$ ；

3）找出最好的映射 $GD$ ；

4、学习任务

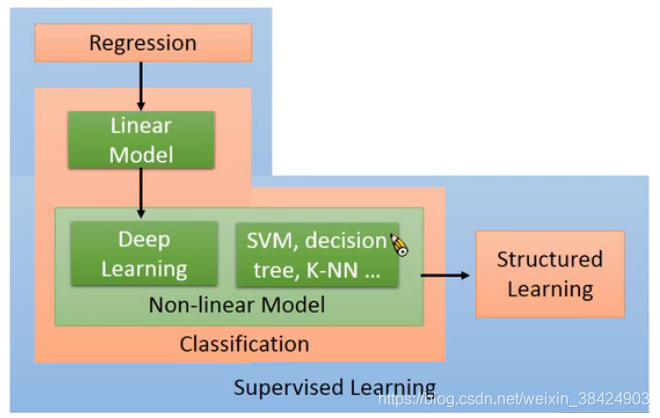
Semi-supervised Learning：部分未标记的数据对已标记数据的训练有一定帮助；未标记类别和已标记类别相同；

Transfer Learning：部分未标记的数据对已标记数据的训练有一定帮助；未标记类别和已标记类别不相同；

Unsupervised Learning：一堆完全未标记的数据或者编码；

Renforcement Learning：对机器学习的结果不再是一个类别，而是该结果的一个得分（该行为的评价），如阿尔法狗；

二、学习中心极限定理，学习正态分布，学习最大似然估计

中心极限定理：对于相互独立的随机变量 $X_{i}$ ，其中 i 代表第i个元素，定理表明，当i足够大时，概率分布近似于正态分布；

最大似然估计：对于给定的概率分布D，假定其连续概率分布和离散概率分布为 $F_{D}$ ，以及一个参数 $\Theta$ ；通过采样，我们可以从这个分布中随机抽取n个样本，并利用n个样本，我们可以计算出其概率 $P(x_{1},x_{2},x_{3},...,x_{n})$ ，而此概率 $P = F_{D}(x_{1},x_{2},...,x_{n}|\Theta )$ ，我们可能不知道 $\Theta$ 的值，但这些数据是服从同一分布的。因此我们可以找到一个 $\Theta$ 是的此时的概率 $P$ 最大，而使得概率（可能性）最大的 $\Theta$ 值即被称为 $\Theta$ 的最大似然估计。