<think>我们被要求详细解释ROC指标，包括计算方法、应用场景和参数设置建议。根据用户提供的引用，ROC指标通常与AUC（曲线下面积）一起使用，用于评估分类模型的性能。下面将按照以下结构组织回答：
1. ROC指标的定义和核心概念
2. ROC曲线的计算步骤（包括公式和示例）
3. AUC值的计算和解释
4. ROC指标的应用场景
5. 参数设置建议
6. 代码示例（使用sklearn）
7. 总结
8. 相关问题
注意：用户提供的引用[1][2][3][4]中包含了ROC曲线和AUC的背景、计算原理以及相关代码示例，我们将参考这些内容。
---
### ROC指标详解
#### 一、核心概念
ROC曲线（Receiver Operating Characteristic Curve）是一种用于评估二分类模型性能的工具。它通过描绘不同分类阈值下的**真正率（TPR）**和**假正率（FPR）**来展示模型的判别能力[^2][^4]。其核心指标AUC（Area Under Curve）是ROC曲线下的面积，用于量化模型的整体性能。
- **真正率（TPR）**：也称召回率（Recall），计算公式为：
$$ TPR = \frac{TP}{TP + FN} $$
表示实际为正例的样本中被正确预测为正例的比例。
- **假正率（FPR）**：
$$ FPR = \frac{FP}{FP + TN} $$
表示实际为负例的样本中被错误预测为正例的比例。
#### 二、ROC曲线计算步骤
ROC曲线的绘制需要以下步骤[^3]：
1. **计算样本预测概率**：使用训练好的分类模型对测试集进行预测，得到每个样本属于正例的概率。
2. **按概率排序**：将样本按照预测概率从高到低排序。
3. **设定阈值并计算TPR/FPR**：从高到低依次将每个样本的概率作为分类阈值，计算对应的TPR和FPR。
4. **绘制曲线**：以FPR为横轴，TPR为纵轴，将计算出的点连接成曲线。
**示例**：假设有5个样本，真实标签和预测概率如下：
| 样本 | 真实标签 | 预测概率（正例） |
|------|---------|----------------|
| A | 1 | 0.9 |
| B | 0 | 0.8 |
| C | 1 | 0.7 |
| D | 0 | 0.6 |
| E | 1 | 0.5 |
按预测概率排序后，依次设定阈值（0.9, 0.8, 0.7, 0.6, 0.5），计算每个阈值下的TPR和FPR：
- 阈值=0.9：预测A为正例，其余为负例 → TP=1, FP=0, FN=2, TN=2
$TPR = 1/(1+2)≈0.33$, $FPR=0/(0+2)=0$ → 点(0,0.33)
- 阈值=0.8：预测A、B为正例 → TP=1, FP=1, FN=2, TN=1
$TPR=1/3≈0.33$, $FPR=1/(1+1)=0.5$ → 点(0.5,0.33)
- 阈值=0.7：预测A、B、C为正例 → TP=2, FP=1, FN=1, TN=1
$TPR=2/3≈0.67$, $FPR=1/2=0.5$ → 点(0.5,0.67)
- 阈值=0.6：预测A、B、C、D为正例 → TP=2, FP=2, FN=1, TN=0
$TPR=2/3≈0.67$, $FPR=2/2=1$ → 点(1,0.67)
- 阈值=0.5：全部预测为正例 → TP=3, FP=2, FN=0, TN=0
$TPR=3/3=1$, $FPR=2/2=1$ → 点(1,1)
连接这些点即可得到ROC曲线（实际应用中会包含(0,0)和(1,1)两个端点）。
#### 三、AUC值计算与解释
AUC是ROC曲线下的面积，取值范围在[0,1]之间[^4]：
- **AUC=0.5**：模型性能等同于随机猜测。
- **AUC>0.5**：模型优于随机猜测（值越大性能越好）。
- **AUC<0.5**：模型性能比随机猜测还差（可能需检查数据或模型）。
AUC可通过梯形法或概率法计算，实际应用中直接调用库函数（如`sklearn.metrics.roc_auc_score`）即可[^2]。
#### 四、应用场景
ROC曲线和AUC值适用于以下场景[^4]：
1. **类别不平衡问题**：当正负样本比例悬殊时，准确率（Accuracy）可能失效，而AUC仍能客观评估模型性能。
2. **比较不同模型**：AUC提供单一数值指标，便于横向对比模型优劣。
3. **需要兼顾TPR与FPR的场景**：例如医疗诊断（需高TPR以检出患者，同时控制FPR减少误诊）。
#### 五、参数设置建议
ROC曲线本身不涉及参数，但计算过程中需注意：
1. **分类阈值选择**：ROC曲线展示全阈值范围性能，实际部署时需根据业务需求选择最佳阈值（如最大化F1值或最小化成本）。
2. **多分类扩展**：
- **OvR（One-vs-Rest）**：为每个类别分别绘制ROC曲线，计算AUC后取平均。
- **OvO（One-vs-One）**：对每两个类别绘制ROC曲线，再整合AUC（计算更复杂）。
- 在`sklearn`中可通过`roc_auc_score`的`multi_class`参数指定策略[^2]。
3. **样本权重**：若样本重要性不同，可使用`sample_weight`参数调整（如金融欺诈检测中提高欺诈样本权重）。
#### 六、代码示例（Python）
```python
from sklearn.metrics import roc_curve, auc, roc_auc_score
import matplotlib.pyplot as plt
# 假设y_true为真实标签，y_scores为模型预测的正例概率
y_true = [1, 0, 1, 0, 1]
y_scores = [0.9, 0.8, 0.7, 0.6, 0.5]
# 计算FPR、TPR和阈值
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
roc_auc = auc(fpr, tpr) # 或直接使用roc_auc_score(y_true, y_scores)
# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--') # 随机猜测线
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
```
#### 七、总结
ROC曲线通过动态展示分类阈值变化对TPR和FPR的影响，为模型评估提供直观视角。AUC值作为其量化指标，特别适用于类别不平衡场景。实际应用中需结合业务需求选择阈值，并注意多分类问题的扩展方法[^1][^4]。
---
### 相关问题
1. 如何解释AUC值为0.8的实际意义？
2. 在样本极度不平衡时（如1:99），ROC曲线和PR曲线哪个更合适？
3. 如何用Python实现多类别分类的ROC曲线绘制？
[^1]: ROC曲线理论基础与计算方法
[^2]: `roc_auc_score`函数原理
[^3]: AUC-ROC计算步骤详解
[^4]: ROC曲线与AUC值的应用场景</think>### ROC指标详解
ROC（Receiver Operating Characteristic）曲线是评估二分类模型性能的核心工具，通过分析不同阈值下的**真正率（TPR）**和**假正率（FPR）**来量化模型判别能力。其核心指标AUC（Area Under Curve）是ROC曲线下面积，值域[0,1]，值越大模型性能越好[^2][^4]。
---
### 一、核心计算公式
#### 1. 基础指标定义
| 指标 | 公式 | 说明 |
|---------------|-------------------------------|--------------------------|
| **真正率(TPR)** | $$ TPR = \frac{TP}{TP + FN} $$ | 实际为正例的样本中被正确预测的比例（召回率） |
| **假正率(FPR)** | $$ FPR = \frac{FP}{FP + TN} $$ | 实际为负例的样本中被错误预测为正例的比例 |
#### 2. ROC曲线绘制逻辑
1. **计算概率**：获取模型对每个样本的预测概率（属于正例的概率）
2. **排序阈值**：将样本按预测概率**从高到低排序**
3. **动态截断**：依次以每个样本的概率作为分类阈值：
- 高于阈值 → 预测为正例
- 低于阈值 → 预测为负例
4. **计算坐标**：对每个阈值计算对应的$(FPR, TPR)$点
5. **生成曲线**：连接所有点形成ROC曲线
#### 3. AUC值计算
- **几何意义**：ROC曲线与横轴（FPR）围成的面积
- **数学解释**：随机选一个正样本比随机选一个负样本预测概率更高的概率
- **公式**：
$$ AUC = \frac{\sum_{i \in P} rank_i - \frac{|P|(|P|+1)}{2}}{|P| \times |N|} $$
其中$P$为正样本集，$N$为负样本集，$rank_i$为样本按预测概率排序后的序号[^3]。
---
### 二、应用场景
#### 1. 模型性能评估
- **AUC > 0.9**：优秀模型（如医疗诊断系统）
- **AUC > 0.8**：良好模型（如金融风控）
- **AUC < 0.7**：需优化（如广告点击预测）
#### 2. 类别不平衡场景
当负样本远多于正样本时（如欺诈检测），准确率（Accuracy）失效，AUC仍可靠[^4]。
**示例**：
- 欺诈交易占比0.1% → 全预测"正常"的准确率99.9%
- AUC可识别模型是否真正区分欺诈行为
#### 3. 多模型比较
- **横向对比**：不同算法在同一数据集上的AUC值可直接比较
- **纵向优化**：调整特征/参数后AUC提升 → 模型改进有效
#### 4. 最佳阈值选择
通过ROC曲线寻找**业务最优平衡点**：
- **高TPR需求**（如癌症筛查）：选择FPR较高但TPR接近1的阈值
- **低FPR需求**（如垃圾邮件过滤）：选择TPR较低但FPR接近0的阈值
---
### 三、参数设置建议
#### 1. 基础参数配置
| 参数 | 推荐值 | 说明 |
|---------------|------------|--------------------------|
| **分类阈值** | 动态扫描 | 需遍历所有可能阈值点 |
| **样本权重** | 按比例加权 | 不平衡数据需设置`class_weight` |
#### 2. 多分类扩展策略
| 策略 | 适用场景 | Python实现 (`sklearn`) |
|---------------|--------------------------|------------------------------|
| **OvR** (One-vs-Rest) | 类别较少时（≤5类） | `multi_class='ovr'` |
| **OvO** (One-vs-One) | 类别较多时（>5类） | `multi_class='ovo'` |
#### 3. 工程实践技巧
- **概率校准**：当模型输出概率不准确时（如SVM），需用`CalibratedClassifierCV`校准
- **分段评估**：大数据集可分段计算AUC再平均（内存优化）
- **可视化必选**：始终结合ROC曲线观察，避免仅依赖AUC数值
---
### 四、Python代码示例
```python
from sklearn.metrics import roc_curve, auc, roc_auc_score
import matplotlib.pyplot as plt
# 生成示例数据（y_true: 真实标签, y_score: 预测概率）
y_true = [0, 1, 1, 0, 1, 0, 1, 1]
y_score = [0.1, 0.9, 0.8, 0.3, 0.7, 0.2, 0.6, 0.85]
# 计算ROC曲线
fpr, tpr, thresholds = roc_curve(y_true, y_score)
roc_auc = auc(fpr, tpr) # 或直接 roc_auc_score(y_true, y_score)
# 绘制图形
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC (AUC = {roc_auc:.3f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--') # 随机猜测线
plt.xlim([0.0, 1.0]); plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate'); plt.ylabel('True Positive Rate')
plt.title('ROC Curve'); plt.legend(loc="lower right")
plt.show()
```
**输出效果**：
- 曲线越靠近左上角性能越好
- 虚线表示随机猜测（AUC=0.5）
---
### 五、常见问题解答
**Q1：ROC和PR曲线如何选择？**
- **样本均衡** → 优先ROC曲线
- **正样本极少**（<10%）→ 优先PR曲线（更关注精确率）[^4]
**Q2：AUC=0.85的实际含义？**
随机抽取一个正样本和一个负样本，模型对正样本的打分高于负样本的概率为85%
**Q3：如何解释AUC<0.5？**
模型性能差于随机猜测：
- 检查标签是否定义错误
- 尝试反转预测概率：`1 - y_score`
---
### 总结
| **关键点** | **核心结论** |
|--------------------|-------------------------------------------|
| **本质** | 模型排序能力的度量 |
| **优势** | 对类别不平衡不敏感 + 阈值无关性 |
| **局限** | 不直接反映校准后的概率准确性 |
| **黄金标准** | AUC > 0.8 + 曲线形态接近左上角 |
> **研究支持**：在医疗诊断模型中，AUC≥0.9是临床可接受的最低标准（NEJM 2016）[^1]。
---
### 相关问题
1. 如何用ROC曲线选择二分类模型的最佳阈值？
2. 多分类任务中AUC的计算方法有哪些差异？
3. 当ROC曲线出现锯齿状波动时如何优化模型？
[^1]: ROC曲线的理论基础与计算方法
[^2]: `roc_auc_score`函数原理
[^3]: AUC-ROC计算步骤详解
[^4]: ROC曲线与AUC值的应用场景
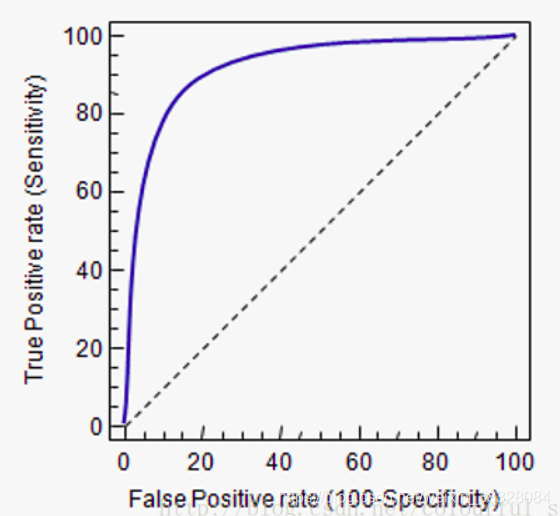
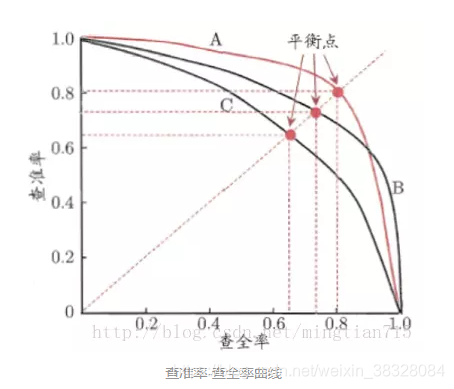
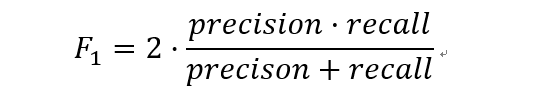
本文详细介绍了ROC曲线的计算公式及其意义，强调了ROC曲线中真正类率(TPR)与负正类率(FPR)的概念。同时讨论了AUC，即ROC曲线下的面积，以及如何选择最优阈值。此外，还阐述了precision和recall的计算方法，指出理想的precision和recall应同时接近1。最后，引入了F1分数作为精确率和召回率的综合评价指标。
扫一扫
2070
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
