BAAI 2020 北京智源大会 | 邢波 | A Blueprint of Standardized and Composable Machine Learning

回放地址

2020 北京智源大会 机器学习专题论坛

报告内容

概述

邢波教授（卡内基梅隆大学机器学习系副主任）的这场talk是一场非常insightful的报告，这场报告的主要点是围绕我们能不能像当年麦克斯韦统一电磁学一样来只用几个方程式就能统一现在众多的ML/AI算法。最后给出了展望：进入这个ML/AI领域的人不必是专家，或者对这方面有丰富知识的人，他们可以从一个最简单的equation开始，然后不断的向上加东西，就像玩乐高一样，然后创造出非常好的，有用的结果。

主要内容

人们对ML/AI的期望越来越高，期待ML/AI能解决人类所有的问题，但是为了实现这些，你会发现有很多困难。你需要处理众多的ML/AI 模型，但是噩梦不在这里，当你选择模型后，你会发现有大量的算法和启发式理论，再此之后，你还需要处理大量不同的数据，如果你运气不好的话，这些数据中可能会包含大量的经验知识需要你来处理。




回顾一下19世纪的物理学，你会发现当时的物理很像我们今天的AI，当时对于电学有大量不同的理论，比如库仑，法拉第，安培；还有光学，万有引力也有很多的理论。

现在的人工智能更像是一个迷宫，现在的人工智能工作，更像是在一个化学实验室，做一些标记，然后创造一些可以教你基准测试的东西。但是当你把这些东西投入到工业界时，你会发现这些经常会变的不可重用，并且非常昂贵。

我们想问我们有没有可能也看到我们人工智能的融合，在那里我们可以对所有的AI都有一个简单的看法。
所以我们进入我们讨论的主题，可以有一个机器学习的蓝图吗？在那里我们可以将不同的方法联系起来，将不同的算法联系起来。并且期待只要几个公式就能处理我们想要解决的任何问题。这就是我们想要建立的问题。
我们设想了一个公式。它由三部分组成：

• Loss
• Optimization solver
• Model architecture

所以这种简单的形式有可能为我们目前所知的machine learning指定一个路线图(draw a roadmap)吗？也许甚至有可能帮助未来的机器学习的研究避免随机的，费劲的实验。

为了便于后面的讲解，引入了一些基本的定义。

回顾了经典方法MLE(有监督和无监督)

即使在早期，这些EM算法也提供了一些很有趣的思想，它打开了通往一类重要算法的大门，称为交替梯度下降（alternative gredient descent），允许您通过交替投影到不同的空间来解决优化问题，为了理解这一点，将log likelihood的形式进行重写，这种形式叫做divergence form，在这种形式下，你可以这样来描述EM算法：在E-step,找到一个分布来让KL-divergence最小。

举了两个例子，Variational EM 和 Wake-Sleep algorithm


做一个小总结，即使仅仅是MLE，你也会发现有大量的算法：EM，VEM，Wake-Sleep，…

将unsupervised MLE和supervised MLE写成divergence minimization的形式。


还有另一种learning framework，叫做Posterior Regularization（PR），这是一个进一步利用divergence minimization的framework。这里的问题变成了在auxiliary distribution $q(x,y)$和需要学习的目标分布$P_{\theta }(x,y)$之间解决KL minimization，同时还有一些约束条件。所以是一个constrained optimization formulation。
使用拉格朗日，可以将它写成unconstrained optimization的形式。由前面的feature function和后面的divergence term两项组成，然后优化发生在两个space中：q和θ。并且MLE可以很容易的写成这种形式。

MLE可以很容易的加入到这个framework中，然后MLE就可以被表达成一个KL 问题。

PR framework不仅能让你引入不同的feature functions，也能让你引入不同的模型设计。

KL divergence是有很多优点的，可以作为loss的一般形式，我想把它称为standard equation 。
将它从原来的约束形式变为看起来更加舒服的形式。
它有三部分组成，1，Experiences，
2，Divergence，Divergence实际上在训练中建立起一个非常有趣的动态过程。一个模型可以是一个老师，不断的教授知识，另一个模型可以是一个学生，迭代的拉近和老师的距离。
3，uncertainty

所以为什么把它称为standard equation呢？我们知道在18,19世纪的物理学上，有很多不同的公式来描述物理现象，有时甚至是相似的现象。但是在麦克斯韦方程组之后，所有的相关的物理公式都可以被描绘成一种标准形式（standard form），因此你不需要将所有的关于电学，光学等的paper都读一遍，你只需要注意这组标准形式就可以了，并且随着现代物理学的发展你可以更进一步的简化它的形式。
虽然这些形式简化了，但是你不会失去描述物理问题的能力。但是它却更容易帮助研究人员，工程师掌握一个知识体系。

现在我们来看一下这个standard equation怎么通过一些很简单的方法来恢复出一些很著名的算法。

我们知道一个非常大的学习框架叫做Active Learning，它有一套全新的方程式和理论，但是在Standard equation下面，Active Learning和其它的Learning并没有太大的区别。

也可以恢复出强化学习(Reinforcement learning)


同时也能恢复出GAN model（介绍了两种方法）


使用standard equation可以恢复出大多数的ML算法。


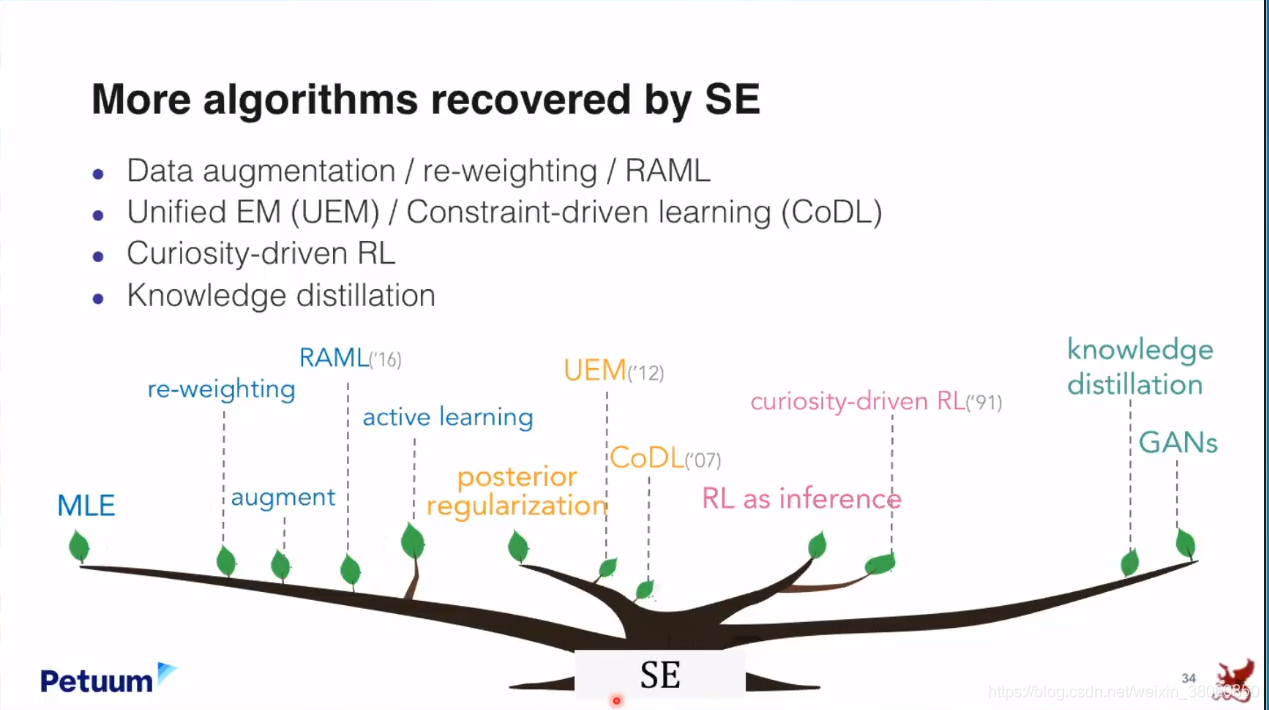
上面讲的是Loss function，我们现在再来看一下Optimization solvers。就像standard equation作为很多算法的master loss形式，是否也有一个master solver来解决optimization的问题呢？
目前还没有一个通用的解决方法，但是Probability functional descent(PFD)也许可能作为一个潜在的通用solver。

PFD实际上一种梯度下降算法，它的操作的关键是通过Gateaux differential推出被称为Influence function的东西，一旦你得到了influence function，那么你就可以得到一个项，并能够使用简单梯度算法进一步优化来得到结果。

但是要向推出influence function可以不会很容易，并且高度依赖于overall loss function的形式。

如果你知道怎么做，那么你就能恢复一些很著名的算法。比如：

• Variational inference for unsupervised MLE
• Policy iteration in RL
• GANs
  
  
  
  这里面也存在一些challenge，比如当你选择稍微不同的loss functions时，就有可能不能够恢复出原来的算法。
  同时，还有许多其它可以选择的算法。
  
  最后再来看一下model architecture
  
  
  

总结部分：有一个ML/AI的蓝图不只是恢复出现在人们已知的公式，如果可能的话，在未来的机器学习研究中，人们会从Standard Equation出发，就像麦克斯韦方程为未来很多研究开启了大门一样。
但在深入那些更难以捉摸的方向前，让我们想想，即使现在，拥有一个ML/AI的蓝图会对我们现在产生什么样的影响？

Reuse and re-purpose of algorithms:




Toward compositionality 还有工具Texar。







最后思考以下这将带我们走向多远。展望：进入这个ML/AI领域的人不必是专家，或者对这方面有丰富知识的人，他们可以从一个最简单的equation开始，然后不断的向上加东西，就像玩乐高一样，然后创造出非常好的，有用的结果。