Heap Sort 的原理及Python实现

最新推荐文章于 2024-10-18 09:40:40 发布

原创

最新推荐文章于 2024-10-18 09:40:40 发布 · 1.7k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#Heap #Sort algorithm

本文介绍了Heap Sort的基本概念，包括其表示方法、如何维护最大堆性质、堆的构建过程以及算法的时间复杂度。重点阐述了如何通过调整操作确保堆的性质，并指出Heap Sort是一种线性时间复杂度的就地排序算法，结合了快速排序和冒泡排序的优势。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.`Heap`表示方法

满足以下性质的二叉树Binary Tree可以成为Binary Heap：

Complete Tree：所有的层都是完全的，除了最后一层，且最后一层的叶子靠左。
Min Heap or Max Heap：根节点是最大值或者最小值，而且这个性质对于任何递归得到的子树都成立。

Binary Heap通常使用array表示：

根节点在array[0];
array[(i-1)//2]返回父节点，array[2*i+1]返回左孩子树，array[2*i+2]返回右孩子树。

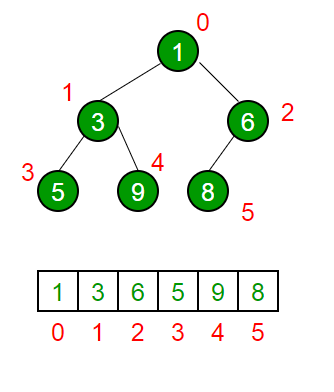
Binary Heap通常使用array表示，对于任意索引i：

def parent(i):
    return (i-1)//2
def left(i):
    return 2*i+1
def right(i):
    return 2*i+2

2.`Max-Heapify`

max heapify是保持max-heap性质的操作，输入为array A and index i，假设输入时，以left(i) and right(i)为根节点的子数都满足最大堆性质，但是以i为根节点的子数不满足最大堆性质。max heapify函数让A[i]向下层转移，进行调整。