排序算法：heap sort（含heap介绍，python）

heap介绍

binary heap可以被看成是一种接近完成的binary tree。可以分为max-heap和min-heap，max-heap的parent要比children大，min-heap相反。
通常用array A构成的heap中，有两个基本的特性：1. A.length，给出了阵列中的元素个数。2. A.heap-size，给出阵列中在heap中的元素。
这两者的区别是，A.heap-size中的才是在heap里的，A.length的长度可能还包含了其他的很多元素。
这个可以在之后的代码中可以看见。比如有一个list有8个元素，但只有前7个元素在heap里，满足heap的特性，则A.length=8, A.heap-size=7。
heap与array的示意图如下。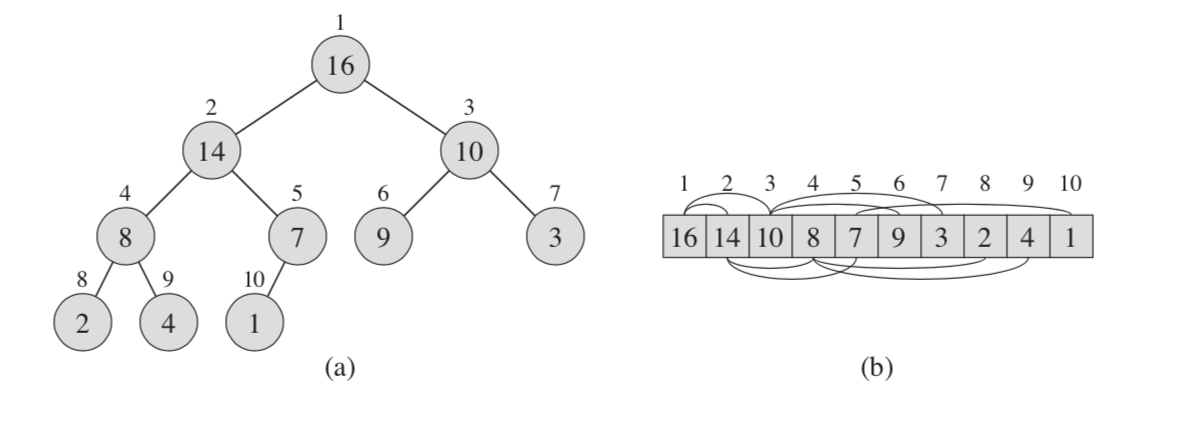

一些特性：

1. 对于每个节点，要想知道其父与子，有以下关系：
   PARENT(i)
   return[i/2]
   LEFT(i)
   return[2i]
   RIGHT(i)
   return(2i+1)
   注意，这里的i是从1开始的，在实际写代码是，一般的list序列都是从0开始，要注意两者之间的不同。这个在之后的代码中会有体现。

2. 要把一个A[1...n]转化成heap，在A([n/2]+1...n)中的所有元素都是heap的叶子。

3. 保持max-heap特性的操作

这个函数结合build Max heap 是保持整个heap特性的关键。下面讨论具体的实现方法

创建一个max heap

首先要实现从某一个节点开始的max heap
算法如下：

此过程的时间复杂度为o(logn）
在此基础上，建立一个max heap的算法如下：

此过程的时间复杂度为o(nlogn）

heap的priority-queue运算

prority-queue是一种数据结构，它的每一个元素都有一个key值，主要有以下几种运算，其使用heap实现的算法如下。
插入一个元素

此过程的时间复杂度为o(logn）
增加一个元素的值

此过程的时间复杂度为o(logn）
提取最大元素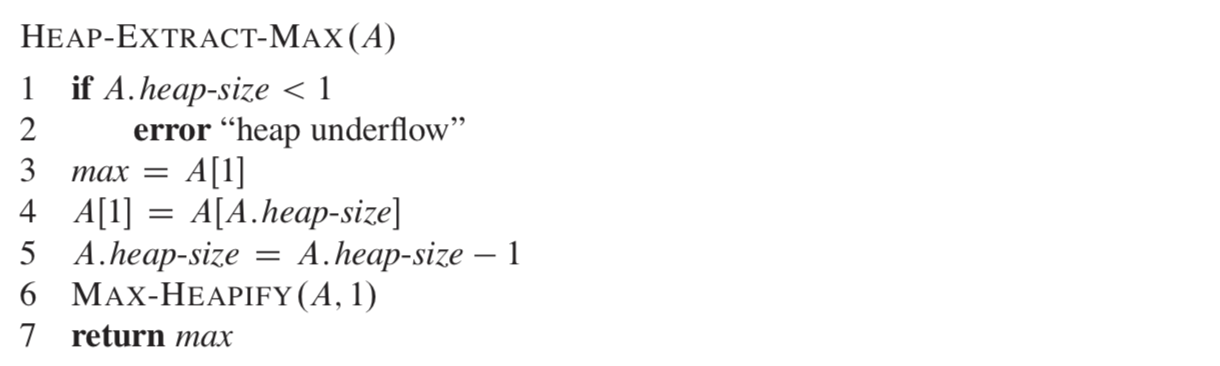

此过程的时间复杂度为o(logn）

从中可以看到heap的一个重要特性，就是它可以将所有priority-queue运算在时间复杂度lgn内完成。

heap的应用：heap sort

整个过程分为

1. 建立heap
2. 提取最大值
3. 放在序列最后
4. 重复指导排序完成
   具体算法如下：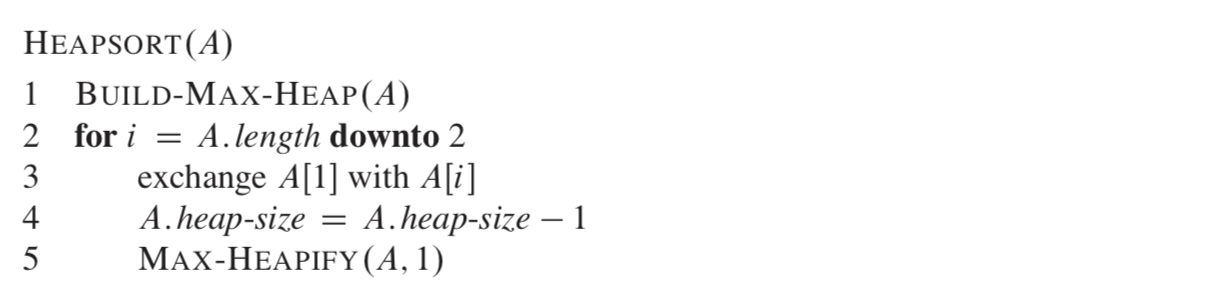
   

实现

#heap
class heap(object):
    def __init__(self,A):
        """
        A is a list
        """
        # self.list = [0]
        self.list = A[:]
        # self.list.insert(0,0)
        self.heapsize = len(A)
        # self.ismaxheap = False
        self.build_max_heap()

    def __str__(self):
        return str(self.list)

    def left(self, i):
        return 2*(i+1)-1
    def right(self, i):
        return 2*(i+1)
    def parent(self, i):
        return (i-1)/2

    def insert(self, key):
        """
        run time o(logn)
        """
        self.heapsize += 1
        self.list.append(-float("inf"))
        self.increase_key(self.heapsize-1,key)

    def increase_key(self,i,key):
        """
        run time o(logn)
        """
        if key < self.list[i]:
            raise ValueError("new key is smaller than current key")
        self.list[i] = key
        while i>0 and self.list[self.parent(i)] < self.list[i]:
            # print("i1="+str(i))
            temp = self.list[i]
            self.list[i] = self.list[self.parent(i)]
            self.list[self.parent(i)] = temp
            i = self.parent(i)
            # print("i2="+str(i))

    def max_heapify(self, i):
        """
        run time: o(logn)
        the key to maintain the max-heap property
        """
        l = self.left(i)
        r = self.right(i)
        # i_m = i
        # largest = 0
        # print("l="+str(l)+" r="+str(r))
        # print(self.heapsize)
        largest = i
        if l < self.heapsize:
            if self.list[l] > self.list[i]:
                largest = l
        # print("r="+str(r)+" largest="+str(largest))
        if r < self.heapsize:
            if self.list[r] > self.list[largest]:
                largest = r
        # print("largest="+str(largest))
        if largest != i:
            temp = self.list[i]
            self.list[i] = self.list[largest]
            self.list[largest] = temp
            self.max_heapify(largest)

    def build_max_heap(self):
        """
        run time: o(nlogn)
        """
        # print(self.heapsize//2)
        for i in range(self.heapsize//2-1,-1,-1):
            # print(i)
            self.max_heapify(i)
        # self.ismaxheap = True

    def extract_max(self):
        """
        build a maxheap and return the max value of it(the first element)
        also pop the first element out of the heap
        run time o(logn)
        """
        if self.heapsize < 1:
            raise ValueError("heap underflow")
        # if self.ismaxheap == False:
            # self.build_max_heap()
        maxele = self.list[0]
        self.list[0] = self.list[self.heapsize-1]
        self.list[self.heapsize-1] = maxele
        self.heapsize -= 1
        self.max_heapify(0)
        return maxele

    def heap_sort(self):
        """
        using recurrence to impelete, can also use for loop
        """
        if self.heapsize == 1:
            return self.list
        self.build_max_heap()
        temp = self.list[0]
        self.list[0] = self.list[self.heapsize-1]
        self.list[self.heapsize-1] = temp
        self.heapsize -= 1
        self.heap_sort()




A = [3,4,5,7,1,4,9]
heap1 = heap(A)
print(heap1)
heap1.insert(2)
print(heap1)
print(heap1.heapsize)
maxele = heap1.extract_max()
print(maxele)
print(heap1)
print(heap1.heapsize)
heap1.increase_key(3,10)
print(heap1)
print(heap1.heapsize)
heap1.heap_sort()
print(heap1)
print(heap1.heapsize)

转载于:https://www.cnblogs.com/litingyu/p/9212413.html