Harris角点检测

1，Harris角点检测基本思想

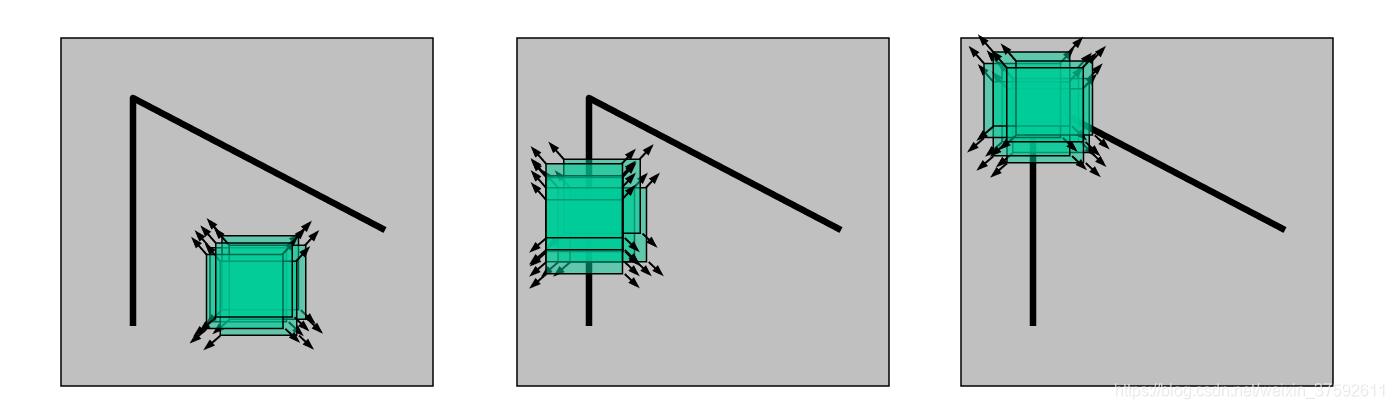
在窗口任意方向移动角点的图像灰度都会发生明显变化；边缘区域只有在左右移动时变化明显，上下移动无变化；平坦区域任意方向移动都无变化。如下图分别为平坦区域，边缘区域和角点时的变化情况

2，Harris检测数学推导 

 设当图像窗口平移[u,v]时产生的灰度变化 为E(U,V)  ，其中W为窗口函数，I(x+u,y+v)为平移后的图像灰度，I(x,y)为原来位置的图像灰度   

     

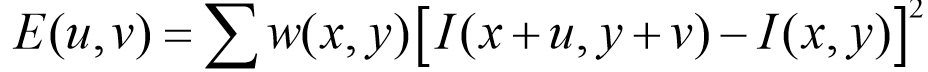
根据二元泰勒展开：

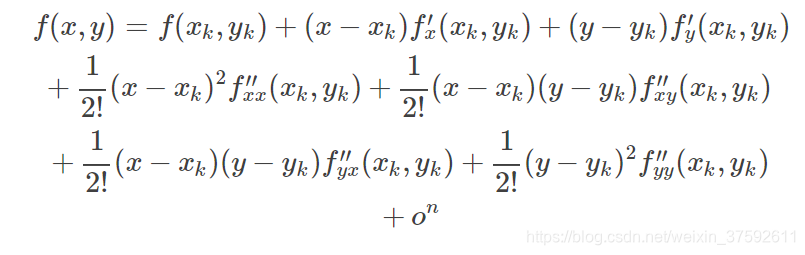
 可知： 

                               

所以

                                                

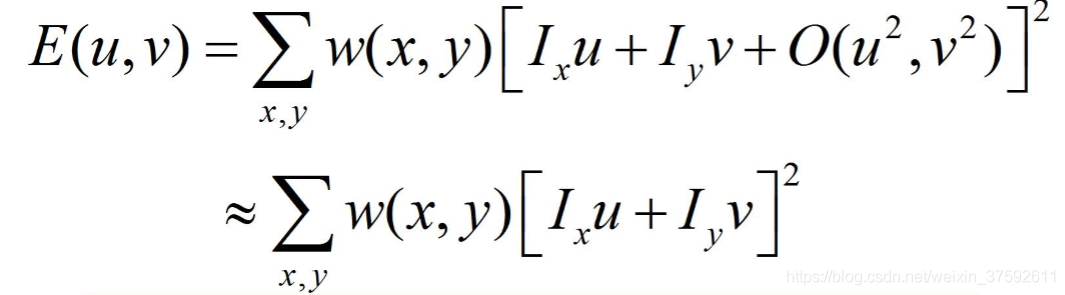
其中

                                           

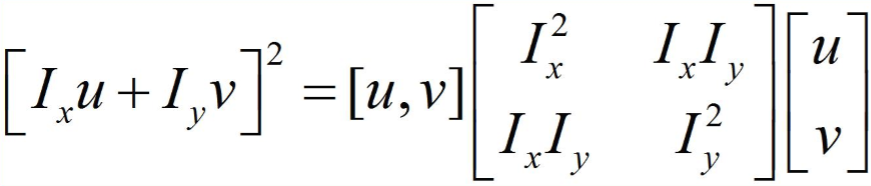
因此当移动量[u,v]取极小值时，

                                            

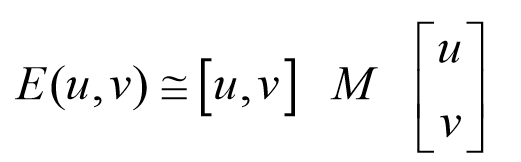
其中M是 2X2 矩阵，可由图像的导数求得：
 

                                        

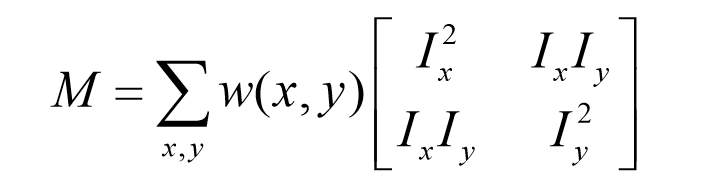
3，矩阵M分析

 Harris角点检测并没有通过直接求E(u,v)的值来判断角点，而是通过对窗口内的每个像素的x方向上的梯度与y方向上的梯度进行统计分析。虽然我们利用E(u,v)来描述角点的基本思想，然而最终我们仅仅使用的是矩阵M，通过获取矩阵的两个特征值对图像进行分类 ：   

                                    

 

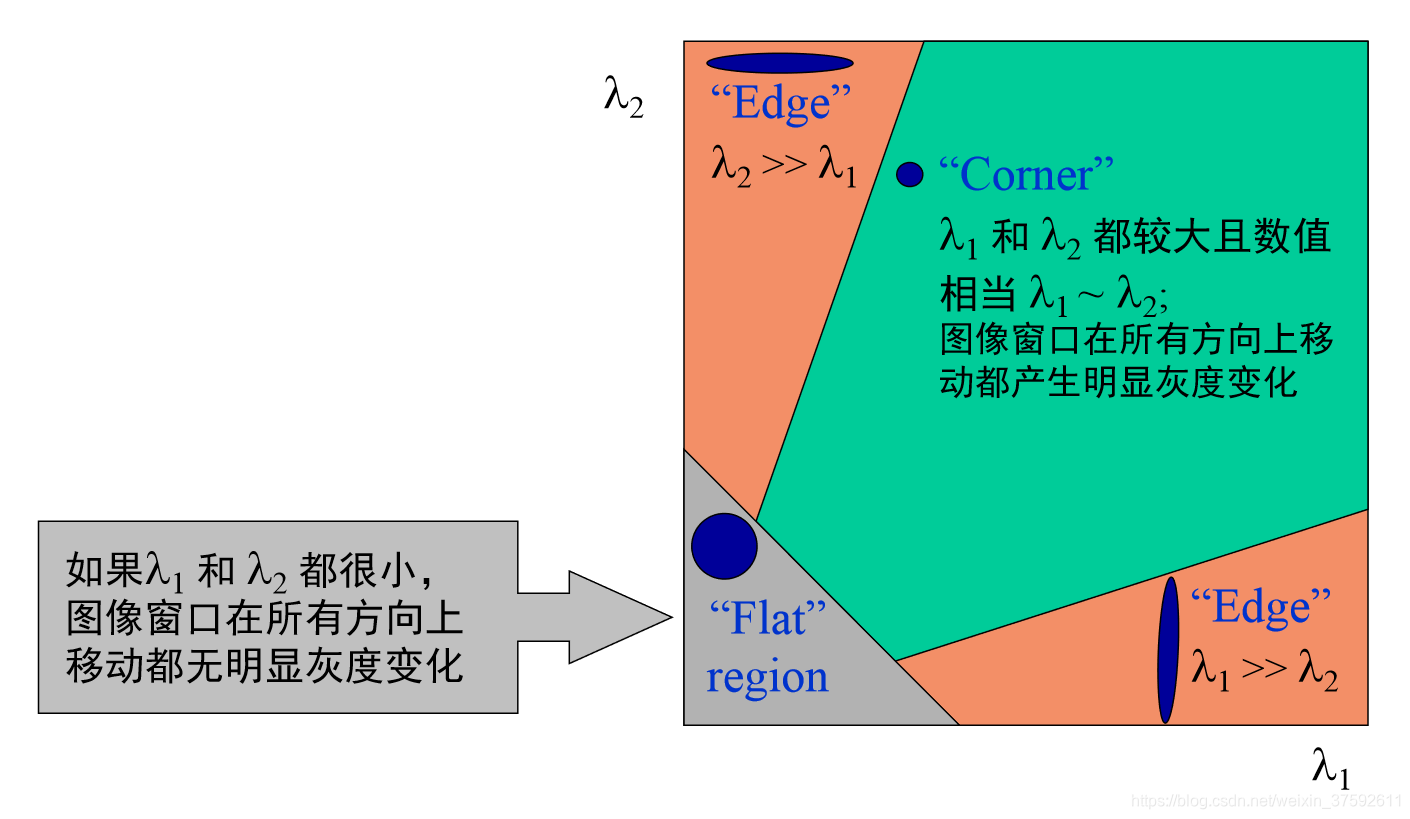
4，角点响应函数

                                                                       

 

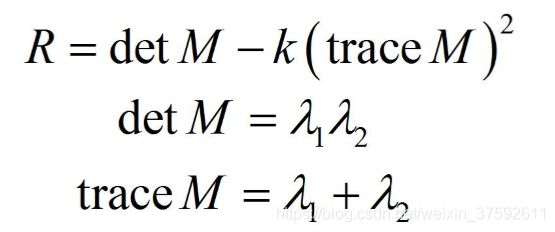
其中，R 只与M的特征值有关 

角点：R 为大数值正数 •=

 边缘：R为大数值负数 

 平坦区：R为小数值
所以可以用R判断是否是角点

5，python实现

harris.py

from scipy.ndimage import filters
from numpy import *
from pylab import *


def compute_harris_response(im, sigma=3):
    imx = zeros(im.shape)  # 计算导数
    filters.gaussian_filter(im, (sigma, sigma), (0, 1), imx)
    imy = zeros(im.shape)
    filters.gaussian_filter(im, (sigma, sigma), (1, 0), imy)
    Wxx = filters.gaussian_filter(imx * imx, sigma)
    # 计算harris矩阵分量
    Wxy = filters.gaussian_filter(imx * imy, sigma)
    Wyy = filters.gaussian_filter(imy * imy, sigma)
    Wdet = Wxx * Wyy - Wxy ** 2  # 计算矩阵的特征值和迹
    Wtr = Wxx + Wyy
    return Wdet / Wtr


def get_harris_points(harrisim, min_dist=10, threshold=0.1):
    conner_threshold = harrisim.max() * threshold
    harrisim_t = (harrisim > conner_threshold) * 1

    coords = array(harrisim_t.nonzero()).T
    candidate_values = [harrisim[c[0], c[1]] for c in coords]
    index = argsort(candidate_values)
    allowed_locations = zeros(harrisim.shape)
    allowed_locations[min_dist:-min_dist, min_dist:-min_dist] = 1
    filtered_coords = []
    for i in index:
        if allowed_locations[coords[i, 0], coords[i, 1]] == 1:
            filtered_coords.append(coords[i])
            allowed_locations[(coords[i, 0] - min_dist):(coords[i, 0] + min_dist),
            (coords[i, 1] - min_dist):(coords[i, 1] + min_dist)] = 0  # 此处保证min_dist*min_dist只有一个harris特征点
    return filtered_coords


def plot_harris_points(image, filtered_coords):
    figure()
    gray()
    imshow(image)
    plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '+')
    axis('off')
    show()

testHarris.py

from PIL import Image

from numpy import *
import harris
from pylab import *
from scipy.ndimage import filters

im = array(Image.open('empire.jpg').convert('L'))
harrisim = harris.compute_harris_response(im)
filtered_coords = harris.get_harris_points(harrisim)
harris.plot_harris_points(im, filtered_coords)

实验结果

                                                             

参考文章： 

https://blog.youkuaiyun.com/zhouyelihua/article/details/40087045