本文详细介绍了Harris角点检测算法与SIFT（尺度不变特征变换）的原理、步骤及应用场景。通过实验展示了在不同场景下，Harris角点检测器和SIFT特征匹配的性能，分析了两者的优缺点。实验结果显示，SIFT在特征匹配和旋转不变性方面表现出色，但对尺度变化敏感；Harris角点检测则在运行效率和角度不变性上具有一定优势，但对尺度和光照变化的鲁棒性较弱。
目录
前言
本次实验通过参考教材《Python计算机视觉编程》和网上大量资料学习局部图像描述子，Harris角点检测器，SIFT特征，匹配地理标记图像相关内容。
一、Harris角点检测算法
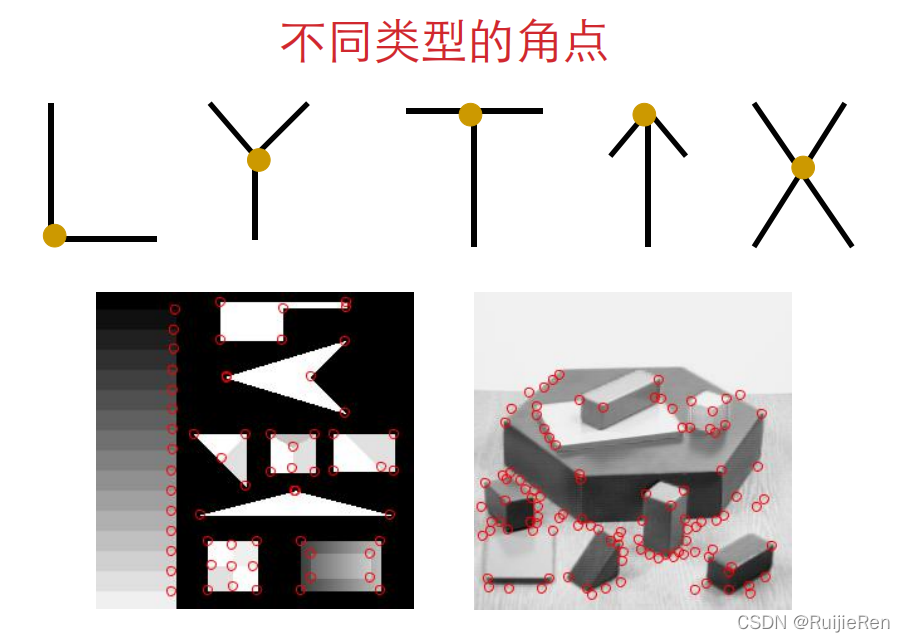
1.1 角点是什么
角点具有的特征：
<1>轮廓之间的交点；
<2>局部窗口沿任意方向移动，均产生明显变化的点；
<3>图像局部曲率突变的点；
<4>对于同一场景，即使视角发生变化，通常具备稳定性质的特征；
<5>该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化。
1.2 好的角点检测算法具备的特征
<1>检测出图像中“真实的”角点；
<2>准确的定位性能；
<3>具有很高的稳定性；
<4>具有对噪声的鲁棒性；
<5>具有较高的计算效率。
1.3 角点检测算法基本原理
基本原理：
人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，如果滑动前后窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了角点；如果滑动前后窗口内区域的灰度没有发生变化那么窗口内就不存在角点。
1.4 用数学方法刻画角点特征
首先，将图像窗口平移[u,v]产生灰度变化的自相关函数如下：
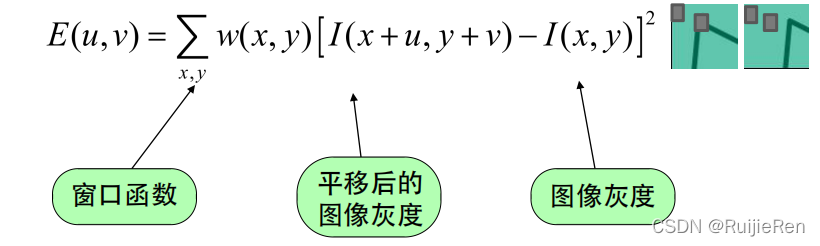
其中窗口函数（权重矩阵）可以是平坦的，也可以是高斯的如下图（权重矩阵W（通常为高斯滤波器Gσ）：
然后将I(x+u，y+v)函数在（x,y）处泰勒展开得：
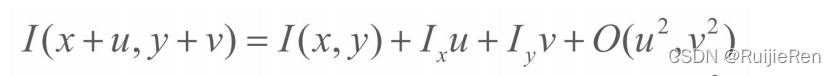
则：
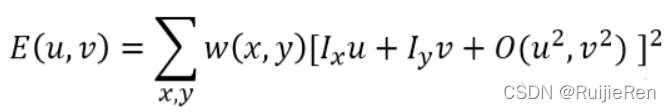
其中Ο(u2,v2)近似为0， 由于是对局部微小的移动量 [u,v]，所以可以近似得到下面忽略余项之后的表达式为一个二项式函数：
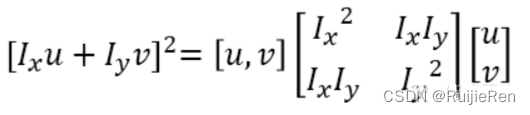
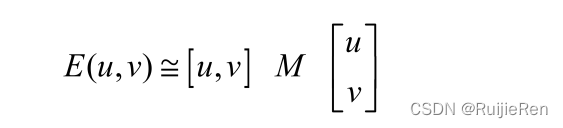
其中M是2X2矩阵，可由图像得导数求得：
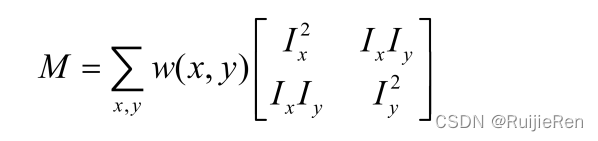
忽略余项之后的表达式为一个二项式函数，然而二项式函数的本质上就是一个椭圆函数，椭圆的扁率和尺寸是由M(x,y)的特征值λ1、λ2决定的，
椭圆的方向是由M(x,y)的特征矢量决定的，如下图所示，椭圆方程为：
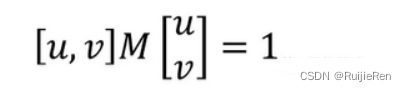
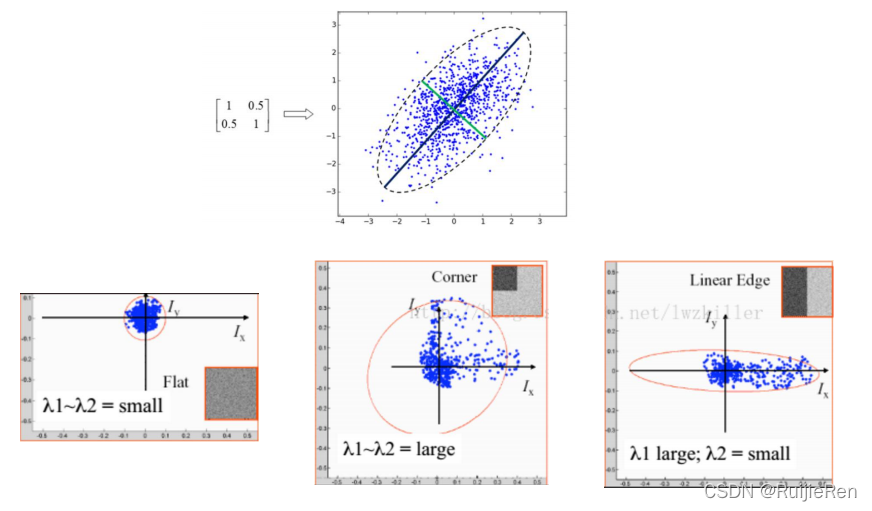
椭圆函数特征值与图像中的角点、直线（边缘）和平面之间的关系如下图所示。共可分为三种情况：
（1） 图像中的直线：一个特征值大，另一个特征值小，λ1>λ2或λ2>λ1。自相关函数值在某一方向上大，在其他方向上小。
（2）图像中的平面：两个特征值都小，且近似相等；自相关函数数值在各个方向上都小。
（3）图像中的角点：两个特征值都大，且近似相等，自相关函数在所有方向都增大。
通过M的两个特征值λ1和λ2的大小对图像点进行分类：
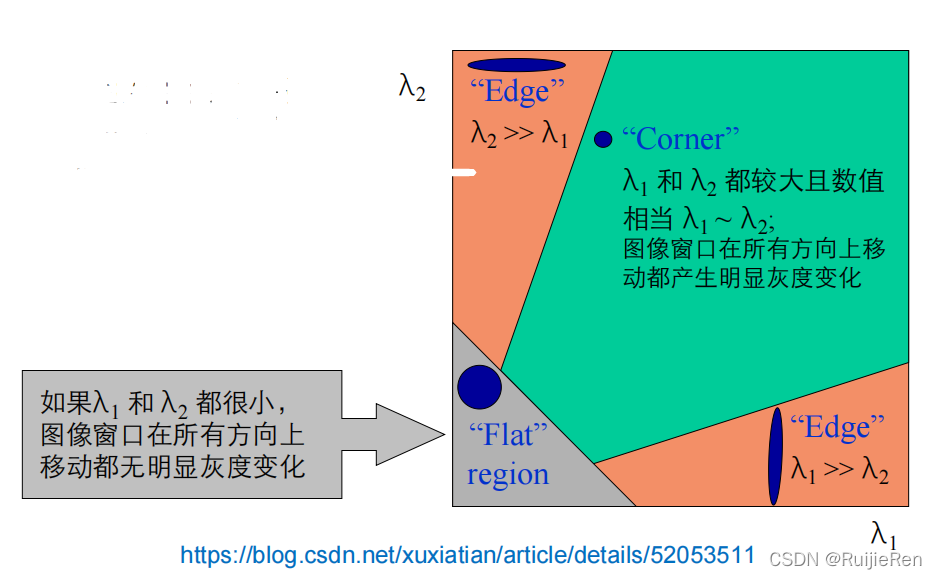
1.5 定义角点响应函数
由于我们是通过M的两个特征值的大小对图像进行分类，所以，定义角点相应函数R：
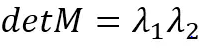
其中k为经验常数，一般取k=0.04~0.06。增大k的值将减小响应值R，降低检测的灵敏性，减少被检测角点的数量；减小k值，将增大角点响应值R，增加被检测角点的数量。为了去除加权常数κ，我们通常使用商数detM/(traceM)2作为指示器。所以，上图可以转化为：
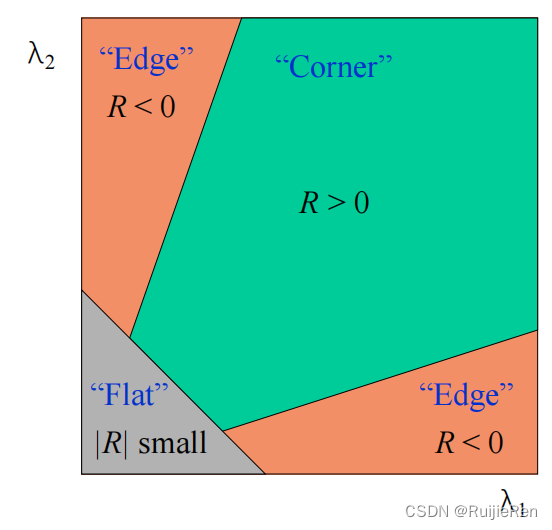
其中：
• R 只与M的特征值有关
• 角点：R 为大数值正数（λ1和λ2都是很大的正数）
• 边缘：R 为大数值负数
• 平坦区：R 为小数值（如果λ1≈λ2≈0，该区域为空）
在判断角点的时候，对角点响应函数R进行阈值处理：R > threshold，提取R的局部极大值。
1.6 Harris角点检测步骤
Harris角点检测可以分为5个步骤：
（1）计算图像I(x,y)I(x,y)在xx和yy两个方向的梯度IxIx,IyIy;
（2）计算图像两个方向梯度的乘积;
（3）使用高斯函数对Ix2、Iy2、IxIy进行高斯加权(取σ=2,ksize=3)，计算中心点为(x,y)(x,y)的窗口W对应的矩阵M；
（4）计算每个像素点(x,y)处的(x,y)处的Harris响应值R；
（5）过滤大于某一阈值t的R值；
1.7 Harris角点检测算法的响应函数
Harris角点检测器的响应函数会返回像素值为 Harris 响应函数值的一幅图像。
代码展示：
# 角点响应函数
import numpy as np
from scipy.ndimage import filters
# 返回像素值为Harris响应函数值得一幅图像
def compute_harris_response(im, sigma=3):
""" 在一幅灰度图像中，对每个像素计算Harris角点检测器响应函数 """
# 计算导数
imx = np.zeros(im.shape)
filters.gaussian_filter(im,(sigma,sigma),(0,1),imx)
imy = np.zeros(im.shape)
filters.gaussian_filter(im,(sigma,sigma),(1,0),imy)
# 计算Harris矩阵的分量
Wxx = filters.gaussian_filter(imx*imx,sigma)
Wxy = filters.gaussian_filter(imx*imy,sigma)
Wyy = filters.gaussian_filter(imy*imy,sigma)
# 计算特征值和迹
Wdet = Wxx * Wyy - Wxy**2
Wtr = Wxx + Wyy
return Wdet / Wtr得到像素值为Harris响应函数值的图像后，我们需要从这幅图像中挑选出需要的信息，然后选取像素值高于阈值的所有图像点；再加上额外的限制，即角点之间的间隔必须大于设定的最小距离。这种方式会产生很好的角点检测结果。为了实现该算法，我们获取所有的候选像素点，以角点响应值递减的顺序排序，然后将距离已标记为角点位置过近的区域从候选像素点中删除。代码如下：
def get_harris_points(harrisim, min_dist=10, threshold=0.1):
"""从一幅Harris响应图像中返回角点。min_dist为分割角点和图像边界的最少像素数目"""
# 寻找高于阈值的候选角点
corner_threshold = harrisim.max() * threshold
harrisim_t = (harrisim > corner_threshold) * 1
# 得到候选角点的坐标
coords = np.array(harrisim_t.nonzero()).T
# 以及他们的Harris响应值
candidate_values = [harrisim[c[0], c[1]] for c in coords]
# 对候选点按照Harris响应值进行排序
index = np.argsort(candidate_values)
# 将可行点的位置保存到数组中
allowed_locations = np.zeros(harrisim.shape)
allowed_locations[min_dist:-min_dist, min_dist:-min_dist] = 1
# 按照min_distance原则，选择最佳Harris角点
filtered_coords = []
for i in index:
if allowed_locations[coords[i:0], coords[i, 1]] == 1:
filtered_coords.append(coords[i])
allowed_locations[(coords[i, 0] - min_dist):(coords[i, 0] + min_dist),
(coords[i, 1] - min_dist):(coords[i, 1] + min_dist)] = 0
return filtered_coords
1.8 Harris角点检测实例
测试不同阈值下的检测结果，代码如下：
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from Localdescriptors import harris
# 读入图像
img = np.array(Image.open('../image/JMU_5.jpg').convert('L'))
# 检测Harris角点
harrisim = harris.compute_harris_response(img)
# Harris响应函数
harrisim1 = 255 - harrisim
# print(harrisim1)
# 使其标题可以显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure()
plt.gray()
plt.subplot(141)
plt.imshow(harrisim1)
plt.title('harris响应函数值图像')
plt.axis('off')
filtered_coords1 = harris.get_harris_points(harrisim, 6, 0.01)
filtered_coords2 = harris.get_harris_points(harrisim, 6, 0.05)
filtered_coords3 = harris.get_harris_points(harrisim, 6, 0.1)
plt.subplot(142)
harris.plot_harris_points(img,filtered_coords1)
plt.title('阈值为0.01')
plt.subplot(143)
harris.plot_harris_points(img, filtered_coords2)
plt.title('阈值为0.05')
plt.subplot(144)
harris.plot_harris_p
最低0.47元/天 解锁文章
扫一扫
191
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
