UVALive7670 Asa's Chess Problem,上下界费用流,另类解法

Asa’s Chess Problem

先阐述一下带上下界的边怎么建.

---

带上下界的建图方法

设我要建一条边$(u\to v)$,流量上界为$up$,下界为$down$,费用为$cost$.则我需要建两条边.

为保证一定会有$down$的流量流过去,我们可以建立一条$u\to v$的边,容量为$down$,费用为$-inf+cost$,这样保证了一旦有解,一定会有$down$的流量流过来.

随后,再建立一条从$u\to v$的边,容量为$up-down$,费用为$cost$的边.这样保证了还会再流至多$up-down$的流量,但不是强制要流.

判断解是否有解

算出所有边的$down$之和$sd$,算出最后的费用包含$si$个$-inf$.如果$si==sd$则说明有解,否则无解.

计算实际的费用

实际的费用就是$(inf-((-tot\_cost)\%inf))$.
上面的式子就是实际的答案.

---

正文

简单情形

先考虑我们拿到的矩阵之间的元素是不可交换的,要求检查该矩阵满足条件的可行性.

那么这是一个经典问题,建图方法如下:

源点$S(0)$向行$R(1-n)$连接一条流量为该行上下界且费用为$0$的边.

列$C(n+1-2n)$向汇点$T(2n+1)$连接一条流量为该列上下界且费用为$0$的边.

每个点$P(x,y)$表示从$R(x)$向$C(y)$连接一条容量为点的权值,费用为$0$的边.最后看一下是否满流且下界边流满即可.

复杂情形

那么回到这个题,相当于增加了格点之间可交换这个条件(注意可交换的格点对之间至少有一个坐标是相同的,这是题目给出的条件之一).

如果两个格点相同,那么完全没有交换的必要(直接按照简单情形连边即可),因此我们只考虑两个格点不同的情况.

设$P(x_1,y_1)$为黑色(1),$P(x_2,y_2)$为白色(0).考虑它们之间连边方案.

1. 当$y_1=y_2$时,无论交换与否,最后流量都是流向$y_1$这列.但是交换与否影响流量是从$x_1$行流入还是$x_2$行流入.
   
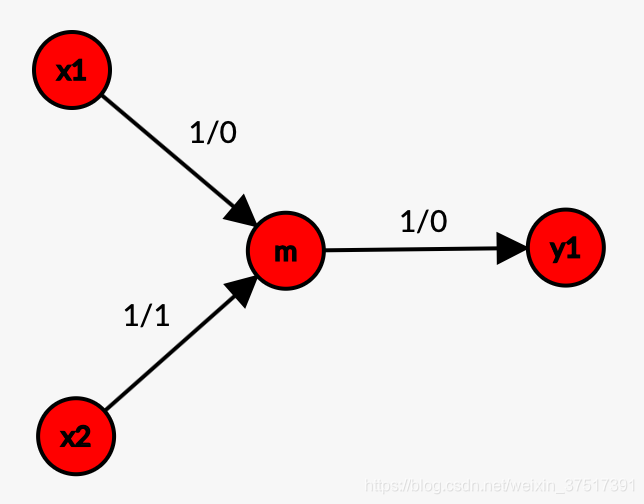
2. 当$x_1=x_2$时,无论交换与否,最后流量都是从$x_1$这行流出.但是交换与否影响流量是从$y_1$行流出还是$y_2$行流出.
   

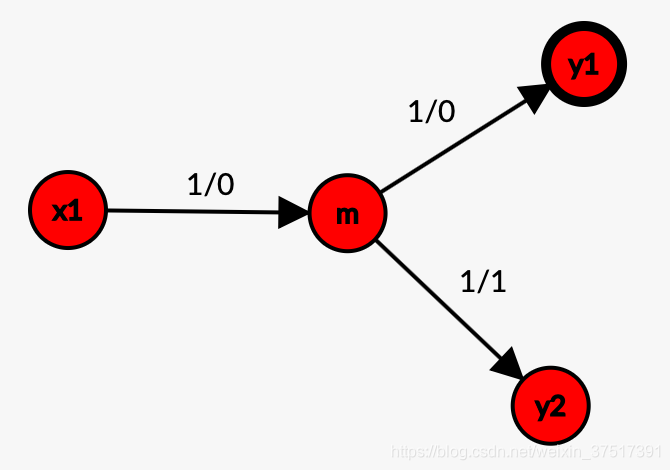
实现代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define pr(x) std::cout << #x << ':' << x << std::endl
#define rep(i,a,b) for(int i = a;i <= b;++i)
using namespace std;
#define int long long
const int inf = 1e10;
const int mm = 111111;
const int maxn = 3000;
int node,src,dest,edge;
int ver[mm],flow[mm],cst[mm],nxt[mm];
int head[maxn],work[maxn],dis[maxn],q[maxn];
int tot_cost;
void prepare(int _node,int _src,int _dest)
{
    node=_node,src=_src,dest=_dest;
    for(int i=0; i<node; ++i)head[i]=-1;
    edge=0;
    tot_cost = 0;
}
void add_edge(int u,int v,int c,int cost)
{
    ver[edge]=v,flow[edge]=c,nxt[edge]=head[u],cst[edge]=cost,head[u]=edge++;
    ver[edge]=u,flow[edge]=0,nxt[edge]=head[v],cst[edge]=-cost,head[v]=edge++;
}
int ins[maxn];
int pre[maxn];
bool Dinic_spfa()
{
    memset(ins,0,sizeof(ins));
    //memset(dis,inf,sizeof(dis));
	rep(i,0,maxn-1) dis[i] = 10000*inf;
    memset(pre,-1,sizeof(pre));
    queue<int> Q;
    //int i,u,v,l,r=0;
    Q.push(src);
    dis[src] = 0,ins[src] = 1;
    pre[src] = -1;
    while(!Q.empty()){
        int u = Q.front();Q.pop();
        ins[u] = 0;
        for(int e = head[u];e != -1;e = nxt[e]){
            int v = ver[e];
            if(!flow[e]) continue;
            if(dis[v] > dis[u] + cst[e]){
                dis[v] = dis[u] + cst[e];
                pre[v] = e;
                if(!ins[v]) ins[v] = 1,Q.push(v);
            }
        }    	
    }
    return dis[dest] < 10000*inf;
}
int Dinic_flow()
{
    int i,ret=0,delta=inf;
    while(Dinic_spfa())
    {
        for(int i=pre[dest];i != -1;i = pre[ver[i^1]])
    		delta = min(delta,flow[i]);
		for(int i=pre[dest];i != -1;i = pre[ver[i^1]])
    		flow[i] -= delta,flow[i^1] += delta;
		ret+=delta;
		tot_cost += dis[dest]*delta;
    }
    return ret;
}
int n;
int a[55][55];
signed main() {
	std::ios::sync_with_stdio(false);
	while(std::cin >> n && n) {
		int suml = 0,who = 0;
		prepare(2+2*n+n*n/2,0,2*n+1);
		rep(i,1,n) rep(j,1,n) {
			std::cin >> a[i][j];
			who += a[i][j];
		}
		rep(i,1,n) {
			int l,h;
			std::cin >> l >> h;
			suml += l;
			if(l > 0) 
				add_edge(0,i,l,-inf);
			if(h-l > 0)
				add_edge(0,i,h-l,0);
		}

		rep(i,1,n) {
			int l,h;
			std::cin >> l >> h;
			suml += l;
			if(l > 0) 
				add_edge(n+i,2*n+1,l,-inf);
			if(h-l > 0)
				add_edge(n+i,2*n+1,h-l,0);
		}

		int tot = 2*n+1;
		rep(i,1,n*n/2) {
			int x1,x2,y1,y2;
			std::cin >> x1 >> y1 >> x2 >> y2;
			if(a[x1][y1] + a[x2][y2] == 2) {
				add_edge(x1,n+y1,1,0);
				add_edge(x2,n+y2,1,0);
			}
			else if(a[x1][y1] + a[x2][y2] == 1) {
				++tot;
				if(y1 == y2) {
					add_edge(x1,tot,1,!a[x1][y1]);
					add_edge(x2,tot,1,!a[x2][y2]);
					add_edge(tot,n+y1,1,0);
				}
				else if(x1 == x2){
					add_edge(x1,tot,1,0);
					add_edge(tot,n+y1,1,!a[x1][y1]);
					add_edge(tot,n+y2,1,!a[x2][y2]);
				}
			}
		}
		
		int myflow = Dinic_flow();
		tot_cost *= -1;
		int pass = (tot_cost+inf-1)/inf;
		if(pass != suml || myflow != who) {
			std::cout << -1 << std::endl;
			continue;
		}
		std::cout << (inf - (tot_cost % inf))%inf << std::endl;
	}	
	return 0;
}