IT TAKES TWO: YOUR GRPO IS SECRETLY DPO
观点:GRPO本质上是一种对比学习算法,与Direct Preference Optimization(DPO)密切相关。
基于这一洞察,作者提出了2-GRPO——仅使用两个响应分组的GRPO变体。
理论上,2-GRPO保持了无偏梯度估计;
实验上,它在多个数学推理任务中与16-GRPO性能相当,同时将训练时间减少70%以上, rollout数量减少至1/8。
这项研究不仅揭示了GRPO的内在机制,还为资源受限的LLM后训练提供了高效解决方案。
研究动机:为什么重新思考GRPO?
GRPO传统观点认为,大分组大小(如G=16)能提供更稳定的奖励归一化,避免梯度估计偏差。然而,生成大量响应是计算瓶颈——在典型设置中,rollout生成占训练时间的70%。
论文从一个新视角切入:
GRPO的组内归一化本质上是在执行对比学习。
具体来说,优势值为正的响应被视为“正样本”,优势值为负的视为“负样本”,目标是通过梯度更新提高正样本概率、降低负样本概率。
这一视角自然地将GRPO与DPO联系起来——DPO是RLHF中常用的算法,仅使用一对正负响应进行优化。
如果DPO能用一对样本成功,GRPO为什么不能?这一疑问促使作者探索最小分组大小G=2的可行性,即2-GRPO。
对比学习框架
论文定义了一个通用对比损失函数:
通过证明GRPO和DPO的梯度均符合此形式,
论文得出结论:两者都是对比学习算法。
GRPO通过组内归一化隐式定义正负样本,而DPO直接使用标注数据。
对比学习的梯度
GRPO的真实目标
他的梯度
核心理论分析:为什么2就足够?
优势估计的无偏性
论文通过命题4.1证明,在二值奖励设置中,2-GRPO的优势估计与标准GRPO仅差一个缩放因子:
标准GRPO:
2-GRPO:
这意味着2-GRPO的优势估计是无偏的,且与策略正确概率§相关,足以引导优化方向。
梯度方差可控
减少分组大小会增加每个样本的梯度方差,但论文指出,通过增加提示数量(batch size)可以补偿。
具体地,如果总rollout数固定(如B=Q×G),减少G时增加Q可以保持总体方差可控。
实验中,2-GRPO使用batch size=256(vs. 16-GRPO的32),有效平衡了方差。
困难问题上的探索能力
有人担心小分组在困难问题上采样不到正样本,但命题4.4证明:在相同总rollout数下,2-GRPO的探索能力不弱于大分组。
因为模型在训练中逐步改进,后期策略的正确概率更高,更容易采样到正样本。
实验验证:2-GRPO是否真的有效?
实验设置
模型:Qwen-1.5B、Qwen-7B、DeepSeek-1.5B
数据集:MATH、DAPO-Math-Sub(训练集);MATH-500、AMC23等(测试集)
评估指标:Mean@32(平均准确率)、Pass@32(至少一次正确的概率)
对比方法:16-GRPO vs. 2-GRPO
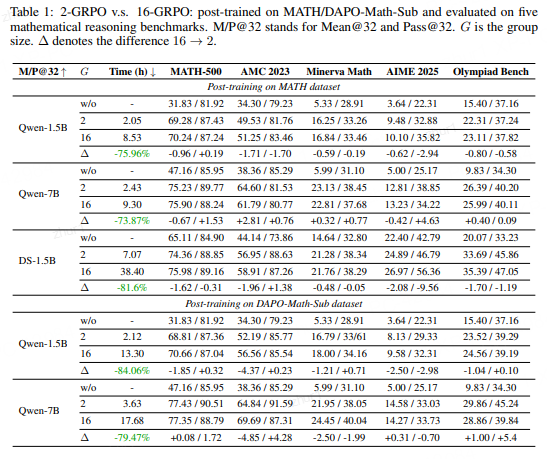
上表展示了在五个数学推理基准上的结果。关键发现:
- 性能相当:2-GRPO在大多数任务上与16-GRPO相差无几,甚至部分任务略优。
- 效率大幅提升:训练时间减少70%-84%,rollout数量减少87.5%。
- 模型通用性:在不同规模模型(1.5B、7B)和数据集上均一致有效。
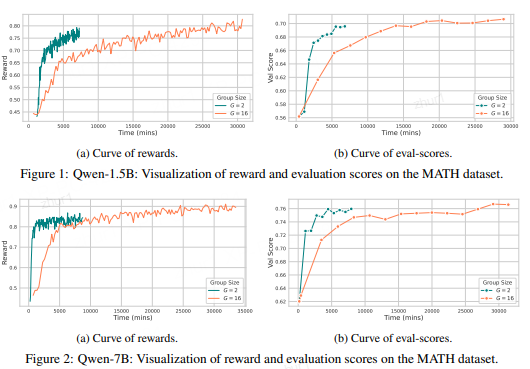
可视化分析
Qwen-7B在MATH数据集上的奖励和评估分数趋势
可见2-GRPO与16-GRPO曲线高度重合,说明其在分布内泛化能力相当。
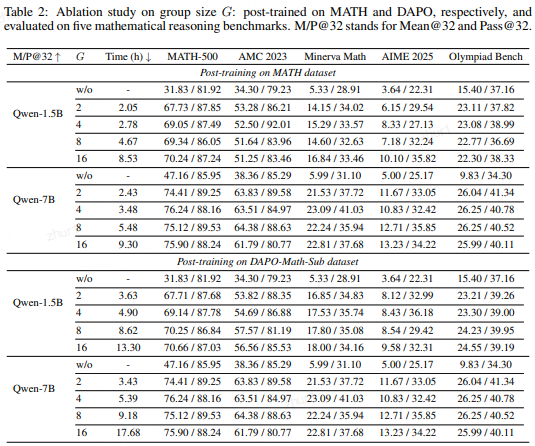
消融实验
表展示了不同分组大小(G=2,4,8,16)的消融结果。随着G减小,性能略有波动,但2-GRPO仍保持竞争力,且训练时间显著降低。
讨论与局限性
论文指出2-GRPO的进一步优化方向:
- 零优势rollout的梯度计算:当前即使优势为0,仍需前向计算,未来可优化。
- 数据效率:2-GRPO会丢弃许多rollout(当策略极好或极差时),可能限制模型达到最优。未来可探索自适应分组大小。
- 理论扩展:当前分析基于二值奖励,未来可扩展到连续奖励场景。
 2-GRPO:对比学习的高效方案
2-GRPO:对比学习的高效方案





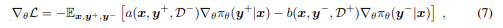
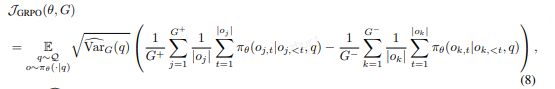

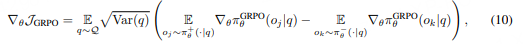

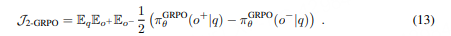
















 2040
2040

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








