《Fast Inference from Transformers via Speculative Decoding》:
1. 基本概念
(1) Two Models
Mp:target model,即原始模型。
Mq:efficient approximation model,即近似模型。
Mq比Mp小(参数量),暂且称Mq为小模型,Mp为大模型。
(2) Two distributions
这里p(x)、q(x)分别是Mp、Mq在给定输入x<t下生成下一个token的概率分布。
(3) Process
- 简单一轮:生成->评估(接受,拒绝)->重新采样
- 完整一轮:先用小模型Mq生成 r 个token(auto regression自回归方式);然后用大模型Mp来评估(并行解码 r 次,生成 r +1个token),依次对Mq生成的每一个token,比较两个模型的概率分布,来决定是接受还是拒绝;
若拒绝,那么对拒绝token所在的位置的分布做一个调整,然后重新采样生成一个新token之后就结束。
若全都接受,那么这一轮一共r+1生成了个token,其中前r个由生成,第r+1个由Mp生成。
显然,经过一轮speculative decoding,最多可生成 r+1 个token,最少生成1个token。
(4)为啥叫speculative decoding
对于为啥叫speculative decoding或者为啥大家喜欢叫投机解码?
利用小模型Mq生成的 r 个token是推测的(可能的)结果,并不是真正最后输出的结果,这些结果需要通过模型Mp去决定对不对,要不要。
显然,speculative decoding的核心思想就是“先猜测,后验证”。但是这种猜测行为实际上是比较“冒险的”,因为有可能被拒绝。
猜对了,被接受了,就节省了计算时间;但若猜错了,就会被拒绝,这样自然也就浪费了一些计算,同时还需要就猜错的地方进行就调整。
整体上,speculative decoding流程类似于“投机”(Speculative)行为中的“预先行动,再根据结果调整”。
2. 细节
现在我们来看一下speculative Decoding是如何评估的,也就是什么样才会接受,什么样又拒绝,拒绝后又如何重新采样。
2.1 接受
假设x采样自q(x),那么如果p(x)大,我们就接受这个。
这点可以这么理解,Mp是大一些的模型,它的准确性通常要高一些,q(x)<=p(x)表示的是比起Mq,Mp对生成的把握更高一些,那么这个x可以接受。
2.2 拒绝
反过来,如果p(x)< q(x),也就是说对于x,Mp的把握度低一些,即生成的有可能是错的。此时就以一定的概率拒绝x,这个概率为1-p(x)/q(x)。
因为p(x)< q(x),那么就有p(x)/q(x) < 1。并且,p(x)与 q(x)差距越大,p(x)/q(x)就越小,那么1-p(x)/q(x)就越大,拒绝的概率就越大。
2.3重新采样
当出现第一个拒绝的token,就需要重新采样并结束speculative Decoding的一轮了。
其中,重新采样需要调整对应位置的分布为:
。这里稍微注意下,前面的接受与拒绝,我们比较的是具体的token的概率值,这里调整的是token所在位置处的概率分布。
对于p(x)>= q(x)的那些x来说,p(x) - q(x) > 0;
对于p(x)< q(x)的x来说,p(x) - q(x) <= 0,再经过max(),值就置为零,那么这些token将永远不会被采样到。
通过这样的调整后再进行归一化,就得到了新的概率分布p’(x),再基于这个新分布来采样一个具体的token。
speculative decoding的一轮:
3 加速
一轮生成的期望token数
我们了解到执行一轮Speculative decoding,最多生成r +1个token,最少生成1个token。
那么平均情况下,执行一轮Speculative decoding,能生成多少个token呢?
3.1 接受率与它的期望值
βx<t(接受率):在Speculative decoding中,接受率所刻画的是,在给定x<t前缀的情况下,模型生成的token 被接受的概率。
α (平均接受率):β的期望值α=E(β),一定程度上衡量了Mq与Mp的近似/对齐程度(alignment),二者越接近,那么α越高。另外,应该是考虑了所有可能的前缀,也即
3.2 期望token数
Speculative decoding可能会遇到各种情况,比如;
第一个位置生成的token即x1~ Mp(prefix)就被拒绝;
第一个位置的token被接受,第二个位置的token即x2~ Mp(prefix)被拒绝
…
全部r个token都被接受。
假设β是一个随机变量并且是i.i.d,即独立同分布。那么Speculative decoding的过程可以描述如下:每次Mq生成一个token,以α的概率接受并继续生成;以1-α的概率拒绝并停止生成。
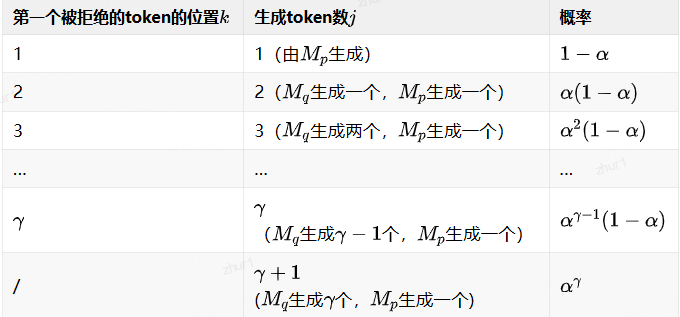
设第一个被拒绝的token的位置是k,那么每一种情况下生成的token数j的情况如下:
当k<=r了,Mq生成的前k-1个token全部被接受,第k个被拒绝,概率为ak-1(1-α)
Mp调整分布后重新采样生成第k个token;
k=r+1时,所有r个token都被接受,概率为ar,同时Mp额外生成第r+1个token。
有了期望token数的公式,图像就很容易画了(只需要给定a与r)。
显然有:
α越高,即两个模型越接近,接受概率越高,生成token数就起越超近r+1;
反过来若α越低,那么被拒绝的概率就越高,生成token数就越趋近于1
在α固定时,理论上增加了会增加一轮生成的token数。但是,如果α值过低,这个收益比就比较低(被拒绝的多了,很多计算就都浪费了)。所以,α对我们选择推测步数r是很重要的。
3.3 α如何计算
3.3.1 KL散度
3.3.2 散度的性质
同理p(x) <= q(x)
- 首先,DLK(p(x),q(x))是一个对称散度
- 并且,DLK在[0,1]区间
因为当p(x) = q(x),DLK = 0
- 另外,当p(x)与q(x)的支撑集不相交即p和q在任何可能的取值x上都不会同时赋予非零概率时(也即任意x,p(x)>0,有q(z)=0且任意x,q(x)>0,有p(x)=0)
3.3.3 计算α β
3.3.4 省了多少计算时间(加速效果)
假设有足够的计算资源支撑同时运行r+1个的Mp并行计算,且不产生其他额外的耗时。
这里先定义两个量:
当α>c,γ=1时,有
t2比t1耗时,确实实现了加速。也就是说,当接受率高于二者的耗时比,我们取推测步数 r=1就能实现加速,且加速比为
举个具体的例子,比如耗时比c=0.05,α>5%就能加速
若α趋近于1,那这个加速比将至少达到2=(1+1/1+0.05)
3.3.5 多了多少计算量(计算资源消耗)
虽然加速了,但是实际的计算量可能是增加了的。
首先,Speculative decoding一轮最多生成r+1个token,Mp并行执行r+1次。
假设token都被接受,那么平均生成每个token的计算量相当于执行一次Mp(忽略的计算量),所以没有增加计算。
反过来,如果有被拒绝的token,就产生了多余的计算,直观低也就是就少于r+1个token来平摊r+1次的计算量。也就是说生成单个token的计算量相比而言增加了。
下面就看看到底增加了多少计算量。同样先定义两个量:
那么,Speculative decoding执行一轮的计算量为
所以,单个token的平均计算量为:
访存上,在Speculative decoding中Mp是并行执行,所以模型的权重和KVcache可以一次性都读出来,就不用像纯粹的自回归要读
次(生成这么多个token)。所以访存次数缩减倍数即为这个数
3.3.6 α如何确定、Mq的选择
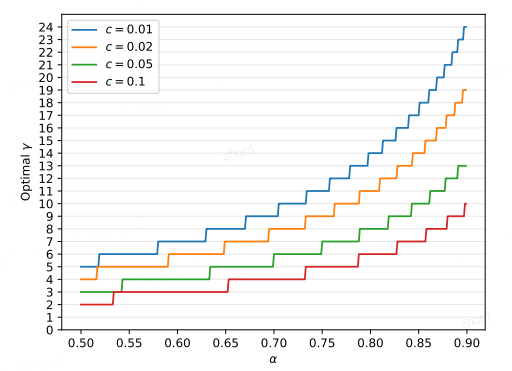
上面这幅图给出了在固定c和α时的最优r,在α比较低时r并不是越高越好,
比如我们就看绿色那条线(c=0.05):
当α=0.5时,最优r为3;
a=0.6时,最优y为4;而当α=0.9时,
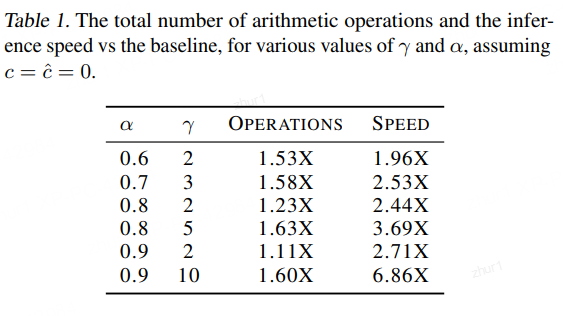
最优r超过了10。当r取10时,可以获得约6.86倍的加速(表1)。
但是,也不是说就直接取最优r了。
实际情况下,我们还需要去平衡加速比与计算量增加因子。
表1给出了一些量化结果,比如α=0.8, r取值从2增加到5时,加速比分别为从2.44提升到3.69,同时计算量也从1.23增加到1.63倍;
α=0.9, γ从2增加多到10时,加速比从2.71提升到6.86,而计算量也从1.11增大到1.60倍。
但是,实际情况中β是变化的,固定r不如动态调整r
动态计算β=Σ,min(p(x),q(x)),根据β值来调整r。
https://mp.weixin.qq.com/s/75KHpo-_JMGu8g7BGNYlzw





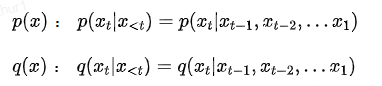
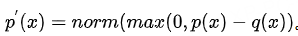

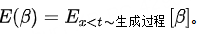
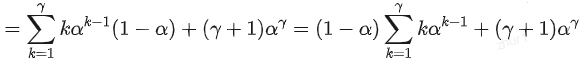
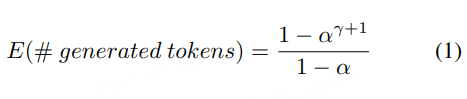


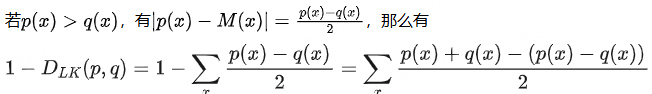
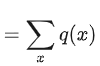
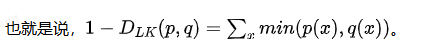
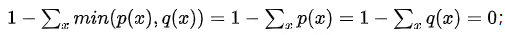
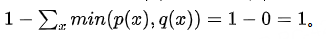

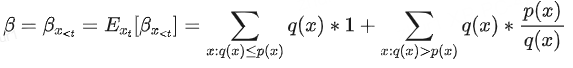
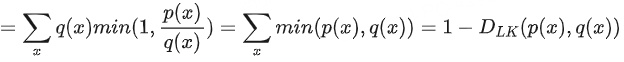
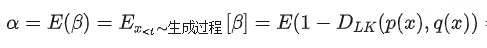
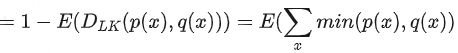
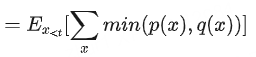



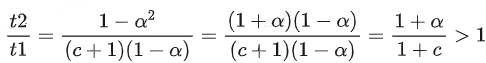
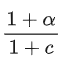

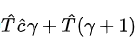
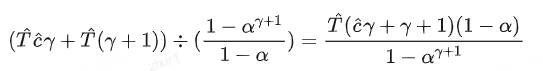
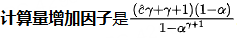
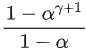
















 1754
1754

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








