汇总
余弦相似性 : 方向的量度
皮尔森相关系数(Pearson Correlation Coefficient),简称PCC
马修斯相关系数(Matthews Correlation Coefficient),简称MCC
Jaccard相似系数(Jaccard Coefficient)
Sørensen-Dice指数
Tanimoto系数(广义Jaccard相似系数)
对数似然相似度/对数似然相似率
互信息/信息增益,相对熵/KL散度
信息检索–词频-逆文档频率(TF-IDF)
词对相似度–点间互信息
余弦相似性:方向的量度
经常被用来抵消欧几里得距离的高维度问题。余弦相似性只是两个向量之间角度的余弦。如果将它们归一化为都有长度为1的向量,它的内积也相同。
两个方向完全相同的向量的余弦相似度为1,而两个方向截然相反的向量的相似度为-1,请注意,它们的大小并不重要,因为这是方向的量度。余弦相似度公式为:
缺点:大小不重要,方向重要
余弦相似性的一个主要缺点是不考虑向量的大小,只考虑其方向。在实际应用中,这意味着值的差异没有被完全考虑。以推荐系统为例,那么余弦相似性并没有考虑到不同用户之间的评分等级差异。
使用时机:高维且大小不重要
当我们有高维数据且向量的大小并不重要时,我们经常使用余弦相似度。对于文本分析来说,当数据用字数来表示时,这种测量方法是很常用的。
优点:取值在01之间,稳定指标
皮尔森相关系数(Pearson Correlation Coefficient)
定义:两个变量之间的皮尔逊相关系数
为两个变量之间的协方差(联合变异性)与标准差(个体变异性)的比率。
用于度量两个变量之间线性相关程度的统计量。
PCC值范围:[-1,1],PCC为1时表示完全正相关,为-1时表示完全负相关,为0时表示没有线性相关性。
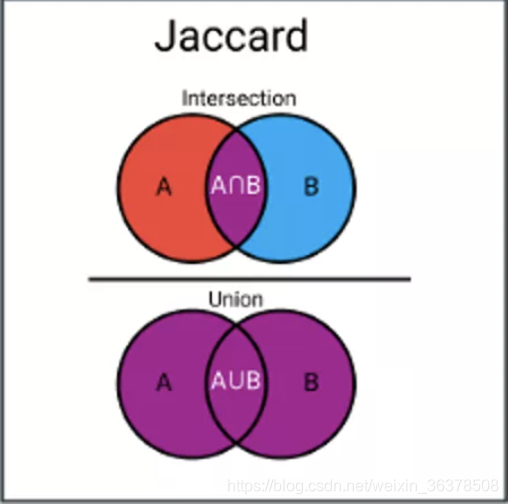
Jaccard相似度:
Jaccard指数(或称交集比联合)是一种用于计算样本集相似性和多样性的度量。它是交集的大小除以样本集的联合大小。
与Jaccard Coefficient相对应的是Jaccard 距离:d(X,Y) = 1 - Jaccard(X,Y);杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
缺点:
Jaccard指数的一个主要缺点是,它受数据大小的影响很大。大的数据集会对指数产生很大的影响,因为它可以在保持相似的交叉点的同时显著增加联合。
使用时机:
Jaccard指数经常用于使用二进制或二值化数据的应用中。当你有一个深度学习模型预测图像的片段时,例如,一辆汽车,Jaccard指数就可以用来计算给定真实标签的预测片段的准确度。同样,它也可以用于文本相似性分析,以衡量文档之间的选词重叠程度。因此,它可以用来比较模式的集合。
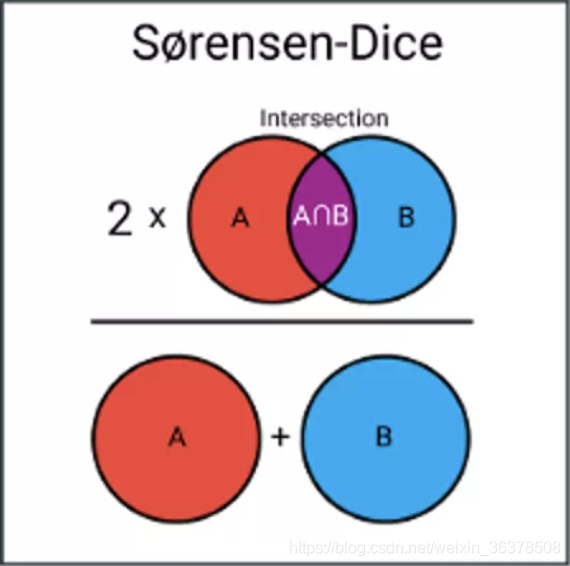
Sørensen-Dice指数: 两组之间的重叠百分比
Sørensen-Dice指数与Jaccard指数非常相似,因为它衡量样本集的相似性和多样性。
虽然它们的计算方法相似,但Sørensen-Dice指数更直观一些,因为它可以被看作是两组之间的重叠百分比,这个数值在0和1之间。Sørensen–Dice指数公式为:
缺点:
与Jaccard指数一样,它们都高估了集合的重要性,只有很少或没有TP(Truth Positive)值的正集合。因此,它可以求得多盘的平均分数。它将每个项目与相关集合的大小成反比加权,而不是平等对待它们。
使用时机:
与Jaccard指数相似,通常用于图像分割任务或文本相似性分析。
Tanimoto系数(广义Jaccard相似系数)
Tanimoto系数,也被称为谷本系数或广义Jaccard相似系数,元素的取值可以是实数。
起源于化学信息学领域,用于比较分子和分子之间的相似度。
其概念源于Jaccard系数,由Paul Jaccard在1901年首次提出,并在化学信息学中得到发展和应用。
原理
Tanimoto系数基于集合论的概念,用于量化两个集合的相似程度。
它通过比较两个集合的交集与并集的比例来确定它们的相似性。
其基本思想是,两个集合共享的元素越多,它们就越相似。
定义:Tanimoto系数 = |A ∩ B| / (|A| + |B| - |A ∩ B|)。
关系:如果我们的x,y都是二值向量,那么Tanimoto系数就等同Jaccard距离。
异同点
- 与Jaccard系数的异同:
Tanimoto系数是Jaccard系数在向量空间中的扩展。
当两个集合(或向量)的元素取值都是二值(0或1)时,Tanimoto系数就等同于Jaccard系数。
但在更一般的情况下(如元素取值非二值),Tanimoto系数能够提供更准确的相似度度量。- 与余弦相似度的异同:
余弦相似度是通过计算两个向量之间的夹角余弦值来衡量它们的相似度。
虽然Tanimoto系数和余弦相似度在形式上有些相似(都涉及向量的点积和模),但它们的分母不同,导致在不同场景下可能产生不同的结果。
一般来说,Tanimoto系数更适用于特征稀疏且取值非二值的情况。
优缺点
- 优点: 直观易懂,适用范围广,效果好
直观易懂:Tanimoto系数的定义简单直观,易于理解和解释。
适用范围广:不仅适用于二值数据,也适用于非二值数据,且能够处理稀疏特征。
效果好:在化学信息学、生物信息学等领域中,Tanimoto系数通常能够取得较好的相似度度量效果。- 缺点: 对噪声敏感,计算量大
对噪声敏感:当数据中存在噪声或异常值时,Tanimoto系数的计算结果可能会受到影响。
计算量大:当处理大规模数据集时,计算Tanimoto系数的计算量可能会很大。
应用场景
化学信息学:用于比较不同分子之间的相似度,进而进行分子聚类、分类、检索等操作。
生物信息学:用于比较不同基因、蛋白质等生物大分子之间的相似度,进而进行功能预测、分类等研究。
信息检索:用于衡量不同文档、网页等之间的相似度,进而进行文本分类、信息推荐等操作。
机器学习:在聚类、分类等任务中,可以使用Tanimoto系数作为相似度度量方法。
对数似然相似率
对于事件A和事件B,我们考虑两个事件发生的次数:
k11:事件A与事件B同时发生的次数
k12:B事件发生,A事件未发生
k21:A事件发生,B事件未发生
k22:事件A和事件B都未发生
rowEntropy = entropy(k11, k12) + entropy(k21, k22)
columnEntropy = entropy(k11, k21) + entropy(k12, k22)
matrixEntropy = entropy(k11, k12, k21, k22)
2 * (matrixEntropy - rowEntropy - columnEntropy)
互信息/信息增益
两个随机变量的相关性程度
互信息/信息增益:信息论中两个随机变量的相关性程度
相对熵/KL散度
又叫交叉熵,用来衡量两个取值为正数的函数(概率分布)的相似性
信息检索–词频-逆文档频率(TF-IDF)
《数学之美》中看到的TF-IDF算法,在网页查询(Query)中相关性以词频(TF)与逆文档频率(IDF)来度量查询词(key)和网页(page)的相关性;
网页中出现key越多,该page与查询结果越相关,可以使用TF值来量化
每个词的权重越高,也即一个词的信息量越大;
比如“原子能”就比“应用”的预测能力强,可以使用IDF值来量化,这里的IDF《数学之美》中说就是一个特定条件下关键词的概率分布的交叉熵。
词对相似度–点间相似度PMI
PMI (Pointwise mutual information,点间互信息)
PMI用于计算词语间的语义相似度
基本思想是统计两个词语在文本中同时出现的概率
概率越大,其相关性就越紧密,关联度越高。
两个词语word1与word2的PMI值计算公式如下式所示:





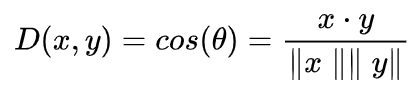


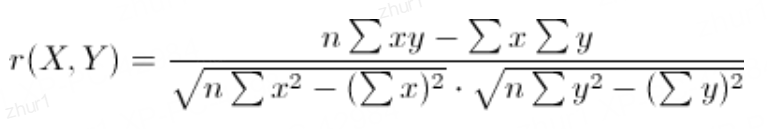
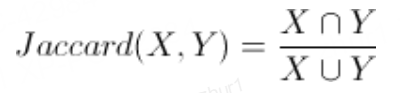
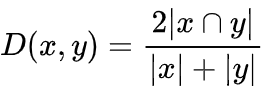
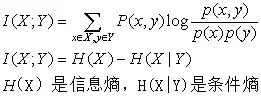
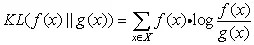

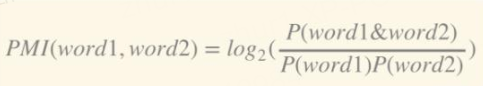
















 4012
4012

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








