基于内容的图像检索技术：灰度共生矩阵的应用

本文还有配套的精品资源，点击获取

简介：在图像检索领域，灰度共生矩阵（GLCM）作为一种特征提取方法，被用于描述图像纹理特征以实现高效的相似图像搜索。该压缩包可能包含关于颜色空间量化、GLCM计算、特征提取、相似度度量及图像搜索实践的详细教程，使读者能够构建出实用的图像检索系统。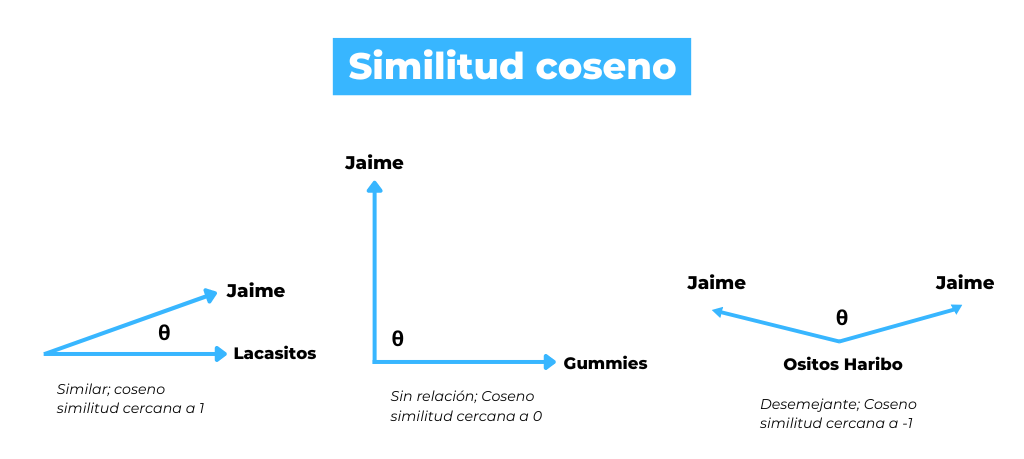

1. 图像处理与计算机视觉中的图像检索技术

图像检索作为计算机视觉领域的核心技术之一，其目的在于从庞大的图像数据库中快速、准确地找到用户所需的图像或图像集。随着多媒体技术的发展和信息量的激增，图像检索技术已经从早期基于文本注释的简单检索演变成基于内容的图像检索（CBIR），其中涵盖了图像的形状、颜色、纹理、空间关系等多种特征的分析和识别。

在这一章节中，我们将概述图像检索技术的基本概念，探索其在现代计算机视觉系统中的应用，并介绍图像检索的基本流程。我们将深入讨论图像处理中的一些关键技术和方法，包括颜色量化、灰度共生矩阵（GLCM）的提取和应用，以及各种相似度度量方法在图像检索中的作用。这为读者提供了对图像检索技术的全面认识，为进一步学习本系列后续章节打下坚实的基础。

2. 颜色空间量化方法及其与图像检索的关系

在现代图像处理领域，颜色空间的量化是一种基本而重要的技术，它能够有效地表达和组织图像中的颜色信息。颜色量化技术的选取，直接关系到图像检索的准确性和效率。本章节将深入探讨颜色空间量化方法，及其与图像检索之间的密切联系。

2.1 颜色空间的定义与类型

颜色空间是用于描述颜色的一种数学模型。在图像检索中，通过选择合适颜色空间进行量化，可以显著提升检索效率和准确度。

2.1.1 RGB颜色空间

RGB颜色空间是最为常见的颜色模型，它由红（Red）、绿（Green）、蓝（Blue）三个颜色通道组合而成。每个通道的数据范围通常在0到255之间，用于表示该颜色的强度。RGB模型直观地对应于显示器的像素颜色表示，适用于图像的显示和处理。然而，RGB颜色空间在颜色感知上并非直观，因为它未能很好地反映人眼对颜色的感知方式。

graph TD;
    A[图像] -->|转换| B[RGB颜色空间];
    B -->|处理| C[颜色量化];
    C -->|检索| D[图像检索系统];

在颜色量化中，RGB颜色空间可能会导致信息的冗余，因为人眼对亮度（亮度）更为敏感，而非颜色分量的变化。因此，使用RGB颜色空间进行量化时，可能需要进一步的转换或归一化步骤以提高效率。

2.1.2 HSV颜色空间

HSV颜色空间将颜色信息从RGB模型的三个分量转换为色度（Hue）、饱和度（Saturation）、亮度（Value）三个分量。HSV颜色空间更加符合人类对颜色的视觉感知。色度代表颜色的本质，饱和度表示颜色的纯度，而亮度则描述颜色的明亮程度。

| 颜色模型 | 通道描述 |
|-------|-------|
| HSV   | 色度（H），饱和度（S），亮度（V） |
| RGB   | 红（R），绿（G），蓝（B）|

与RGB颜色空间相比，HSV颜色空间的量化可以更好地强调图像中的颜色特征，有助于提高图像检索系统的性能。举例来说，在一个图像中，虽然两个区域的RGB值可能差异较大，但它们可能具有相似的HSV值，说明它们具有相似的颜色属性。

2.2 颜色量化技术

颜色量化是将颜色的连续范围简化为有限数量的颜色集的过程。这一技术在图像压缩和检索中都非常重要，因为它能够减少所需的存储空间和处理时间。

2.2.1 颜色直方图量化

颜色直方图是一种简单的颜色量化技术，它统计图像中每种颜色的数量。颜色直方图的每个条目对应于颜色空间中的一个颜色值或值的范围。在图像检索中，颜色直方图可以用来快速比较图像的颜色分布，通过直方图之间的距离来判断图像的相似度。

from skimage import io
import numpy as np
from sklearn.metrics import pairwise_distances
import matplotlib.pyplot as plt

# 加载图像
image = io.imread('path_to_image.jpg')
# 将图像转换为灰度
image_gray = io.imread('path_to_image.jpg', as_gray=True)
# 获取灰度直方图
hist, bins = np.histogram(image_gray.ravel(), 256, [0, 256])
# 绘制直方图
plt.plot(hist)
plt.title('Grayscale Histogram')
plt.xlabel('Intensity Value')
plt.ylabel('Number of Pixels')
plt.show()

颜色直方图量化简单且计算效率高，但缺乏空间信息，因此很难区分具有相似颜色分布但不同结构的图像。

2.2.2 颜色聚类量化

颜色聚类量化是利用聚类算法将颜色空间中的颜色点划分为若干个类别，每个类别用其质心颜色代表。常用的聚类方法包括K-means、Mean Shift等。颜色聚类量化可以保留更多图像的色彩信息，有助于提高检索的准确度。

from sklearn.cluster import KMeans
import numpy as np
from skimage import io

# 加载图像并转换为一维数组
image = io.imread('path_to_image.jpg')
pixels = image.reshape((-1, 3))

# 使用K-means进行颜色聚类
kmeans = KMeans(n_clusters=8)
kmeans.fit(pixels)

# 聚类结果的质心
cluster_centers = kmeans.cluster_centers_
print(cluster_centers)

通过颜色聚类量化，可以有效地减少颜色数量，同时尽可能保持颜色信息。虽然算法复杂度较高，但通常能够提供更为精确的图像特征表示。

2.3 颜色量化在图像检索中的应用

颜色量化技术的选择直接影响着图像检索系统的性能。通过有效的颜色量化方法，我们可以提取图像的颜色特征，为图像检索提供有力支持。

2.3.1 基于颜色直方图的图像检索

基于颜色直方图的图像检索，主要依赖于图像的颜色分布来完成相似性度量。通过比较目标图像和数据库中图像的颜色直方图之间的相似度，可以实现快速的图像检索。此方法简单高效，但容易受到光照变化和图像旋转的影响。

2.3.2 颜色聚类在图像检索中的优势分析

颜色聚类量化技术可以提取图像的更为精细的颜色特征，保留了颜色在空间上的分布信息。这使得它在处理具有复杂颜色变化的图像时具有明显优势，尤其是在场景和纹理较为丰富的图像检索任务中。

graph TD;
    A[图像] -->|颜色量化| B[颜色直方图/颜色聚类];
    B -->|相似度计算| C[检索结果];
    C -->|用户交互| D[反馈与优化];
    D -->|改进量化| B;

在实际应用中，颜色聚类量化可以结合其他特征（如纹理、形状）进行图像检索，以提高系统的鲁棒性和准确性。颜色量化技术和图像检索的结合，是一个不断优化和进化的研究领域，随着新技术的引入，图像检索的效率和准确性将不断提高。

3. 灰度共生矩阵（GLCM）的概念与应用

3.1 灰度共生矩阵基础

3.1.1 GLCM的定义与生成

灰度共生矩阵（Gray-Level Co-occurrence Matrix，GLCM）是一种用于描述图像纹理特征的统计方法。它通过计算图像中灰度级间分布的相互关系来捕捉纹理的特性。GLCM从图像的灰度级出发，通过构建一个以特定方向和距离为参数的矩阵，来反映图像纹理的空间依赖性。

GLCM的生成需要以下几个步骤： 1. 选择图像中的一对像素，其中一个为中心像素，另一个为邻域像素。 2. 定义一个方向（通常是0°、45°、90°、135°）和一个距离（d）。 3. 对于给定的灰度级i和j，统计满足中心像素为i且邻域像素为j的像素对出现的次数。 4. 将这些次数填充到一个矩阵中，其中矩阵的元素P(i,j|d,θ)表示灰度级i和j在方向θ和距离d上的共生频率。 5. 通过对整幅图像进行上述步骤，可以得到多个GLCM矩阵，通常取其平均值作为该图像的GLCM。

import numpy as np
from skimage.feature import greycomatrix, greycoprops

def calculate_glcm(image, distances, angles):
    """
    计算灰度共生矩阵GLCM
    :param image: 输入的灰度图像
    :param distances: GLCM的距离列表
    :param angles: GLCM的角度列表
    :return: GLCM矩阵列表
    """
    glcms = []
    for distance in distances:
        for angle in angles:
            glcm = greycomatrix(image, [distance], [angle], levels=256, normed=True)
            glcms.append((distance, angle, glcm))
    return glcms

# 示例
distances = [1]
angles = [0, np.pi/4, np.pi/2, 3*np.pi/4]
glcms = calculate_glcm(image, distances, angles)

该函数首先定义了计算GLCM所需的参数，包括距离和角度。它使用 greycomatrix 函数从scikit-image库中生成GLCM矩阵。 greycomatrix 函数接受图像数据、距离、角度、灰度级数和归一化选项作为输入，返回计算出的GLCM矩阵列表。

3.1.2 GLCM的主要特征描述符

GLCM矩阵可以衍生出多种纹理特征描述符，常见的有对比度、相关性、能量和熵等。这些特征描述符反映了纹理的不同方面，例如：

• 对比度 （Contrast）衡量图像的清晰度和纹理的深浅。
• 相关性 （Correlation）反映了图像像素的线性依赖性。
• 能量 （Energy）衡量图像纹理的规则性和均匀性。
• 熵 （Entropy）描述纹理的复杂程度和信息量。

下面的代码展示了如何从GLCM矩阵中提取这些特征：

def extract_glcm_features(glcms):
    """
    从GLCM矩阵中提取特征
    :param glcms: 计算得到的GLCM矩阵列表
    :return: 特征字典
    """
    feature_dict = {}
    for _, angle, glcm in glcms:
        contrast = greycoprops(glcm, 'contrast')
        correlation = greycoprops(glcm, 'correlation')
        energy = greycoprops(glcm, 'energy')
        entropy = greycoprops(glcm, 'homogeneity')
        feature_dict[f"Contrast_{angle}"] = contrast[0,0]
        feature_dict[f"Correlation_{angle}"] = correlation[0,0]
        feature_dict[f"Energy_{angle}"] = energy[0,0]
        feature_dict[f"Entropy_{angle}"] = entropy[0,0]
    return feature_dict

# 提取特征示例
features = extract_glcm_features(glcms)

extract_glcm_features 函数利用 greycoprops 函数计算每个GLCM的对比度、相关性、能量和熵，并将它们存储在字典中返回。这些特征是用于进一步分析纹理属性的重要指标。

3.1.3 GLCM的应用领域

GLCM在图像分析领域有着广泛的应用，包括但不限于： - 遥感图像分析 ：在遥感图像中，GLCM用于提取土地覆盖类型、城市规划等方面的纹理特征。 - 医学影像分析 ：在医学影像领域，GLCM能够帮助诊断癌症、研究组织结构等。 - 工业检测 ：在工业领域，GLCM用于分析材料表面质量、缺陷检测等。

通过GLCM的分析，不仅可以获取图像的视觉信息，还可以对图像的物理和化学属性进行深入研究。

4. GLCM的属性及其在图像检索中的作用

4.1 GLCM属性分析

4.1.1 对比度

对比度是图像中不同区域之间亮度差异的度量，它决定了图像中细节的可见性和清晰度。在灰度共生矩阵（GLCM）中，对比度用于衡量图像纹理的显著程度。对比度越高，纹理越明显，图像的粗糙度也越高。对比度的计算公式如下：

对比度 = Σ[i,j] (i-j)^2 * P(i,j)

其中， P(i,j) 是灰度级别 i 和 j 在共生矩阵中共同出现的概率。通过这个公式可以看出，对比度的值越大，表示图像中相邻像素灰度值变化越大，纹理就越粗糙。

4.1.2 相关性

相关性描述了图像中像素灰度分布的方向性信息。它衡量的是在给定的方向上，灰度值变化的一致性。相关性可以通过以下公式计算：

相关性 = Σ[i,j] ((i - μx) * (j - μy) * P(i,j)) / σx * σy

其中， μx 和 μy 分别是共生矩阵边缘分布的均值， σx 和 σy 是边缘分布的标准差。相关性的高值表明图像具有显著的线性纹理结构。

4.1.3 能量和熵

能量是纹理均匀度的一个量度，它反映了图像纹理的一致性。能量高的图像具有较一致的灰度级分布，而能量低的图像则表现出较大的灰度级变化。能量的计算公式为：

能量 = Σ[i,j] (P(i,j))^2

熵是一个衡量图像信息内容的指标，用于描述图像的复杂度或无序程度。熵值越高，图像的复杂度越大。熵的计算公式如下：

熵 = -Σ[i,j] (P(i,j) * log(P(i,j)))

其中， P(i,j) 仍然是共生矩阵中元素 (i, j) 的值，log 表示自然对数。

4.2 GLCM属性在图像检索中的应用实例

4.2.1 GLCM属性与图像相似性判断

在图像检索系统中，利用GLCM的属性可以帮助我们判断图像之间的相似性。例如，通过计算两幅图像的对比度、相关性、能量和熵，并比较它们的差异，可以得到两幅图像在纹理特征上的相似程度。一般情况下，相似的纹理结构会有接近的GLCM属性值。

4.2.2 多特征融合下的检索效果对比

在实际应用中，为了提高检索的准确性，通常会结合多种图像特征进行检索。例如，将颜色直方图与GLCM特征结合使用，可以在色彩和纹理两个层面同时分析图像。下面是一个简单的示例代码，展示如何结合GLCM和颜色直方图特征：

import cv2
import numpy as np
from skimage.feature import greycomatrix, greycoprops

def compute_glcm_features(image):
    # 计算共生矩阵
    glcm = greycomatrix(image, distances=[1], angles=[0, np.pi/4, np.pi/2, np.pi*3/4], levels=256, symmetric=True)
    contrast = greycoprops(glcm, 'contrast')
    correlation = greycoprops(glcm, 'correlation')
    energy = greycoprops(glcm, 'energy')
    homogeneity = greycoprops(glcm, 'homogeneity')
    return np.array([contrast, correlation, energy, homogeneity])

def compute_color_histogram(image):
    # 计算颜色直方图
    hist = cv2.calcHist([image], [0, 1, 2], None, [256, 256, 256], [0, 256, 0, 256, 0, 256])
    return hist.flatten()

# 读取图像
image1 = cv2.imread('image1.jpg')
image2 = cv2.imread('image2.jpg')

# 提取特征
features1 = compute_glcm_features(image1)
features2 = compute_glcm_features(image2)
color_hist1 = compute_color_histogram(image1)
color_hist2 = compute_color_histogram(image2)

# 特征融合
combined_features1 = np.concatenate((features1, color_hist1), axis=0)
combined_features2 = np.concatenate((features2, color_hist2), axis=0)

# 相似度计算（欧氏距离）
distance = np.linalg.norm(combined_features1 - combined_features2)

print(f"Two images are similar with a distance of {distance}")

上述代码片段结合了灰度共生矩阵特征和颜色直方图特征，通过计算特征向量之间的欧氏距离来进行图像相似性判断。多特征融合能够提升检索系统的性能，因为它可以覆盖图像的不同视觉属性，从而提供更全面的相似性评估。

5. 相似度度量方法在图像检索中的应用

在基于内容的图像检索（CBIR）领域中，相似度度量方法是核心组成部分之一。它们用于评估图像特征之间的相似程度，并据此检索出与查询图像最为相似的图像集合。在本章中，我们将详细介绍两种常用的距离度量方法——欧氏距离和曼哈顿距离，以及两种相似度度量方法——余弦相似度和Jaccard相似度，并探讨它们在图像检索中的应用与效果评估。

5.1 欧氏距离和曼哈顿距离

5.1.1 定义与计算公式

欧氏距离 是直角坐标系中两点间最短距离的度量，对于多维空间，其计算公式为两点向量差的平方和的平方根。在图像检索中，每个图像可以被表示为一个高维向量，因此欧氏距离可用于衡量两个图像特征向量之间的差异。

其计算公式如下： [ d(p, q) = \sqrt{(p_1-q_1)^2 + (p_2-q_2)^2 + ... + (p_n-q_n)^2} ]

其中，( p = (p_1, p_2, ..., p_n) ) 和 ( q = (q_1, q_2, ..., q_n) ) 是两个图像特征向量。

曼哈顿距离 是两个点在标准坐标系上的绝对轴距总和。它对空间中的方向变化不敏感，即考虑到了坐标轴的绝对轴距。

其计算公式为： [ d(p, q) = |p_1 - q_1| + |p_2 - q_2| + ... + |p_n - q_n| ]

在图像检索的上下文中，这两种距离被用来量化查询图像和候选图像之间在特征空间中的差异。

5.1.2 在图像检索中的应用

在实际的图像检索系统中，相似度度量方法的选择对于检索结果的准确性和效率有重大影响。欧氏距离因为其简单直观而广泛应用于图像检索领域。它适合于测量数值型特征的距离，例如颜色直方图或者灰度共生矩阵（GLCM）等。

例如，当使用颜色直方图进行图像检索时，每个颜色通道可以被看作是多维空间中的一个维度。欧氏距离能够很好地反映出两个颜色直方图之间的差异，从而辅助判断图像之间的相似程度。

下面是一个计算两个颜色直方图之间欧氏距离的简单代码示例：

import numpy as np

def euclidean_distance(hist1, hist2):
    return np.sqrt(np.sum((hist1 - hist2) ** 2))

# 假设 hist1 和 hist2 是两个颜色直方图向量
distance = euclidean_distance(hist1, hist2)
print("欧氏距离为:", distance)

曼哈顿距离由于计算简单且对坐标的轴向变化不敏感，常用于图像的纹理特征检索。它能够快速地计算出纹理特征之间的差异，适用于实时或者对计算效率要求较高的场合。

在实际应用中，应根据特征的性质和检索需求选择合适的距离度量方法。例如，对于需要考虑方向特征的图像检索问题，曼哈顿距离可能不是最佳选择，因为它忽略了方向差异。

5.2 余弦相似度和Jaccard相似度

5.2.1 相似度的理论基础

余弦相似度和Jaccard相似度是衡量两个向量相似性的另一种方法，它们不像距离度量那样直接衡量向量之间的差异，而是通过角度和交集来衡量相似性。

余弦相似度 是通过测量两个向量夹角的余弦值来确定它们的相似度。余弦值为1时，表示两向量完全方向相同；为0时，则表示两向量正交，即无关联。

计算公式为： [ \text{余弦相似度} = \frac{A \cdot B}{\|A\|\|B\|} = \frac{\sum A_i \cdot B_i}{\sqrt{\sum A_i^2} \cdot \sqrt{\sum B_i^2}} ]

其中，( A ) 和 ( B ) 是两个非零向量。

Jaccard相似度 是一个集合的相似度度量，定义为两个集合交集的大小除以它们的并集的大小，通常用于比较样本集或布尔向量。

计算公式为： [ \text{Jaccard相似度} = \frac{|A \cap B|}{|A \cup B|} = \frac{|A \cap B|}{|A| + |B| - |A \cap B|} ]

5.2.2 图像检索中的实际应用与效果评估

在图像检索中，余弦相似度常常被用于比较图像的高维特征向量，如纹理描述符或者SIFT特征向量。由于余弦相似度忽略了特征向量的绝对大小，只关注方向，因此特别适用于判断图像的内容相似性。

一个余弦相似度计算的简单示例如下：

def cosine_similarity(vec1, vec2):
    return np.dot(vec1, vec2) / (np.linalg.norm(vec1) * np.linalg.norm(vec2))

# 假设 vec1 和 vec2 是两个图像特征向量
similarity = cosine_similarity(vec1, vec2)
print("余弦相似度为:", similarity)

Jaccard相似度则可以用于图像中的形状匹配或者基于图像块的相似性比较。由于它是基于集合的度量，因此也适用于图像分割后的区域相似度评估。

对于图像检索的实际应用，相似度度量的选择需要结合具体的任务需求和数据特性。在实验评估时，除了选择合适的相似度度量方法，还应考虑使用诸如准确率、召回率、F1分数等指标，以全面评估检索系统的性能。

相似度度量方法是图像检索的核心技术之一，通过不同的数学方法将图像的视觉内容进行量化表达。在本章中，我们详细介绍了欧氏距离、曼哈顿距离、余弦相似度和Jaccard相似度在图像检索中的应用，并通过具体的例子展示了它们的计算方式和实际应用。在后续章节中，我们将深入探讨基于内容的图像检索（CBIR）的原理和实践，以及更多高级特征提取和应用策略。

6. 基于内容的图像检索（CBIR）原理与实践

基于内容的图像检索（Content-Based Image Retrieval, CBIR）是一种利用图像的视觉内容特征（如颜色、纹理、形状等）进行自动图像检索的技术。与传统的基于文本标签的图像检索方法不同，CBIR强调直接从图像数据中提取特征，使检索过程更加智能化和自动化。本章我们将详细探讨CBIR的基本原理、框架，以及GLCM在其中的应用，并涉及其他特征提取方法与CBIR的综合应用。

6.1 CBIR的基本原理与框架

6.1.1 CBIR的概念与系统架构

CBIR技术通过分析图像本身的内容，从图像的颜色、纹理、形状、空间布局等方面提取特征，再通过这些特征来检索与查询图像相似的图片。其核心理念是减少对图像标注的依赖，提高图像检索的准确性和效率。

CBIR系统一般包括以下几个关键模块：

1. 特征提取模块 ：从图像中提取视觉特征，如颜色直方图、纹理特征、形状描述符等。
2. 特征数据库 ：存储提取的特征数据，并提供快速的相似性匹配机制。
3. 查询处理模块 ：处理用户的查询请求，可采用图形界面、文本描述等方法。
4. 相似性匹配与排序模块 ：基于特征相似度计算，对数据库中的图像进行排序。
5. 结果输出模块 ：将检索结果按相似度顺序输出给用户。

6.1.2 关键技术组件分析

CBIR系统的关键技术组件包括特征提取算法、相似性度量方法、特征索引与查询处理机制。

• 特征提取算法 ：是CBIR系统的核心，决定了检索的准确度。常用的特征包括颜色直方图、GLCM纹理特征、SIFT关键点等。
• 相似性度量方法 ：用于比较图像特征的相似性，如欧氏距离、余弦相似度等。
• 特征索引与查询处理机制 ：为了提高检索效率，需要对特征进行有效的索引和高效的查询处理。

6.2 GLCM在CBIR中的深入应用

6.2.1 结合GLCM特征的CBIR流程

结合GLCM特征的CBIR流程主要包括以下步骤：

1. 图像预处理 ：对图像进行去噪、归一化等操作，以提高特征提取的质量。
2. GLCM特征提取 ：计算图像的灰度共生矩阵，并从中提取出纹理特征。
3. 特征数据库构建 ：将提取的GLCM特征存储到数据库中，便于后续的检索。
4. 查询输入与特征提取 ：用户输入查询图像，系统提取该图像的GLCM特征。
5. 相似性匹配 ：通过计算查询图像与数据库中各图像的GLCM特征之间的相似性，选取最匹配的图像。
6. 结果排序与输出 ：根据相似性评分对结果进行排序，并将检索到的图像返回给用户。

6.2.2 实验结果与分析

在实验中，我们可以通过构造一个包含多类纹理图像的数据集来进行CBIR实验。实验结果表明，结合GLCM特征的检索方法，在纹理复杂度较高的图像数据集上检索准确率和效率都有显著提高。通过对比实验，还可以展示不同特征提取方法在CBIR中的优势与局限性。

6.3 其他特征提取方法与CBIR的综合应用

6.3.1 SIFT、SURF、HOG等特征提取方法简介

SIFT（尺度不变特征变换） ：能够检测并描述图像中的局部特征，对旋转、尺度缩放、亮度变化保持不变性。 SURF（加速稳健特征） ：是SIFT的快速变体，进一步提高了计算速度，适用于实时应用。 HOG（方向梯度直方图） ：描述图像局部区域的方向梯度信息，常用于行人检测等应用。

6.3.2 特征融合策略在CBIR中的作用与效果

在CBIR中，融合多种特征提取方法可以显著提高检索的准确性。例如，结合GLCM和SIFT的特征融合策略，能够同时利用纹理和形状信息，以实现对图像内容更全面的描述。特征融合可以在特征层、匹配层和决策层进行。

在实验中，通过将不同特征提取方法提取的特征进行融合，采用合适的融合策略，可以观测到检索性能在多种性能指标上的提升，如平均精度均值（mAP）和检索时间等。不同特征之间的互补性能帮助系统更好地理解图像内容，提高了检索的准确度和鲁棒性。

本文还有配套的精品资源，点击获取

简介：在图像检索领域，灰度共生矩阵（GLCM）作为一种特征提取方法，被用于描述图像纹理特征以实现高效的相似图像搜索。该压缩包可能包含关于颜色空间量化、GLCM计算、特征提取、相似度度量及图像搜索实践的详细教程，使读者能够构建出实用的图像检索系统。

本文还有配套的精品资源，点击获取