《统计学习方法》——第四章朴素贝叶斯及C++实现

最新推荐文章于 2024-11-17 21:19:36 发布

李滚滚

最新推荐文章于 2024-11-17 21:19:36 发布

阅读量535

点赞数

CC 4.0 BY-SA版权

分类专栏：机器学习统计学习方法学习总结与实现文章标签：统计学习方法

本文链接：https://blog.youkuaiyun.com/weixin_35479108/article/details/84942332

机器学习同时被 2 个专栏收录

21 篇文章

订阅专栏

统计学习方法学习总结与实现

12 篇文章

订阅专栏

本文深入解析了朴素贝叶斯分类器的工作原理，包括其先验概率和条件概率的计算方法，以及如何利用这些概率进行分类预测。通过一个C++实现的例子，展示了从数据加载到预测的完整流程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Input: 特征向量
Output : 实例类别
可用于多分类，属于生成模型，先估计X,Y的联合概率分布P（X,Y），再计算条件概率P(Y|X)
朴素贝叶斯法和朴素贝叶斯估计是两种不同的概念
朴素贝叶斯法（model)---->参数估计
$参数估计=\left\{ \begin{aligned} 最大似然估计\\ 贝叶斯估计 \\ \end{aligned} \right.$ 改进原因，如果某一个要估计的P为0，例如NLP应用中，某个词向量出现的次数为0，影响后验概率的计算，因此使用贝叶斯估计方法。最大似然估计，最大可能性估计。

强条件独立性的基本假设

用于分类的特征在类确定的条件下都是条件独立的,在这种强条件独立性假设下，可以省去每种特征向量的参数估计，复杂度降低，但是会降低估计的准确性。
$P(X=x∣Y=Ck)=P(X(1)=x(1),X(2)=x(2),⋯ ,X(n)=x(n)∣Y=Ck)=∏i=1nP(X(i)=x(i)∣Y=Ck)P(X=x|Y=C_k)=P(X^{(1)} =x^{(1)},X^{(2)} =x^{(2)},\cdots,X^{(n)} =x^{(n)}|Y=C_k)\\ =\prod_{i=1}^{n}P(X^{(i)} =x^{(i)}|Y=C_k)$

P(X,Y)是怎么求出来的呢？

${贝叶斯定理P(X,Y)=P(X∣Y)P(Y)强条件假设P(X∣Y)=P(X=x∣Y=Ck)\left\{ \begin{aligned} 贝叶斯定理 P(X,Y)=P(X|Y)P(Y)\\ 强条件假设 P(X|Y) = P(X=x|Y=Ck) \\ \end{aligned} \right.$ 根据前面强条件假设可以求得P(X|Y),P(Y)也可求
所以 $P(Y=Ck∣X=x)=P(X,Y)P(Y)=P(X=x∣Y=Ck)P(Y=Ck)∑kP(X=x∣Y=Ck)P(Y=Ck)P(Y=C_k|X=x)=\frac{P(X,Y)}{P(Y)} =\frac{P(X=x|Y=C_k)P(Y=C_k)}{\sum_{k}P(X=x|Y=C_k)P(Y=C_k)}$ $=P(Y=Ck)∏i=1nP(X(i)=x(i)∣Y=Ck)∑kP(Y=Ck)∏jP(X(j)∣Y=Ck)=\frac{P(Y=C_k)\prod_{i=1}^{n}P(X^{(i)} =x^{(i)}|Y=C_k)} {\sum_{k}P(Y=C_k)\prod_{j}P(X^{(j)}|Y=C_k)}$
因为分母部分都是一样的，所以最后只需 $y=argmaxCkP(Y=Ck)∏i=1nP(X(i)=x(i)∣Y=Ck)y=argmax_{C_k}P(Y=C_k)\prod_{i=1}^{n}P(X^{(i)} =x^{(i)}|Y=C_k)$

极大似然估计：

$P(Y=Ck)=∑i=1NI(yi=Ck)NP(Y=C_k)=\frac{\sum_{i=1}^{N}I(y_i=C_k)}{N}$ $P(X(j)=ajl∣Y=Ck)=∑i=1NI(XI(j)=ajl,yi=Ck)∑i=1NI(yi=Ck)P(X^{(j)} =a_{jl}|Y=C_k)=\frac{\sum_{i=1}^{N}I(X_I^{(j)}=a_{jl},y_i=C_k)}{\sum_{i=1}^{N}I(y_i=C_k)}$
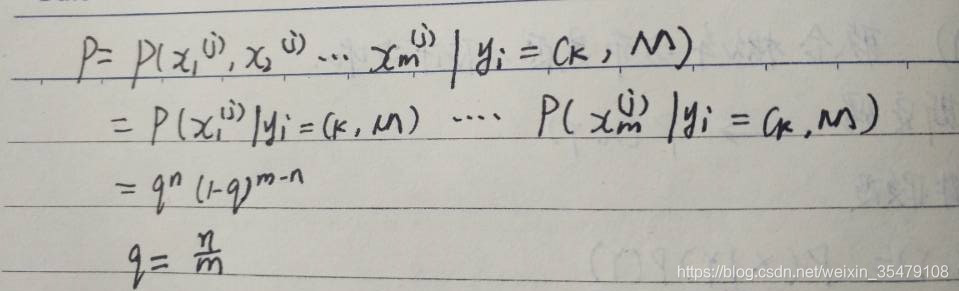
在这里插入图片描述

贝叶斯估计：

$P(Y=Ck)=∑i=1NI(yi=Ck)+λN+kλP(Y=C_k)=\frac{\sum_{i=1}^{N}I(y_i=C_k)+\lambda}{N+k\lambda}$ $P(X(j)=ajl∣Y=Ck)=∑i=1NI(XI(j)=ajl,yi=Ck)+λ∑i=1NI(yi=Ck)+SjλP(X^{(j)} =a_{jl}|Y=C_k)=\frac{\sum_{i=1}^{N}I(X_I^{(j)}=a_{jl},y_i=C_k)+\lambda}{\sum_{i=1}^{N}I(y_i=C_k)+S_j\lambda}$ $S_j表示每类特征的可能性$ $
在这里插入图片描述

按照书上例子以及算法流程使用C++实现如下：

#include <iostream> 
#include <vector> 
#include<fstream> 
using namespace std;c
onst int MaxNum = 20;
struct DataSet
{
    vector<double> samples;
    int labels;
}data[MaxNum];
class Bayes
{
public:    
/**加载数据**/
    int loadData()
    {
        fstream f ;
        int countNum = 0;
        f.open("data.txt");
        int i = 0; double temp1,temp2;        while(!f.eof())
        {
            f>>temp1>>temp2>>data[i].labels;
            data[i].samples.push_back(temp1);
            data[i].samples.push_back(temp2);
            i++;
            countNum++;
        }
        f.close();
        return countNum;
    }    
    /**指示函数,如果A==B 返回1，若果不相等返回0**/
    bool Indication_function(double a,double b)
    {
        if(a==b)
            return true;
        else
            return false;
    }
    /**找到一个向量中不同的数值，并返回向量**/
    vector<int> find_different(vector<int> arg)
    {
        int K = arg.size();
        vector<int> Ck;
        Ck.push_back(arg[0]);
        int flag =0;
        for (int i=1;i<K;i++)
        {
            for(int j =0;j<Ck.size();j++)
            {
                if(Indication_function((double)arg[i],(double)Ck[j]))
                    break;
                else
                    flag++;
            }
            if(flag == Ck.size())
            {
                Ck.push_back(arg[i]);
            }
            flag = 0;
        }
        return Ck;
    }    
    /**函数重载或者模板类会好一些**/
    vector<double> find_different(vector<double> arg)
    {
        int K = arg.size();
        vector<double> Ck;
        Ck.push_back(arg[0]);
        int flag =0;
        for (int i=1;i<K;i++)
        {
            for(int j =0;j<Ck.size();j++)
            {
                if(Indication_function((double)arg[i],(double)Ck[j]))
                    break;
                else
                    flag++;
            }
            if(flag == Ck.size())
            {
                Ck.push_back(arg[i]);
            }
            flag = 0;
        }
        return Ck;
    }
    /**计算所有的样本属于某一类的概率，先验概率**/
    vector<double> Priori_Probability(vector<int> Ck,DataSet *data,int N)
    {
        int k = Ck.size();
        vector<double> pp;
        int countNum = 0;
        for(int i=0;i<k;i++)
        {
            for(int j=0;j<N;j++)
            {
                if(Indication_function(data[j].labels,Ck[i]))
                    countNum++;
            }
            pp.push_back(countNum/(double)N);
            countNum = 0;
        }
        return pp;
    }    
    /**找到不同的特征有多少不同的取值**/
    vector<vector<double>> find_features(DataSet data[],int N)
    {
        int K=2; //data.samples.size();
        vector<vector<double>> features(K);
        vector<double> a;
        for(int k=0;k<features.size();k++)
        {
            features[k].resize(K);
        }
        vector<double> temp;
        for(int i=0;i<K;i++)
        {
            for(int j = 0;j<N;j++)
            {
                temp.push_back(data[j].samples[i]);
            }
            features[i] = find_different(temp);
            temp.clear();
        }
        return features;
    }
    /**计算条件概率
    输入为：类别种类
             特征及其取值
             样本
             样本个数
    **/
    vector<vector<vector<double>>> Conditional_Probability(vector<int> Ck,vector<vector<double>> features,DataSet *data,int N)
    {
        int ck_N = Ck.size();//ck_N是类别的不同
        int feature_k = features.size();
        //定义每一类的坟墓个数
        vector<int> fenmu(ck_N);
        for(int k=0;k<ck_N;k++)
        {
            fenmu.push_back(0);//分母的计算应该是对的，但是分子可能有问题
        }        //定义返回结果，每一类中不同特征所占的比例数，也就是条件概率
        vector<vector<vector<double>>> res(ck_N);
        for(int n=0;n<ck_N;n++)
        {
            res[n].resize(features.size());
        }
        for (int i = 0; i < ck_N; i++)
        {
            for (int j = 0; j < features.size(); j++)
            {
                res[i][j].resize(features[j].size());
            }//之后才能对三维数组设定大小，否则内存出错
        }        //定义每一类中不同的特征对应的样本个数
        vector<vector<vector<int>>> fenzi(ck_N);
        for(int n=0;n<ck_N;n++)
        {
            fenzi[n].resize(features.size());
        }
        for (int i = 0; i < ck_N; i++)
        {
            for (int j = 0; j < features.size(); j++)
            {
                fenzi[i][j].resize(features[j].size());
                for(int k =0 ;k<features[j].size();k++)
                {
                    fenzi[i][j][k]=0;
                }
            }//之后才能对三维数组设定大小，否则内存出错
        }        //计算分子和分母
        for(int i=0;i<ck_N;i++)
        {
            for(int j=0;j<N;j++)
            {
                if(Indication_function(data[j].labels,Ck[i]))
                {
                    fenmu[i]++;
                    //cout<<fenmu[i]<<endl;
                    for(int k=0;k<features.size();k++)
                    {
                        for(int l=0;l<features[k].size();l++)
                        {
                              if(Indication_function(data[j].samples[k],features[k][l]))
                                  fenzi[i][k][l]++;//分子不对应该也是三维的
                                  //cout<<fenzi[i][l]<<" "<<endl;
                        }
                    }                }
            }
        }
        //计算结果
        for(int i=0;i<ck_N;i++)
        {
            for(int j=0;j<features.size();j++)
            {
                for(int l=0;l<features[j].size();l++)
                {
                    res[i][j][l] = fenzi[i][j][l]/(double)fenmu[i];
                    //cout<<res[i][j][l]<<endl;
                }
            }
        }
        return res;
    }
    /**预测输入样本x的类别***/
    vector<double> Predict(vector<double> x,vector<int> Ck,vector<double> Priori_Probability,
                           vector<vector<vector<double>>> Conditional_Probability,vector<vector<double>> features)
    {
        int ck_N = Ck.size();
        vector<double> res;
        vector<double> temp;
        double temp1=1;        for(int i=0;i<ck_N;i++)
        {
           for(int j=0;j<Conditional_Probability[i].size();j++)//特征数量
           {
               for(int k=0;k<Conditional_Probability[i][j].size();k++)//每个特征的取值
               {
                   if(x[j] == features[j][k])
                   {
                       temp.push_back(Conditional_Probability[i][j][k]);
                       break;
                   }
               }
           }
           for(int l = 0;l<temp.size();l++)
           {
               temp1 = temp1*temp[l];
           }
           res.push_back(Priori_Probability[i]*temp1);
           temp1=1;
           temp.clear();
        }
        return res;
    }
    /**根据预测的概率，找到最大的值**/
    int Predict_class(vector<double> res,vector<int> Ck)
    {
        int n= res.size();
        double temp=res[0];
        int orth=0;
        for(int i=1;i<n;i++)
        {
            if(res[i]>temp)
            {
                temp = res[i];
                orth =i;
            }
        }
        return Ck[orth];
    }
};
int main()
{
    Bayes by;
    int N = by.loadData();
    cout<<"样本总数： "<< N <<endl;
    vector<int> C ;//Ck是类别的不同
    for(int i=0;i<N;i++)
    {
        C.push_back(data[i].labels);
    }
    vector<int> Ck = by.find_different(C);    vector<double> pp = by.Priori_Probability(Ck,data,N);
    cout<<"测试先验概率是否正确："<<endl;
    for (int j =0 ;j<pp.size();j++)
    {
        cout<<pp[j]<<endl;
    }    vector<vector<double>> Features = by.find_features(data,N);    cout<<"测试特征及特征取值是否正确："<<endl;
    for(int i=0;i<Features.size();i++)
    {
        for(int j=0;j<Features[i].size();j++)
            cout<<Features[i][j]<<" ";
        cout<<endl;
    }
    cout<<"测试条件概率是否正确："<<endl;    vector<vector<vector<double>>> res = by.Conditional_Probability(Ck,Features,data,N);
    for(int i=0;i<res.size();i++)
    {
        for(int j=0;j<res[i].size();j++)
        {
            for(int l=0;l<res[i][j].size();l++)
            {
                cout<< res[i][j][l]<<" ";
            }
            cout<<endl;
        }
    }    //预测样本的属性
    vector<double> x;
    x.push_back(2);
    x.push_back(9);
    vector<double> predict= by.Predict(x,Ck,pp,res,Features);
    cout<<"样本x预测为每一个类别的概率："<<endl;
    for(int i=0;i<predict.size();i++)
    {
        cout<<predict[i]<<endl;
    }    int pre_class = by.Predict_class(predict,Ck);
    cout<<"样本X的预测类别为："<<pre_class<<endl;
    return 0;
}