第一章 绪论

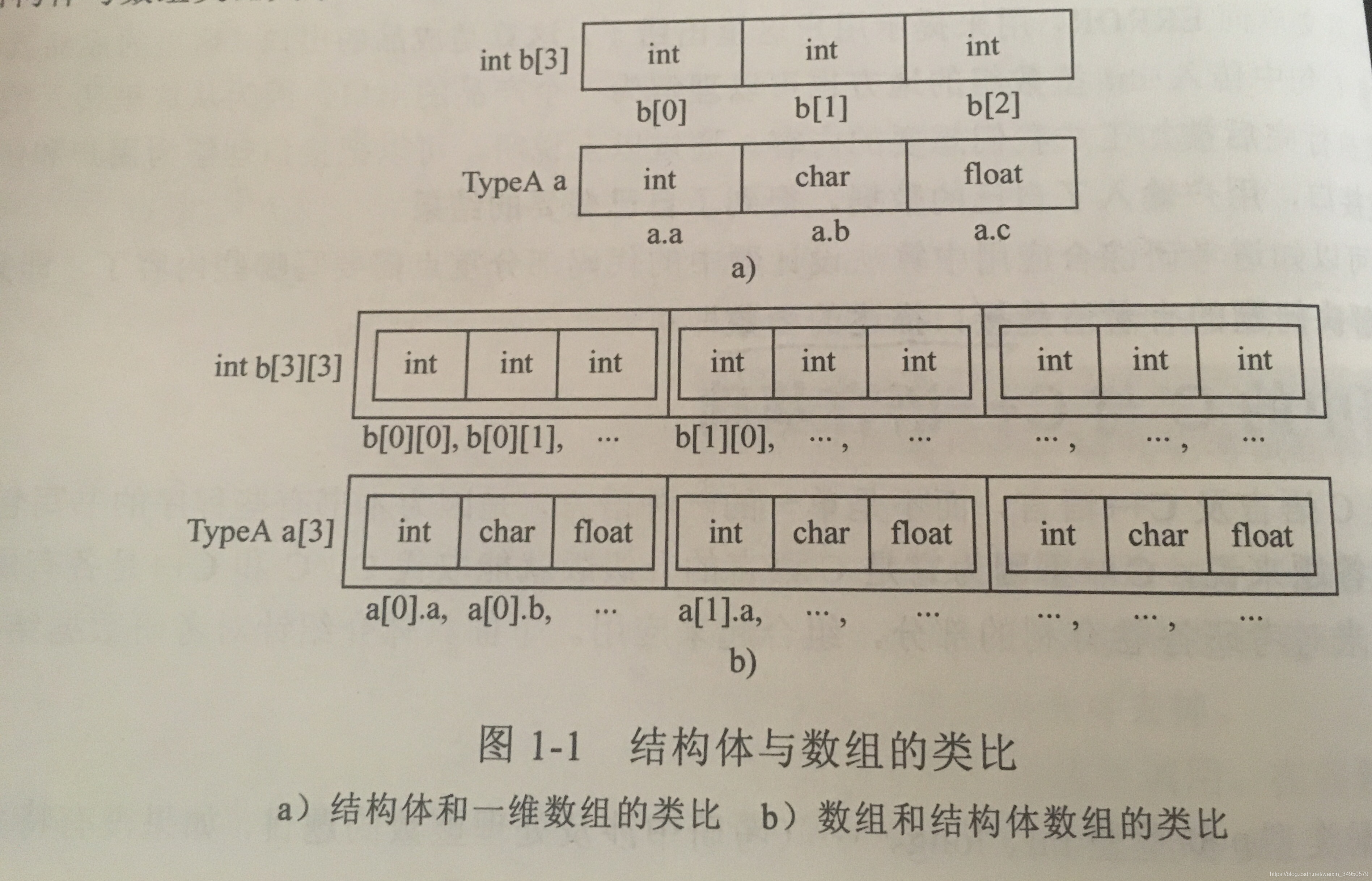
语言基础

（1）结构型

 int a[maxsize];

typedef struct
{
	int a;
	char b;
	float c;
}TypeA;

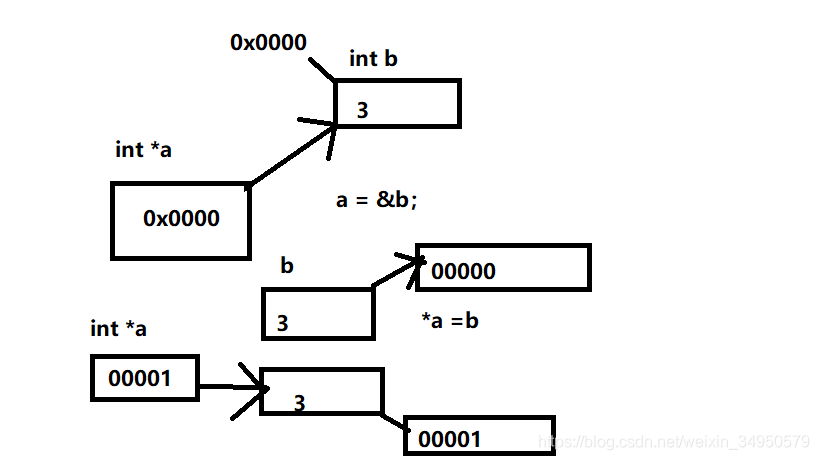
(2)指针型``

int *a;
char *b;
float *c;
TypeA *d;

如果a是个指针型变量，且它指向了一个变量b,则a中存放变量b所在的地址。*a就是取变量b的内容（x=*a等价于x=b） &b就是取变量b的地址 a=&b 就是大家所说的a指向b

• 对比
  a=&b a指向了b
  *a=b a指向空间的值改成了b的值
  
  （3）节点的构造
• 链表节点的定义

typedef strut Node
{
    int data;
    struct Node *next; // 指向node型变量指针
}Node;

（2） 二叉树节点的定义

typedef stuct BTNode
{
		int data；
		struct BTNode *lchild；
		struct BTNode *rchild；
}BTNode,*btnode;

BTNode *p 和 btnode p 等价
两种方法制作二叉树节点

① BTNode BT;
② BTNode *BT;
BT =(BTNode*) malloc(sizeof(BTNode));

第一种只制作了一个节点；
第二种定义节点变量指针BT，然后申请节点的内存空间，让BT指向这片内存空间，完成了节点制作。不然只是个指针，谁也没指。
第二种BT可以指向其他结点，而第一种不行。第一种BT就是某个节点的名字，一但定义好，不能脱离了
第一种赋值 x=BT.data 第二种 x=BT->data 或者(*BT).data

申请一组结点

int *p;
p =(int*) malloc(sizeof(n*int));

p指向数组中第一个元素的地址 取值和一般数组一样 比如取第二个p[1]

(4)
1)typedef 给现有数据类型起新名字

 typedef int wudi；

2)#define

#define maxsize 50；

2.函数

int a;
void f(int x)
{
   ++x;
}
//a=0;
//f(a)=0;


void f(int &x)
{
   ++x;
}
//f(a)=1


void f(int *&x)
{
   ++x;
}
//指针型变量需要改变的写法


void f(int x[],int n)
{
   ...;
}

void f(int x[][maxsize],int n)
{
   ...;
}

void f(int x[][5],int n)
{
   ...;
}
int a[10][5];
int b[10][3];
f(a);    //参数正确
f(b);	 //参数错误
//数组作为参数传入函数，函数就是对传入的数组本身进行操作，都是引用型

1.21 考研中的算法时间复杂度分析

O(1)≤O(㏒₂(n))≤O(n)≤O(n㏒₂(n))≤O(n²)≤O(n³)≤O(n^k) ≤ O(2 ⁿ)≤O(n!)≤O(n ⁿ)

• 将最坏情况作为算法时间复杂度的度量

void fun(int n)
{
 int i=1,j=100;
 while(i<n)
 {
  ++j;
  i+=2;
 }
 
}

第一步
1)找基本操作，一般取最深层循环内的语句所描述的操作作为基本操作
2）确定规模 由i<n可知，循环次数(基本操作执行的次数)和参数n有关，因此n就是我们的规模n
第二步
计算出f(n)
n确定以后，循环结束和i有关。i的初值为1，每次自增2，假设i自增m次后循环结束，则i最后的值为1+2m，因此有1+2m+K=n(其中K为一个常数)，，用k修正1+2m，m=(n-1-k)/2,可以发现其中增长最快的项为n/2,因此时间复杂度为 T(n)=O(n)

void fun(int n)
{
 int i,j,x=0;
 for(int i=0;i<n;++i)
 	for(int j=i+1;j<n;++j)
 		++x;
}

(n–1)+(n–2)+…+3+2+1
n(n-1)/2
T(n)=O(n²）

void fun(int n)
{
	int i=0,s=0;
	while(s<n)
	{
		++i;
		s=s+i;
	}
}

1.2.3 考研算法空间复杂度

---

1.3 数据结构算法基本概念

1. 数据：所有输入到计算机并被程序处理的符号总称
2. 数据元素：数据基本单位，若干数据项组成
3. 数据项：最基本，不可分割数据单位
4. 数据对象：性质相同数据元素集合
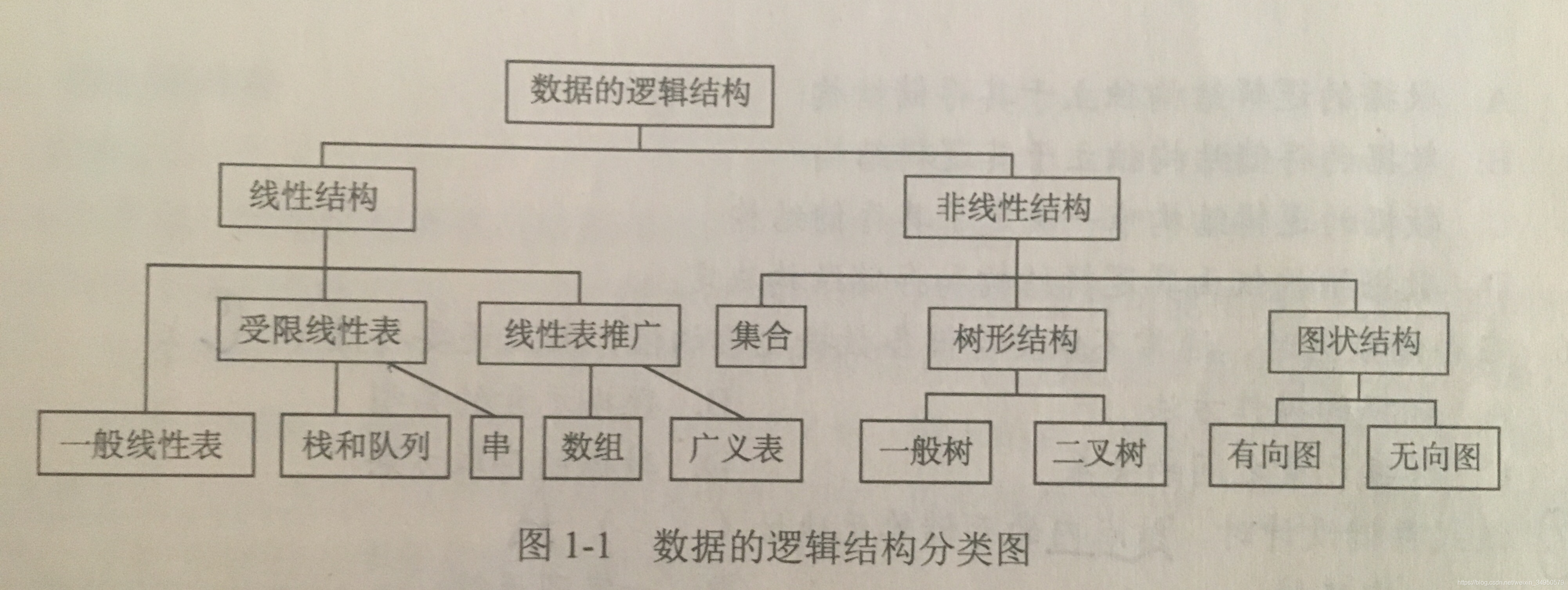
5. 数据结构：存在特定关系的数据元素集合。包括逻辑结构、存储结构、数据运算。
6. 数据逻辑结构：
   (1)线性结构
   1)唯一第一个元素
   2)唯一最后一个元素
   3)除最后一个，都以唯一后继
   4)除第一个，都以唯一前驱
   (2)非线性结构 ：一对多 树和图
7. 数据物理结构
   物理结构又称储存结构
   (1)顺序存储 : 随机存取 每个元素最少存储空间 一整块存储单元 产生较多的外部碎片
   (2)链式存储 无碎片 占用额外空间 顺序存取
   (3)索引存储 索引表 检索速度快 增删花费时间多
   (4)散列存储 速度快 散列函数不好会冲突 增加时间和空间开销
   

---

1.3.2 算法的概念

算法特性：有穷性、确定性(每一步有确定定义)、输入、输出、可行性
设计目标：正确性、可读性、健壮性(容错，对不合理数据检查)。高效率与低存储

---

习题

• 算法原地工作：额外空间是常数
• 属于逻辑结构（不是物理结构）：就是有多种物理存储方式
• 链式存储设计，结点内存储地址连续
• 长度m和n的升序链表，合并为长度m+n的降序链表，时间复杂度O(max(m,n))
• 如下函数mergesort()执行时间复杂度为多少？假设函数调用被写为mergesort(1,n),函数merge时间复杂度为O(n)

void mergesort(int i,int j)
{
	int m;
	if(i!=j)
	{
		m=(i+j)/2;
		mergesort(i,m);
		mergesort(m+1,j);
		merge(i,j,m);
	}
}

1.显然规模为n，基本操作是merge()，复杂度O(n)，merge内基本操作设为cn，函数mergesort()基本操作次数为f(n),则有
f(n)=2f(n/2)+cn;
=2²f(n/4)+2cn             2 x(2xf(n/4)+cn x 1/2)+cn
=2³f(n/8)+3cn            (2²) x(2xf(n/8)+cn x 1/4)+2cn
=2^kf(n/2^k)+kcn
由函数 mergesort()可知 f(1)=c x 1=c;
由n=2^k -> (k=log₂n) 带入最后一式 f(n)=nc+log₂ncn
f(n)=cn+cnlog₂n



1.一个算法所需时间由下述递归方程表示，试求出该算法的时间复杂度的级别。
T(n)=      1                 若n=1
          2T(n/2)+n        若n>1



求解斐波那契数列递归和非递归
F(n)   = 1                      n=0,1
           F(n-1)+F(n-2)       n>1
.递归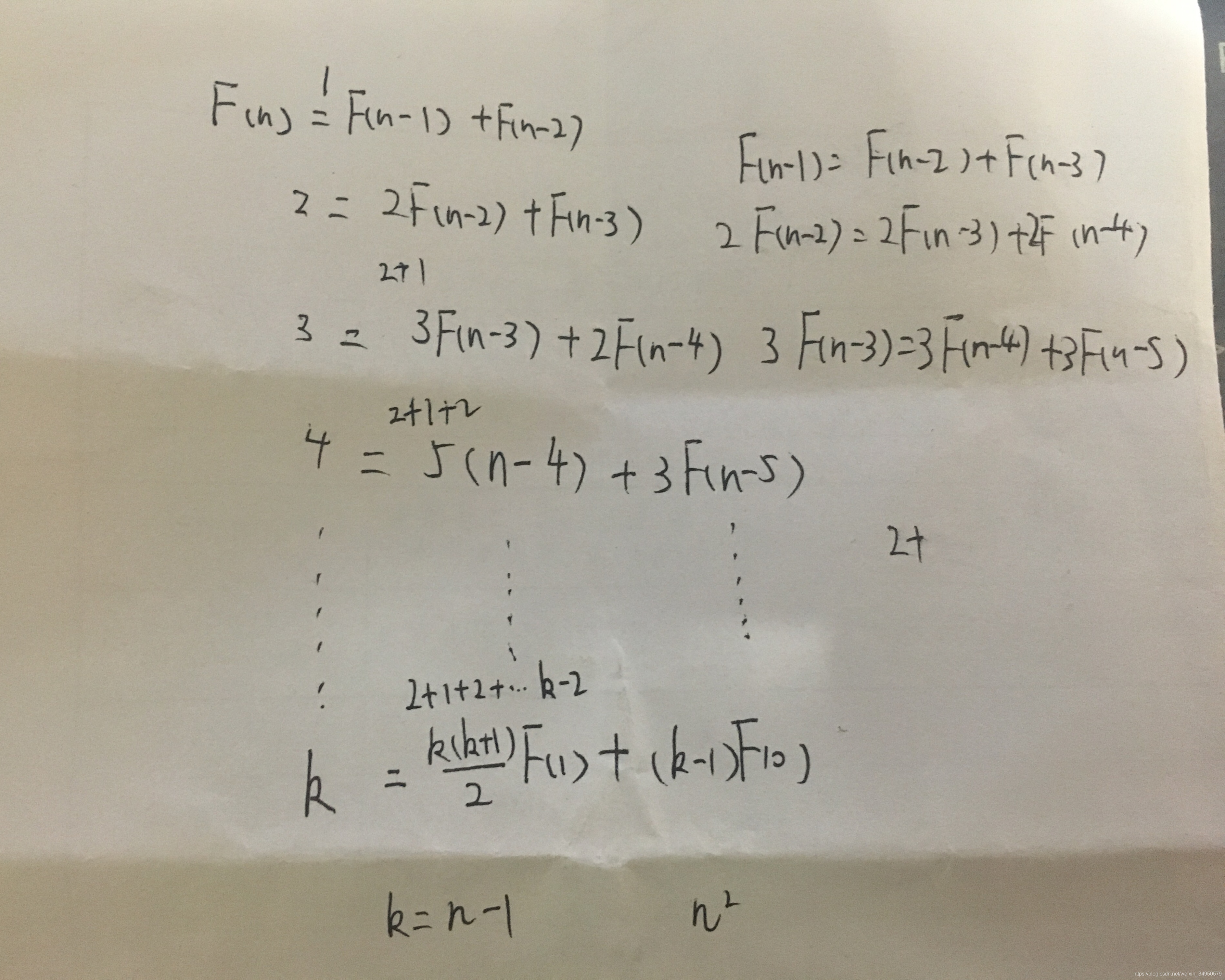
非递归

#include<iostream>
using namespace std;

long Fibonacci(int n) {
    if (n <= 2)
        return 1;
    else {
        long num1 = 1;
        long num2 = 1;
        for (int i = 2;i < n - 1;i++) {
            num2 = num1 + num2;
            num1 = num2 - num1;
        }
        return num1 + num2;
    }
}

int main() {
    cout << "Enter an integer number:" << endl;
    int N;
    cin >> N;
    cout << Fibonacci(N) << endl;
    system("pause");
    return 0;
}

从n(>2)开始计算，用F(n-1)和F(n-2)两个数相加求出结果，这样就避免了大量的重复计算，它的效率比递归算法快得多，算法的时间复杂度与n成正比，即算法的时间复杂度为O(n)