2.1 线性表的基本概念与实现
1.定义:相同特性数据元素的有限序列。长度n>=0
2.顺序表链表比较:顺序表,随机访问,连续空间,存储分配预先进行。插入移动元素。
插入删除平均时间复杂度O(n)
链表:顺序访问,空间利用率低,存储空间动态分配。插入不需要移动元素。
循环单链表:
带头结点,head=head->next 链表为空
不带头结点,head等于null链表为空
循环双链表:
不带头结点,head为null
带头结点,head->next == head;
head->prior ==head;
静态链表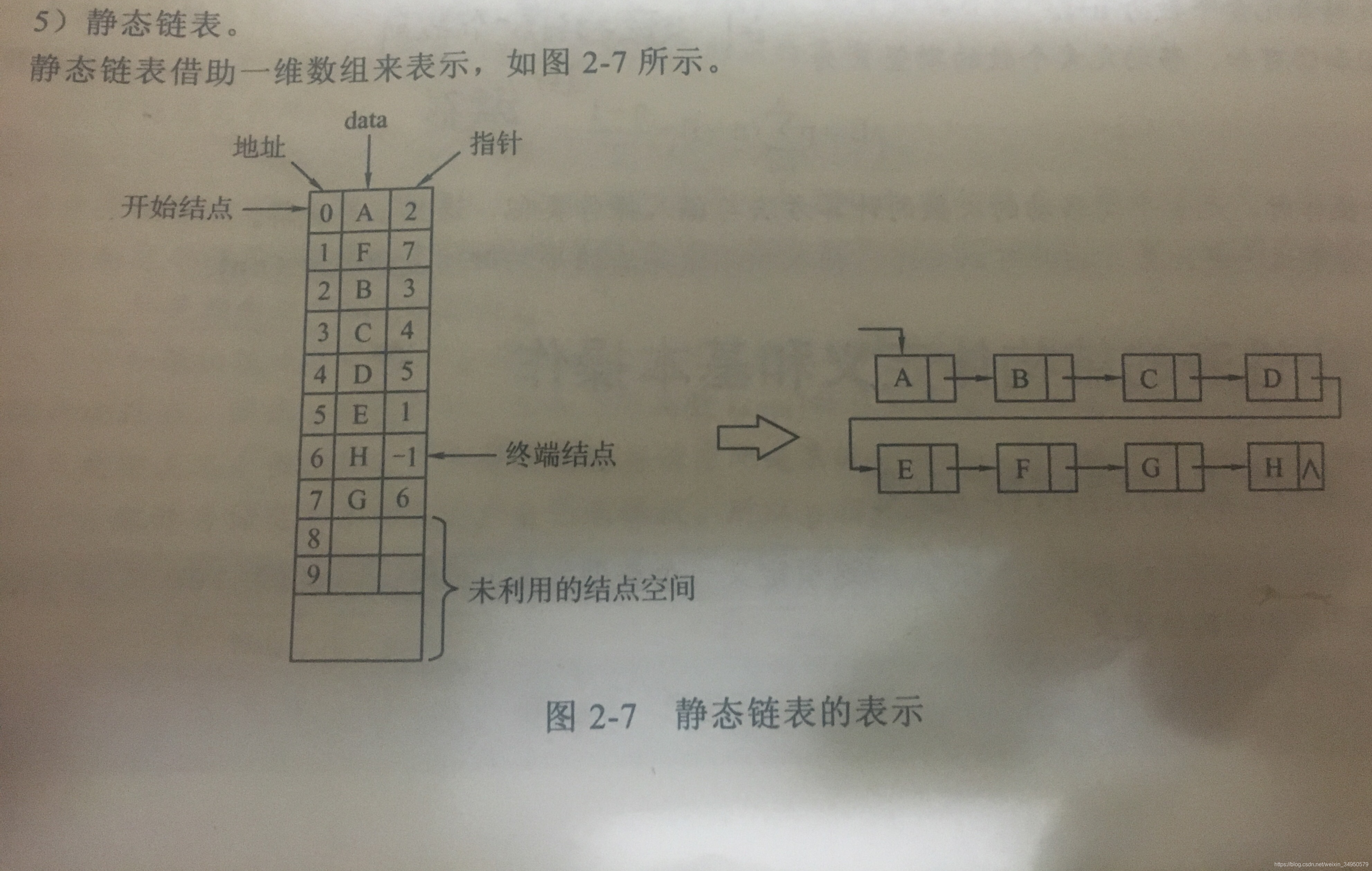
静态链表结构体数组。
2.2 线性表的结构体定义和操作
2.2.1线性表的结构体定义
1.顺序表结构体定义
typedef struct
{
int data[maxsize];
int length;
}Sqlist;
//简写
int A[maxsize];
int n;
2.单链表节点定义
typedef struct LNode
{
int data;
struct LNode *next;
}LNode;
3.双链表节点定义
typedef struct DLNode
{
int data;
struct DLNode *prior;
struct DLNode *next;
}DLNode;
2.2.2 顺序表的操作
- 已知一个顺序表L,元素递增有序,插入x,仍然递增有序
int findElem(Sqlist L,int x)
{
int i;//i为顺序表数组下标
for(int i=0;i<L.length;++i){
if(x < L.data[i])
{
return i;
}
}
return i; //若不存在比x还大的数,i=L.length
}
void insertElem(Sqlist &L,int x)
{
int p,i;
p=findElem(L,x);
for(i=L.length-1;i>=p;--i;)
L.data[i+1] = L.data[i];
L.data[p] = x;
++(L.length);
}
基本操作
(1)按元素值查找算法
int findElem(Sqlist L,int e)
{
int i;
for(int i=0;i<L.length;++i){
if(e = L.data[i])
{
return i;
}
}
return -1; //没找到
}
(2)插入元素的方法
顺序表L的第p(0到length)个位置插入心元素e
void insertElem(Sqlist &L,int p,int e)
{
int i;
if(p<0 || p>L.length|| L.length=maxSize)
return 0;
for(i=L.length-1;i>=p;--i;)
L.data[i+1] = L.data[i];
L.data[p] = e;
++(L.length);
return 1;
}
- 例2-2 删除顺序表L中下标为p(0<=p<=length-1)的元素,成功返回1,否则返回0,并将被删除元素的值赋给e。
int deleteElem(Sqlist &L,int p,int & e)
{
int i;
if(p<0||p>L.length-1)
return 0;
e=L.data[p];
for(i=p;i<L.length-1;++i)
L.data[i]=L.data[i+1];
--(L.length);
return 1;
}
基本操作
- 初始化顺序表的算法
void initList(Sqlist &L)
{
L.length=0;
}
























 590
590

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








