基本原理
先将原问题表达为 f(x)=0 求零根问题
设 r 是 f(x)=0 的一个根,则 x0 处的切线方程为 ![]()
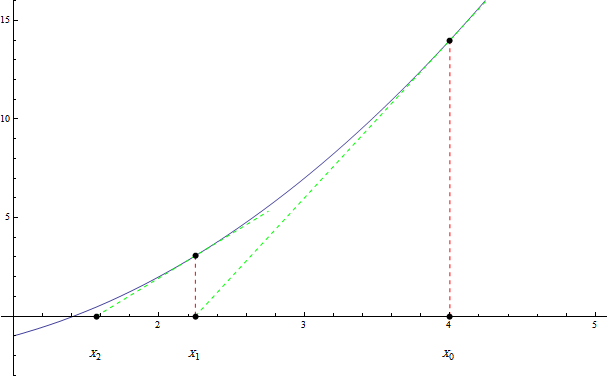
选取 x0 为接近根的初始值,不断用过 ![]() 点的切线将
点的切线将 ![]() 的过程就是迭代过程。
的过程就是迭代过程。
所以 xn 是 ![]() 的解。
的解。
整理并解得:
![]()
即为迭代通式。
迭代的适用性
首先原函数的导数可以比较容易的可得,且其导函数中不含有形如原函数的因子。
另外需要关注两个问题:
迭代是否收敛? 直接决定是否可以使用迭代法
迭代的收敛速度? 决定了逼近的速度
牛顿迭代法具有较高的收敛速度,收敛阶数为=2。
而牛顿迭代法的局部收敛性较强,只有初值充分地接近,才能确保迭代序列的收敛性。
为了放宽对局部收敛性的限制,必须再增加条件建立以下收敛的充分条件。
对于f(x)在区间[a,b]上,需满足:
f(a)f(b)<0,即保证根的存在性
f'(x)≠0,单调性是一致的,即有唯一的解
f"(x) 不变号,即函数的凹向不变
f'(x0)f"(x0)>0
因此,在放宽x0取值时,必须要满足上述4个条件才可以迭代逼近。
求 的迭代式
的迭代式
该问题等价于![]() 的问题。
的问题。
所以有 f'(x)=2x ,代入到迭代通式中得:
![]()
简化整理得:
![]()
即为![]() 的逼近法解决的迭代式。
的逼近法解决的迭代式。
求 的迭代式
的迭代式
该问题等价于![]() 。
。
所以有 f'(x)=3x2 ,代入到迭代通式中得:
![]()
简化整理得:
![]()
即为![]() 的逼近法解决的迭代式。
的逼近法解决的迭代式。
实际应用
讨论牛顿逼近法一方面可以了解Math.sqrt()实现,另一方面,对于大数计算/高精度计算就显得非常重要了。
例如Java中BigDecimal对象没有sqrt方法,如果需要对一个大数(或者一个高精度实数)进行开方应该怎么办?
就按照上面的方法我们自己实现一个:(关键点就是得到迭代式)
// 利用BigDecimal做数值容器
// 利用上面求出的牛顿法迭代式
// 实现 对任意大数/任意精度实数进行开方
static BigDecimal newtonMethodSqrt2 (BigDecimal a, int precision) {
BigDecimal _2 = new BigDecimal(2);
BigDecimal xn = a.divide(_2); // x0的初始值
MathContext mc = new MathContext(precision, RoundingMode.HALF_UP);
int loop = (int) Math.ceil(Math.log(precision) / Math.log(2));
for (int i = loop; i >= 0; i--) {
xn = xn.add(a.divide(xn, mc)).divide(_2, mc); // 上面求出的迭代式
}
return xn;
}
public static void main(String[] args) {
System.out.println(newtonMethodSqrt2(new BigDecimal(2), 100));
}这就是对一个大数/高精度数进行开方的运算(指定了100位精度),看一下运算结果,再对比一下高精度计算器bc的结果:
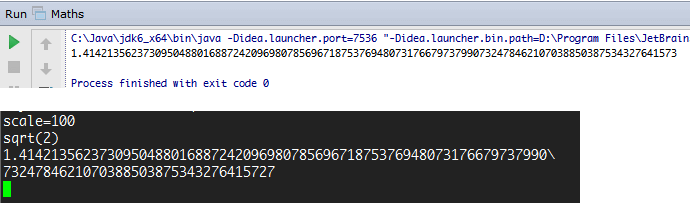
与bc结果一致,即有了![]() 的精度。
的精度。
特别注意到,当上面循环改为 i>0 时,第97位以后出现偏差,即有了![]() 的精度。
的精度。
这也说明了,有限精度多次计算造成精度降低,于是,要适当的提高精度要求或者增加迭代次数。
其它
某些高阶方程问题无法用计算机直接计算的时候,可以尝试使用牛顿迭代法。
显然,要利用计算机解决这些问题,就需要算出迭代式,这才是程序的关键。
前面已经给出了利用牛顿迭代法求开方的例子。同时也给出开三次方的迭代式,上面的newtonMethodSqrt2按通式稍稍变形即可计算开三次方。
同理,用通式算出开n次方的迭代式,也可以计算。
同理,对于大数 loga(x) 的计算,等价于对 X 开 a 次方的问题,所以如法炮制。
还有,对于其它某些高阶问题需要用迭代法解决时,发现其导数不易求得或者牛顿法迭代式比原式更复杂,则可以考虑使用牛顿迭代法的变种,比如牛顿下山法、单点弦截法、双点弦截法等来解决,但通常它们具有更低的收敛速度,即需要更多次的迭代才能很好的逼近真实值。





















 2373
2373

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








