[临时]单源最短路径（Dijkstra算法）-优快云博客

本文详细介绍迪杰斯特拉算法的实现原理及过程，并通过具体示例代码展示如何使用该算法来解决带权有向图中的最短路径问题。文章包括算法流程、参数解释、模板代码及运行结果。

　　因为没有原创内容，相当于看书笔记，因此本打算发在QQZone，但因为QQ空间日志忽然服务器繁忙，大骂腾讯无奈还是把此日志临时发布在自己的博客上。

　　参考资料：《计算机算法设计与分析》（第三版）。
　　条件：
　　（1）带权有向图 G = (V, E); 任意边的权 >= 0;

　　算法：
　　贪心法。体现在从源节点开始，每次从集合S外“选一个最近的节点”添加到S中，然后对dist数组做更新。

　　参数说明：

　　T：模板参数，权值类型。（计量长度的数据类型）

　　int n; 图的节点数；　　

　　int v; 出发节点（源节点）的索引。

　　T dist[]; dist[i]表示当前条件下 v 到 i 节点之间的最短距离。求解过程中这个数组随着集合S的扩充而动态变化。

　　int prev[]; prev[i]表示从 v 到 i 节点之间的最短距离路径上的前一个节点。可以通过这个数组反塑获取到完整路径。

　　T *c; 图的矩阵表示。c[i][j]表示边（i，j）的权。当无通路时为一个大数。

=========================　　

　　　　　　代码：

=========================

Code_Dijkstra
// Dijkstra.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include <stdlib.h>
#include <stdio.h>

#define maxint 0x7fffffff

//dijkstra 算法，索引是从1开始的

template <class T>
void Dijkstra(int n, int v, T dist[], int prev[], T* c)
{
    int i, j, temp, u;
    T newdist;
    //bool s[6];
    bool *s = (bool*)malloc(n*sizeof(bool));
    printf("sizeof(bool) = %d bytes. \n", sizeof(bool)); //1 bytes;

    //[0] 初始化
    for(i = 0; i < n; i++)
    {
        dist[i] = c[v*n+i]; //c[v][i]
        s[i]=false;            //在集合S外
        if(dist[i] == maxint) prev[i] = 0;
        else prev[i] = v;
    }

    //把节点v放入集合S中
    dist[v]=0;
    s[v] = true;

    //向S集合中依次添加其他（n-1）个节点
    for(i = 0; i < (n-1); i++)
    {
        temp = maxint;
        u = v;

        //[1] 选出S集合外的距离最近的一个点u
        for(j = 0; j < n; j++)
        {
            if(!s[j] && (dist[j] < temp))
            {
                u = j;
                temp = dist[j];
            }
        }

        //[2] 把u放入S集合；
        s[u] = true;

        //[3] 调整dist数组和prev数组
        for(j = 0; j < n; j++)
        {
            //查看 u 到 j 节点之间有通路？？？
            if( !s[j] && c[u*n+j] < maxint ) //if( !s[j] && c[u][j] < maxint )
            {
                newdist = dist[u] + c[u*n+j]; //newdist = dist[u]+ c[u][j];
                if(newdist < dist[j])
                {
                    dist[j] = newdist;
                    prev[j] =u;
                }
            }
        }
    }

    free(s);
}

int main(int argc, char* argv[])
{
    int i, dist[5], prev[5];
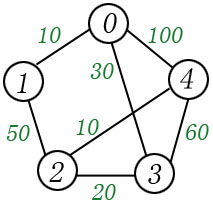
    int c[5][5] =
    {
        //     0       1       2       3       4
        {      0,     10, maxint,     30,    100 }, //0
        {     10,      0,     50, maxint, maxint }, //1
        { maxint,     50,      0,     20,     10 }, //2
        {     30, maxint,     20,      0,     60 }, //3
        {    100, maxint,     10,     60,      0 }  //4
    };

    //调用算法节点数=5，出发节点=0
    Dijkstra<int>(5, 0, dist, prev, (int*)c);

    //【1】打印节点1到其他节点的最短距离
    printf("dist: ");
    for(i=0; i<5; i++)    printf("%d,", dist[i]);
    printf("\n");

    //【2】打印prev数组，记录从出发点到本节点的最短路径的上一个节点
    printf("prev: ");
    for(i=0; i<5; i++) printf("%d,", prev[i]);
    printf("\n");

    //【3】打印从0到4的最短路径
    printf("0->4 Path: ");
    int stack[5], top=-1;
    stack[++top] = 4;
    //逆向追溯节点（入栈）
    while(true)
    {
        stack[top+1] = prev[stack[top]];
        top++;

        //栈顶是否已经是出发点
        if(stack[top] == 0)
            break;
    }
    //节点依次出栈
    for(;top>0;top--)
        printf("%d - ", stack[top]);
    //栈中最后一个节点
    printf("%d\n", stack[top]);
    return 0;
}