蓝桥杯 排列数字-今有7对数字

今有7对数字：两个1，两个2，两个3，...两个7，把它们排成一行。
要求，两个1间有1个其它数字，两个2间有2个其它数字，以此类推，两个7之间有7个其它数字。如下就是一个符合要求的排列：

17126425374635

当然，如果把它倒过来，也是符合要求的。

请你找出另一种符合要求的排列法，并且这个排列法是以74开头的。

回溯虐我很多遍啊。。。

我的递归和回溯真的不行啊，唉，还好调试许久终于搞定了；

ans：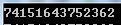

 1 #include<iostream>
 2 #include<algorithm>
 3 #include<cstdio>
 4 #include<cstring>
 5 #include<queue>
 6 #include<string>
 7 #include<cmath>
 8 using namespace std;
 9 int a[20];
10 int cou[20],b[20];
11 void dfs(int i,int t,int p)//  t 表示的是多少位；
12 {
13 
14       if(p==10)
15       {
16           //cout<<"whywhy"<<endl;
17           for(int mm =1; mm<=14; mm++)
18                printf("%d",a[mm]);
19                     printf("\n");
20                     return ;
21       }
22     if(cou[i]==2 || a[t]!=0 || a[t+i+1]!=0|| i+t>13)
23     {
24         //cout<<"i= "<<i<<"t= "<<t<<endl;
25         //cout<<cou[i]<<" "<<a[t]<<" "<<a[t+i+1]<<endl;
26         //cout<<"what what"<<endl;
27         return ;
28     }
29       else
30       {
31         a[t]=i;
32         a[t+i+1]=i;
33         cou[i]=2;
34         for(int k=1;k<=7;k++)
35         {
36           for(int j =t+1;j<=14;j++)
37           {
38              dfs(k,j,p+2);
39           }
40         }
41         a[t]=0;
42         a[t+i+1]=0;
43         cou[i]=0;
44 
45      }
46 }
47 int main()
48 {
49     memset(a,0,sizeof(a));
50     memset(cou,0,sizeof(cou));//统计出现的次数
51     a[1] = 7;
52     a[2] = 4;
53     a[7] = 4;
54     a[9] = 7;
55     cou[7] = 2;
56     cou[4] = 2;
57     dfs(1,3,0);
58     return 0;
59 }

 

转载于:https://www.cnblogs.com/lovychen/p/4411288.html