优势比(Odds Ratios)

最新推荐文章于 2025-04-09 09:30:20 发布
最新推荐文章于 2025-04-09 09:30:20 发布
阅读量1.5w 收藏 19
点赞数 3
文章标签： python 数据结构与算法 r语言
原文链接：https://my.oschina.net/u/1785519/blog/1573091
版权

2019独角兽企业重金招聘Python工程师标准>>> hot3.png


优势比反映了从 发生比来看， 一个特定事件在一个组发生的可能性对于另一个组发生的可能性大小

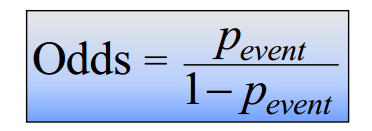
14015552_h7LR.png
    
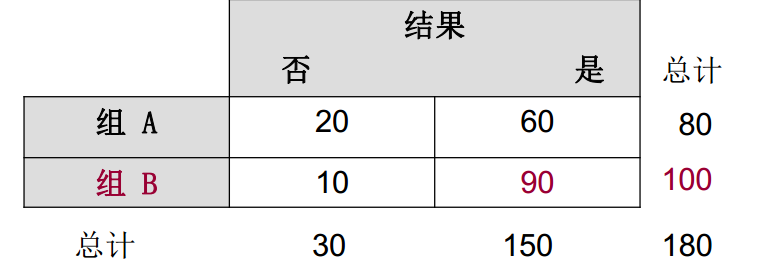
14015552_OFol.png

 结果概率：B组中结果为“是”的总计 / B组结果总计 = B组中“是”的概率 = 90/100 = 0.9

 发生比：两个结果概率的比
 B组中“是”的概率 0.9 / B组中“否”的概率 0.10 ==> B组中‘是’的发生比 = 0.9/0.10 =9
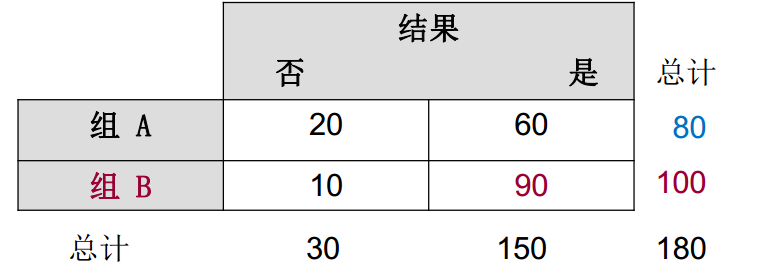
14015552_wlhG.png
 优势比：两个发生比相比
 B组中‘是’的发生比 = 9 / A组中‘是’的发生比 =3 ==> Odds Ratio，B 对 A = 9/3=3
 

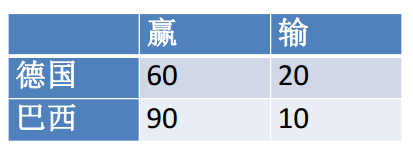
14015552_i9Np.png
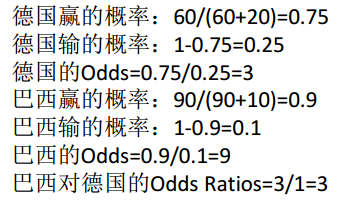
14015553_qOwO.png
14015553_YEK1.png












转载于:https://my.oschina.net/u/1785519/blog/1573091

R语言使用epiDisplay包的cc函数计算优势比（Odds Ratio，OR）及其置信区间、包含列联表的独立性检验和Fisher精确概率检验、可视化优势比（Odds Ratio，OR）的变化图
statistics+insight+vista+power
06-03 557
R语言使用epiDisplay包的cc函数计算优势比（Odds Ratio，OR）及其置信区间、包含列联表的独立性检验和Fisher精确概率检验、可视化优势比（Odds Ratio，OR）的变化图
R语言使用epiDisplay包的cc函数计算优势比（Odds Ratio，OR）的值及其置信区间并可视化（包含卡方检验和Fisher精确检验结果）
statistics+insight+vista+power
10-04 495
R语言使用epiDisplay包的cc函数计算优势比（Odds Ratio，OR）的值及其置信区间并可视化（包含卡方检验和Fisher精确检验结果）
【SAS】优比 Odds Ratio
大头山猪的窝
03-26 7175
目录请看下面[↓_↓]Odds Ratio 基本概念数学表达式Confidence interval 基本概念数学表达式Odds Ratio SAS绘图编程代码文章来源 Odds Ratio 基本概念 Odds Ratio 简称OR 中文 优比 某事件发生概率比上某事件不发生的概率 OR>1则发生该事件可能性高 OR<1则不发生该事件可能性高 数学表达式 吃药 没吃药 ...
OR（odd ratios）
likelet的专栏
03-20 1万+
OR值的全称是odd ratio, OR值是相对危险度，又称比值比，对于发病率很低的疾病来说，它是OR值即是相对危险度的精确估计值。 计算公式如下： Odd ratio, 95% CI 假定我们要鉴别一个基因（或者标记位点SNP）有两个等位基因（等位）:记为 Allele 1 Allele 2 Allele 1
【漫话机器学习系列】191.比值比（Odds Ratio，简称OR）
IT古董
04-09 737
比值比（Odds Ratio，简称OR）是统计学和医学研究中非常常见的一个指标，常用于比较两个不同组的事件发生的可能性。简单来说，比值比就是两个“比值（Odds）”之间的比。
优势比和最大似然
Alsace的专栏
01-25 2133
1. 优势比 odds ratio1.1 什么是优势比优势比(odds ratio；OR)是一种描述概率的方式，用于反映分类变量之间的相关性。优势：设定p为事件发生的概率，则发生的优势为，odds= p/1-p。优势比：p1为事件1发生的概率，p2为事件2发生的可能/概率，优势比为odds ratio= (p1/(1-p1)) /(p2/(1-p2))可以理解为事件1发生的概率相较于事件2发生概率的比值。
python绘制优势率
GIS骆驼的GIS博客
04-24 2389
优势率是一个事件发生和不发生的概率之间的比率，公式为odds=q/(1-q)，q为一个事件发生的 概率。 为了更直观的看到这个公式的样子，所以用python绘制了公式曲线，q间隔取为0.01. python代码如下： import matplotlib.pyplot as plt from pylab import figure,show,np t = np.arange(0.0, 1.0, 0.01) j=t/(1-t) fig = figure() ax1 = fig.add_subplot(21
【深度学习基础知识 - 43】优势比的概念
yanyuxiangtoday的博客
08-31 2886
优势比 假设在m个独立自变量，x1、x2…xm的作用下，记事件y取1的概率为： 则事件y取0的概率为p = 1 - p，则取1和取0的概率之比为： 上式就称为事件的优势比。 博主会持续更新一些深度学习相关的基础知识以及工作中遇到的问题和感悟，喜欢请关注、点赞、收藏。 ...
【数学建模】统计领域的逻辑回归（分类变量相关性检验、优势比OR、包含分类变量的多元逻辑回归）
lys_828的博客
04-03 2416
统计领域的逻辑回归0 指导方针1 分类变量之间的相关性检验1.1 分类变量相关性的示例1.2 列联表分析1.3 信用风险建模案例1.3.1 制作两分类变量交叉表并求解交叉频率1.3.2 相关性判定1.3.3 p值与𝛼 显著性水平1.3.4 卡方检验1.4 优势比（Odds Ratios）2 一元连续变量逻辑回归2.1 逻辑回归模型由来2.2 衍生变量生成2.3 数据采样与划分2.4 模型创建2.5 模型预测3 模型表现优劣的评估3.1 一致对于非一致对3.2 ROC曲线与AUC面积3.3 阈值调整与评估指标
可视化优势比的变化图（使用R语言）
HackDyno的博客
08-27 281
可视化优势比的变化图（使用R语言）在数据分析和可视化中，比较不同组别或条件之间的优势比（odds ratio）变化是一项常见的任务。R语言提供了丰富的工具和包，可以帮助我们实现这一目标。在本文中，我们将介绍如何使用R语言创建可视化优势比的变化图。首先，我们需要准备数据。假设我们有一个数据集包含两个类别的观察值，我们想要比较它们之间的优势比在不同条件下的变化。为了演示，我们可以生成一些虚拟数据。 接下来，我们将使用包计算不同条件下的优势比。我们可以使用函数将数据按条件分组，然后使用函数计算每个组别的优势比。这
医咖会免费STATA教程学习笔记——Odds Ratio（优势比值）的计算
Una20200519的博客
01-13 3116
准备工作： 导入数据库：webuse ccxmpl, clear 查看数据分布：list 1.方法一 请依次点击： 统计——流行病学及相关——流行病学家专用表——病例对照优势比——在“病例变量”中选择“case”，在“暴露变量”中输入“exp”——切换到“权重”选项卡——在“权重类型”下点选“频率权重”，并在“频率权重”下选择“pop”——确定 或者 在命令窗口输入：cc case exp [fweight = pop] 2.方法二 请依次点击： 统计——流行病学及相关——流行病学家专用表——病例对照优势比
R语言怎么计算优势比
weixin_35756373的博客
01-08 605
在R语言中，可以使用prop.test()函数来计算优势比。 例如，假设你有两个分组，分别为A和B，并且想要比较这两组之间的成功率(例如，给定一组试验数据，A组有30个成功的试验，共进行了100个试验，B组有40个成功的试验，共进行了200个试验)。 你可以这样计算优势比： # 首先计算两组的成功率 success_rate_A <- 30/100 success_rate_B <- ...
生物信息_odds_ratios、Likelihood_Ratios、发病率、frequency
BBka要黑化！
05-02 1321
case control risk-> G a c   T b d   odds ratio=(a/b)/(c/d) Likelihood ratio=(a/(a+b))/(c/(c+d)) Likelihood ratio也就是LR，LR越大，case与contr
odd ratio值在关联分析中的含义
庐州月光的博客
09-27 6405
欢迎关注”生信修炼手册”!在GWAS分析中，利用卡方检验，费舍尔精确检等方法，通过判断p值是否显著，我们可以分析snp位点与疾病之间是否存在关联，然而这得到的仅仅是一个定性的结论，如果存...
数据挖掘关于发生比
qq_40820323的博客
06-25 830
7.该问题与发生比有关： a)平均来说，违约信用卡贷款发生比为0.37的人群中违约的比例是多少？b)假设某人有16%的信用卡贷款违约概率， 则其违约的发生比是多少？...
机器学习基础：概率，发生比与Logit
youyanyu3817的博客
05-22 2868
机器学习基础：概率，发生比与Logit 概率是机器学习中最常见的概念，在分类算法(Classification)中经常出现，而Logit也是逻辑回归（Logistic Regression）中的重要概念，本文将总结概率（Probability），发生比（Odds）和Logit（log(odds)）之间的关系。 1. 概率，发生比与Logit的定义 1.1. 概率 概率是指一个事件发生的可能性，假设一个袋子里有若干红球和蓝球，用P来表示概率，则： P（抽到红球）=红球个数所有球个数\vphantom{}\\P
预测算法模型系列（六）
perliu的专栏
09-22 421
这个目前正在研究，等研究明白了，再来补充。
OR值的意义和计算公式，和95% CI
热门推荐
lj695242104的专栏
11-11 9万+
OR值的全称是oddratio,又称比值比，对于发病率很低的疾病来说，它是OR值即是相对危险度的精确估计值。 计算公式如下： Odd ratio, 95%CI 假定我们要鉴别一个基因（或者标记位点SNP）有两个等位基因（等位）:记为 Allele 1 Allele 2         Allele1 Al
有序逻辑回归cOR cOR指的是什么 列出参考依据
最新发布
05-10
### 有序逻辑回归中的 cOR 定义 在统计学中，有序逻辑回归（Ordinal Logistic Regression）用于建模具有自然顺序的分类因变量。累积优势比（Cumulative Odds Ratio, 简称 cOR）是一个重要的概念[^4]。它衡量的是某一类别及其以上类别的概率相对于较低类别的比例变化。 具体来说，在有序逻辑回归模型中，假设存在 \( k \) 类别，则第 \( j \) 类别及以上的累积概率可以表示为： \[ P(Y \geq j | X) = \frac{\exp(\beta_0 + \beta_1 X)}{1 + \exp(\beta_0 + \beta_1 X)} \] 其中 \( Y \) 是响应变量，\( X \) 是预测变量，而 \( \beta_0 \) 和 \( \beta_1 \) 则是待估参数。累积优势比 (cOR) 表示当自变量增加一个单位时，累积事件发生的几率的变化倍数[^5]。 如果某个解释变量 \( X_i \) 的系数为 \( b_i \)，那么对应的累计优势比如下计算得出： \[ cOR(X_i) = e^{b_i} \] 这意味着每增加一单位该变量，发生较高水平结果的概率会变为原来的 \( e^{b_i} \) 倍[^6]。 ### 实现代码示例 以下是基于 Python 使用 `statsmodels` 库来拟合有序逻辑回归并提取 cOR 的简单例子： ```python import statsmodels.api as sm from statsmodels.miscmodels.ordinal_model import OrderedModel # 数据准备省略... data['const'] = 1 # 添加截距项 model = OrderedModel(data['dependent_variable'], data[['independent_var', 'const']], distr='logit') result = model.fit(method='bfgs') print(result.summary()) # 提取系数并转换成 cOR coefficients = result.params cumulative_odds_ratios = np.exp(coefficients) print(cumulative_odds_ratios) ``` 此脚本展示了如何构建模型以及怎样从估计出来的参数得到相应的累积优势比数值。 ###
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值