机器学习（一） 贝叶斯法则与概念学习

　　贝叶斯学习算法应用于机器学习的有两个原因，第一：贝叶斯学习能够计算显式的假设概率，如

朴素贝叶斯分类器。第二：贝叶斯方法为理解机器学习的其他方法提供了手段，如分析FIND-S算法。

　　贝叶斯法则对与贝叶斯学习至关重要，其形式如下：

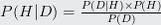
　　贝叶斯法则提供了一种计算假设概率的方法，它基于假设的先验概率、给定假设下观察到不同数据

的概率以及观察到的数据本身。其中P（H）用来代表在没有训练数据前假设H拥有的初始概率，因此其

通常被称为先验概率（prior probability），它反映了我们所拥有的关于假设H是一正确假设的机会的背景

知识。如果没有这一先验知识，那么我们可以简单地将每一候选假设赋予相同的先验假设。类似地，P（D）

代表了将要观察的训练数据D的先验概率。而P（D|H）就代表了假设H成立的情形下观测到数据D的概率。

但在机器学习中我们感兴趣的是P（H|D），即给出训练数据后假设H成立的概率。P（H|D）也被称为H的

后验概率，因为它反映了看到训练数据D后H成立的置信度。

　　而在许多学习场景中，学习器考虑候选假设集合H并在其中寻找给定数据D时可能性最大的假设H。这样

的具有最大可能性的假设被称为极大后验（maximum a posteriori, MAP）假设。确定MAP假设的方法是用

贝叶斯公式计算每个候选假设的后验概率。

　　

转载于:https://www.cnblogs.com/lxgeek/archive/2011/10/26/2224914.html