上一篇说的仿58同城loadingview的项目。中有一个利用贝塞尔曲线进行绘制圆的步骤,这个贝塞尔曲线理论挺复杂,特此单独说一下所知的和能用到的。
比方上一个loadingView的项目中。要用到Path.cubic()来使用贝塞尔曲线画一个圆,那么首先要了解的是
Path.cubic()方法的定义:
void cubicTo(float x1,float y1,float x2,float y2,float x3,float y3)
Add a cubic bezier from the last point,approaching control points(x1,y1)and(x2,y2),and ending at (x3,y3)什么意思呢。就是从我们的最后一个点出发以接近(x1,y1)(x2,y2)这两个点的方向走最后结束在(x3,y3)点。
什么叫接近呢?比方y = 1/x^3 这个函数的轨迹当x趋近于0时。轨迹无限趋近于Y轴值趋于无限大。
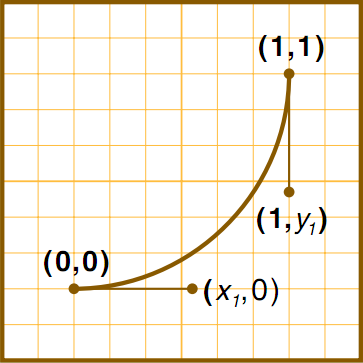
当曲线从0点出发以趋近1点的方向前进终结于4点时就会呈现这样一个轨迹。
所以当想以三次方程贝塞尔曲线绘制一个圆时。项目中的方法是绘制4个1/4圆,每次用三次贝塞尔绘制1/4圆须要四个点。
这张图中的(0,0)是我们的起始点(1,1)是终点 这两个点都是圆上的能够知道坐标。所以要算出(x1,0)(1,y1)这两个点的坐标。
这就是magicNumber的由来。我们将这个圆的圆心与(x1,0)(0,0)连线。两条线的夹角为20°,由此可算出x1的坐标。
同理y1,这个坐标值为magicNumber。
四个点坐标算出来就能够画圆了。







 本文详细解析了如何使用三次贝塞尔曲线绘制圆形的过程。通过Path.cubic()方法,介绍了如何确定控制点来完成圆的绘制,并解释了magicNumber的概念及其在实际应用中的意义。
本文详细解析了如何使用三次贝塞尔曲线绘制圆形的过程。通过Path.cubic()方法,介绍了如何确定控制点来完成圆的绘制,并解释了magicNumber的概念及其在实际应用中的意义。

















 1884
1884

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








