图解欧几里德算法

今天我吃饼干的时候想到了欧几里德算法的一种图形意义,上网一查，早已经有人发表了一样的想法.

这是广州大学计算机科学与教育软件学院的黄勇发表的欧几里德算法的几何意义的一篇文章.整篇文章只有一个想法，因此这个问题还有很大的探索余地.下面我一一探索.

 

考察面积

已知正整数$a,b$,其中$a<b$,对$a,b$实施欧几里德算法,得到

$$b=q_1a+r_1$$

$$a=q_2r_1+r_2$$

$$r_1=q_3r_2+r_3$$

$$\vdots$$

$$r_n=q_{n+2}r_{n+1}+r_{n+2}$$

$$\vdots$$

我们知道,迟早会有$r_k=0$.

把以上代数过程表达成如下图示:

 

 

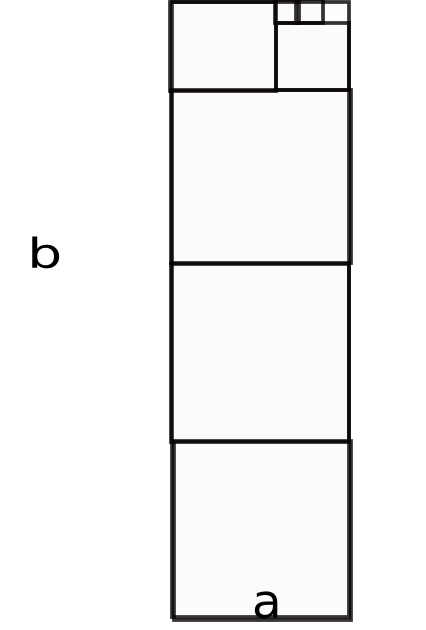
 然后我们考虑面积，易得

$$ab=q_1a^2+q_2r_1^2+q_3r_2^2+\cdots+q_{n+1}r_n^2+\cdots+q_{k}r_k^2$$

举一个具体的例子,令$a=7,b=32$,则$ab=224$.我们知道

$$32=4\times 7+4$$

$$7=1\times 4+3$$

$$4=1\times 3+1$$

$$3=3\times 1+0$$

因此

$$224=4\times 7^2+1\times 4^2+1\times 3^2+ 3\times 1^2\Box$$

由于任意一个大于1的正整数都可以分解成较大因子和较小因子的乘积，因此任意一个大于1的正整数都可以分解为一列递减的平方数的线性组合.这是十分显然的命题,即使不用图形，我们也可以发现.

 

推广

设$a$和$b$是正实数且$b>a$.易得，当$\frac{b}{a}$是有理数时，可以将图形操作有限次完成,当$\frac{b}{a}$是无理数时，要将图形操作无限次.(如何证明?)

转载于:https://www.cnblogs.com/yeluqing/archive/2012/11/26/3827631.html