【吴恩达机器学习】学习笔记——梯度下降

 梯度下降算法能够帮助我们快速得到代价函数的最小值

算法思路：

• 以某一参数为起始点
• 寻找下一个参数使得代价函数的值减小，直到得到局部最小值

梯度下降算法：

• 重复下式直至收敛（收敛是指得到局部最低点的θ_j后，偏导数的值为零，θ_j不会再改变）
• 并且各参数θ₀,...,θ_n必须同时更新，即所有的θ_j值全部都计算得到新值之后才将参数值代入到代价函数中

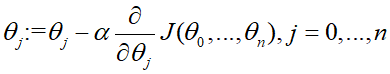
上式中的α是学习速率，决定了θ_j移动的步伐大小。如果α太小，那么θ_j就会更新的很慢；但是如果α太大，θ_j就有可能越过最低点，导致偏导数越来越大，最终远离最低点不收敛。

而上式的偏导数的作用十分巧妙，当θ_j越来越接近局部最低点时，相应地，偏导数会越来越小，因此θ_j更新的幅度会越来越小，直至收敛。

转载于:https://www.cnblogs.com/JJJanepp/p/8454599.html