博弈指什么棋_零和博弈（鞍点理论）：如何找到双方的平衡点？

你好，欢迎来到我的《数学通识50讲》。接下来两讲，我们通过博弈论中最典型的两大类博弈，也就是“零和博弈”与“非零和博弈”来学习博弈论。

博弈论也被称为对策论。从它的名称你能猜想到，它应该是研究在竞争中采用什么样的好策略的理论，但是从本质上讲，它是一套解决最优化问题的方法。

但是，它和传统的最优化问题还不一样，那些问题都有着明确的目标函数或者优化对象，而博弈论所研究的最优化问题有两方甚至多方参与，因此最优化的策略要考虑对方的行为。比如下棋时，你不能总想着吃人家的棋子，还要考虑自己是否会被将死。

博弈论通常被认为是冯·诺依曼发明的。他被认为是比同时代的爱因斯坦还聪明的天才。

尽管如此，冯·诺依曼还是没有能完成对博弈论中非零和博弈的分析，是他的学生纳什解决了这一类问题，纳什并因此获得了诺贝尔经济学奖。关于非零和博弈这个难题，我们下一讲再说，这讲先看零和博弈。

零和博弈如何计算？

所谓零和博弈，就是博弈过程中，一方获利就意味着另一方损失，比如你和朋友吃一张披萨，你多吃一口，他就少吃一口。接下来我们就来看看博弈论是如何解决这类问题的。

我们拿围棋举例说明。为了简单起见，我们就假定X、Y两人下围棋，该X走下一步棋了，他有3种可选的下法。X一方的下法为x1、x2、x3，Y一方的下法也有三种，分别是y1、y2和y3。

在围棋中，一方的所得必然是另一方所失，因此这是一个零和游戏，比如说X走了x1这步棋后，在盘面上的胜率所得是7点，那么Y的胜率损失也是7点。在这样的情形下，我们只要考虑X的胜率变化即可，因为X赢了多少就是Y输的。

我们知道当X采用了x1、x2、x3之中的一种策略后，Y也有相应的三种策略y1、y2和y3，因此它们的组合就有9种结果，就构成了一个3x3的矩阵。在每一个组合中，X有一个胜率的变化，这些变化就构成了矩阵的值：(我们假设这9个结果对应了X能获得的9个分数。)

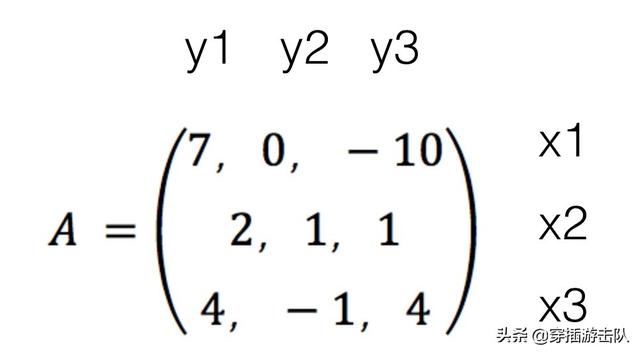
在这个矩阵中，你可以看到，当X采用x1策略时，他最好的情况是碰上Y采用y1，这时X的胜率就增加7点，但是如果Y是一个高手，他采用了y3策略应对，你可以看到X的胜率就小了10点。因此X如果考虑到Y可能的应对策略，他就应该知道，x1其实不能算是一步好棋。

相比之下，采用x2策略就稳健得多，因为无论Y如何应对，他至少可以让自己的胜率增加一点。至于x3，因为有胜率减少一点的可能性，也没有x2好。因此，在制定策略时，如果我们不考虑对方的应对，显然x1是最好的，x2是最差的，但是考虑到对方应对的情况，可能最好和最差的策略就反过来了。

具体到博弈这件事，特别是计算机博弈，最通用的策略是，“在对方给我们造成最糟糕的局面里，选择相对最好的”。也就是说，我们要把x1、x2和x3所有策略算出来后，在可能得到的最糟糕结果中进行比较，具体到这个问题，就是-10、1，和-1这三个结果，然后排序找到最大的，那就是1。在计算机算法中，这种策略被称为最小值中的最大值策略。

接下来我们站在Y的角度来看看他的选择。我们假设他先行棋后，胜率变化的矩阵还是上面那个，当然负值表示他的胜率上升。如果他选择y3，虽然可能让胜率增加10点(对应-10那个值)，但是，也冒着损失4点的风险。相比之下，y2的选择就比较好，因为最不济也不过让胜率损失1个点。类似的，可以分析出来y1也不如y2。

找到平衡点

在很多博弈中，比如谈判中，其实是双方同时选择，并非你出完牌以后，我再出牌，这种情况被称为静态博弈。和它相对的是动态博弈，也就是类似刚才说的下围棋的情况，大家交替出招。

关于静态博弈，我们就可以用上面的矩阵来度量双方的得失。只要X和Y是理性的人，他们就都会发现，其实矩阵中(2，2)位置的那个点对双方来讲都是可以接受的，因为谁都不敢保证自己得到的结果比选择那个点更好。

如果我们把上面的矩阵画在一个三维的图中，就会发现它是一个马鞍形，而位置为(2，2)的这个点，正好是马鞍点。也就是说，这个点从X的角度看，它是所有最低点中的最高点。从Y的角度看，它是所有最高点中的最低点。X追求数值最大，Y追求数值最小，于是这个马鞍点就是一个平衡点(equilibrium)。

上面矩阵的三维视图不好画，我画一个简单的马鞍图，注意一下上面的红点，那就是马鞍点，或者说平衡点。

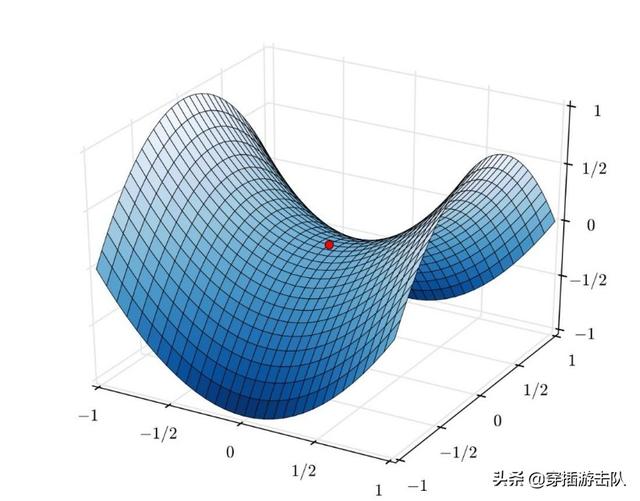
在两方的博弈中，大家其实就是在寻找马鞍点这样一个平衡点，因为大家都知道，如果自己走出了这个平衡点，试图扩大自己的利益，对方就会有反制手段，让自己的利益受损。

当然并非所有的问题里这样的平衡点都在。比如前面那个对弈的胜率矩阵，如果里面的数字都是些很大的正值，也就是说X的实力可以秒杀Y，采用什么策略可能Y都无法应对，这种情况其实不用担心。但是当参与方的水平势均力敌，不相上下时，很多时候寻找最小值中的最大值才是最好的出路，或者说其实双方必然会被锁死在那个平衡点上。

但是，我要特别提醒你的是，在上述的对弈问题中，还有两点需要说明。

• 首先我们其实作了一个隐含的假定，就是双方下棋的策略都是透明公开的，即X和Y都知道对方所有可能的选择，也就是说一切是阳谋，不是阴谋。双方所不知道的，无非是对方最终采取的策略。
• 其次，双方都足够精明，能够判断出该采用什么策略。

不过在真的下棋时，更可能是另一种场景，一个臭棋篓子看不出隐藏得比较深的好棋，会采用比较糟糕的策略，而高手在掂量出对方水平之后，会采用比较激进的下法，每一步占最大的便宜。这种情况，其实就是将对方采用各种策略的概率考虑进去了。

我们还是以上面例子的胜率矩阵来说明问题。假定X知道自己行棋后，Y采用y1、y2和y3策略的概率分别是70%、20%和10%，这时他采用x1的下法反而是最好的。当然，如果是Y先行棋，他可能也会根据X采用不同策略的概率，制定自己的策略。

在静态博弈中有一种非常有趣的情况，那就是双方都知道对方采用各种策略的可能性，这时双方要重新计算平衡点，而这个平衡点和矩阵中的马鞍点未必相同。

多人博弈的投篮问题

由于人们通常在讲博弈论时所举的例子，都是两个人博弈，各自寻找最佳策略的场景，因此很多人误以为博弈论所要解决的只是这一类问题。其实，博弈论研究的问题有很多种类型，比如我们来看看下面这个问题，它也被称为投篮问题。

我们假定有10个选手投篮，投篮的准确性和投手到篮筐的距离有关，离得越近投中的概率越大，最后如果站到篮下，命中率是100%。

比赛的规则是这样的。第一个选手站的位置离篮筐9米，如果他投进去了，比赛结束，他就是赢家；如果没有投进去，第二个人在8米处投篮，如果他投进去就赢得比赛，否则就由第三个人在7米处投篮，这样投下去，直到有一人投中成为赢家。

现在的问题是，你如果参加比赛，该第几个出场？这也是一个博弈论的问题，至于该第几个出场，其实是要看命中率和距离之间的关系。

比如，我们假设它们的关系是这样的：投篮的命中率就是距离加1的倒数，比如第一个人站在9米处，他投中的概率就是1/(9+1)=1/10，第二个人站得更近，所以投中的概率就是1/(8+1)=1/9。类似的，第三个人是1/8，最后一个人是1。你如果这么单纯比较命中率，似乎是最后一个人占便宜。但其实在这种条件下，所有人命中赢球的可能性都相等，都是0.1。

计算这个问题，就要用到我们前面讲到的条件概率了。我们以第二个人为例，他获胜的可能性是：首先第一个人没有投中，其次，他投中了。因此，计算获胜的概率=他的命中率*第一个人失败的概率，即1/9x0.9，还是1/10。类似的，大家可以算出来每个人获胜的概率都是1/10。

这个问题的一个典型例子就是抽签。很多人觉得，如果10个人抽一个大奖，先抽签的人吃亏，因为抽中的概率很小，等到前面那些人没有抽中出局了，我再抽，就不是10抽1，可能是5抽1，甚至是3抽1了。但是这些人只考虑了别人没抽中的情况，忽视了可能奖品已经被抽走的可能性。

当然，在另一些距离和命中率的关系里，结果可能就不同了，比如命中率是距离加1的倒数的平方，这时可以证明，最后一个出场的人获胜的概率最大。

在职场中，什么时候站出来讲话，什么时候站出来接受任务，其实也是有讲究的。站出来太早，可能会失败，站出来太晚，可能别人已经把事情做好了。对我们来讲，最好的情况是，前面有几个人做失败了，而我们临危受命成功了。这其实就是投篮问题的具体应用。

要点总结：

首先，虽然每一个人都希望最大化自己的利益，但是更有意义，更能保证自己利益的，是达成各方面的平衡。在选择策略时，不要老考虑对自己有利的情况，而低估对手可能的策略，要多考虑下行风险，要在所有的最小值中，寻找最大值。在出手做事情时，包括创业时，要根据任务的难度，把握好承担任务的时间。开始的时候失败率高，太晚的时候已经没有了机会。

在有博弈论之前，很多人对这些道理有感性的认识，但是不准确。有了博弈论，将上述问题量化建立数学模型，就有了理性的指导，这便是博弈论的意义。

下一讲，我们来讲博弈论中的大难题，非零和博弈。——吴军《数学通识五十讲》感兴趣的可以去得到订阅