C++实现无标度网络构建与模拟教程

本文还有配套的精品资源，点击获取

简介：无标度网络是一种现实世界广泛存在的复杂网络模型，具有幂律分布的节点度和高度的鲁棒性及可扩展性。本文介绍了如何在C++中实现无标度网络的构建，包括Barabási-Albert模型、Erdős-Rényi模型和Forest Fire模型。同时，讲述了如何模拟无标度网络上的传播现象，如疾病和信息扩散，并强调了中心节点在传播过程中的重要性。本文还指出了使用数据结构、随机数生成器和节点状态更新队列等关键技术点，以及理解无标度网络特性和C++算法的重要性。

1. 无标度网络特性介绍

无标度网络（Scale-Free Network），作为一种复杂网络模型，其最显著的特征是节点的度（即与该节点相连的边的数量）分布遵循幂律分布，这种分布表明网络中存在少数具有极高连接度的节点，即“枢纽节点”或“集散节点”，而绝大多数节点的连接度则相对较低。无标度网络的这一特性，使其在真实世界中广泛存在，从互联网到社交网络，再到生物网络，无标度特性均发挥着关键作用。这种网络结构的存在为理解网络的演化过程、拓扑性质以及抗毁性、信息传播等多种现象提供了重要的理论支持。

无标度网络的特性分析

从理论角度分析，无标度网络的特性主要包括以下几点：

• 幂律分布 ：无标度网络的节点度分布可以用幂律方程来描述，即 (P(k) \sim k^{-\gamma})，其中 (P(k)) 为度为 (k) 的节点出现的概率，(\gamma) 是幂律指数，通常这个指数在2到3之间。
• 抗毁性 ：与随机网络相比，无标度网络对随机故障表现出较强的抗毁性，即删除节点后网络结构依然稳定。然而，针对枢纽节点的故意攻击，无标度网络则较为脆弱。
• 信息传播 ：无标度网络中信息传播的效率较高，枢纽节点的存在使得信息能够快速扩散至整个网络。

无标度网络研究的深入为解决真实世界中的诸多问题提供了新的视角与工具。在本文后续章节中，我们将详细探讨无标度网络的模型实现，包括经典的Barabási-Albert模型、Erdős-Rényi模型的调整以及Forest Fire模型的模拟，为读者展现无标度网络在各个方面的应用。

2. Barabási-Albert模型实现

Barabási-Albert (BA) 模型是用于生成无标度网络的简单模型，其核心思想是网络中的节点增长以及新加入节点倾向于与已有节点中度数较高的节点建立连接。本章节将探讨BA模型的基本原理和如何使用C++进行实现。

2.1 Barabási-Albert模型基本原理

2.1.1 理论背景与模型起源

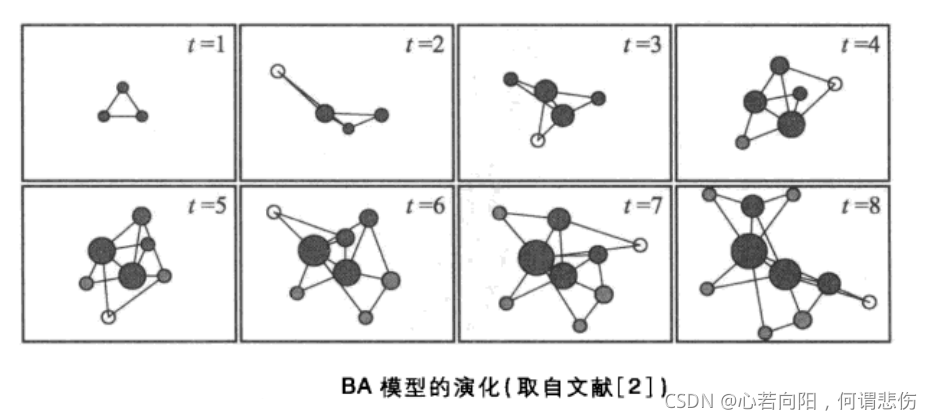
Barabási-Albert模型由Albert-László Barabási和Reka Albert在1999年提出，目的是为了解释现实世界中某些网络的度分布不服从泊松分布，而是呈现幂律分布。该模型基于“偏好依附”的理念，即网络的增长过程中，新节点更倾向于连接到已经拥有较多连接的节点。

2.1.2 模型的数学描述和特性分析

数学上，Barabási-Albert模型可以表示为以下步骤：
1. 初始网络由m0个节点组成。
2. 在每一步中，向网络中添加一个新节点，并与m（m≤m0）个已存在的节点建立连接。
3. 新节点与现有节点建立连接的概率与目标节点的度数成正比，即概率为ki/∑kj，其中ki是目标节点的度数，∑kj是所有节点度数之和。

Barabási-Albert模型的特性分析显示网络具有自组织临界性，因此会自然地形成无标度特性，即网络的度分布遵循幂律分布。

2.2 Barabási-Albert模型的C++实现

2.2.1 数据结构选择与设计

在C++中实现BA模型时，需要选择合适的数据结构来存储节点和边的信息。由于BA模型是一个动态网络，我们通常使用邻接表来表示网络，因为它在动态添加边时具有较高的效率。

#include <vector>
#include <list>
#include <algorithm>
#include <random>
#include <iostream>

// 图的数据结构表示
class Graph {
public:
    Graph(int size) : m_num_nodes(size) {
        for (int i = 0; i < size; ++i) {
            m_adj_list.push_back(std::list<int>());
        }
    }

    // 添加边，连接两个节点
    void add_edge(int node1, int node2) {
        m_adj_list[node1].push_back(node2);
        m_adj_list[node2].push_back(node1); // 无向图
    }

    // 获取邻接表
    std::vector<std::list<int>>& get_adj_list() {
        return m_adj_list;
    }

private:
    int m_num_nodes;
    std::vector<std::list<int>> m_adj_list;
};

2.2.2 关键算法逻辑与代码实现

在实现BA模型时，我们需要一个算法来模拟“偏好依附”的过程。以下是C++代码的一个示例：

// 偏好依附的函数实现，根据已有的节点度数来确定新节点连接的概率
double preferential_attachment(int nodeDegree, int totalDegreeSum) {
    return static_cast<double>(nodeDegree) / totalDegreeSum;
}

// 实现Barabási-Albert模型的函数
Graph build_ba_model(int numNodes, int edgesPerNode) {
    Graph ba_graph(0);
    std::vector<int> degrees(numNodes, 0);
    std::mt19937 generator;
    std::uniform_real_distribution<double> distribution(0.0, 1.0);
    int existing_nodes = 0;

    // 初始网络构建
    for (int i = 0; i < numNodes; ++i) {
        if (i > 0) {
            ba_graph.add_edge(existing_nodes - 1, i);
            for (int j : ba_graph.get_adj_list()[i]) {
                degrees[i] += 1;
                degrees[j] += 1;
            }
        } else {
            ba_graph.add_node(i);
            existing_nodes += 1;
        }
    }

    // 偏好依附连接过程
    for (int i = numNodes; i < numNodes * (numNodes - 1) / 2; ++i) {
        double sum = 0.0;
        for (int j = 0; j < existing_nodes; ++j) {
            sum += degrees[j];
            if (preferential_attachment(degrees[j], sum) > distribution(generator)) {
                ba_graph.add_edge(existing_nodes, j);
                degrees[existing_nodes] += 1;
                degrees[j] += 1;
                break;
            }
        }
        existing_nodes++;
    }

    return ba_graph;
}

在这段代码中，我们首先初始化了一个图 ba_graph 和一个度数数组 degrees 。接着构建了初始网络并为每一步中的新节点执行了偏好依附算法。当添加新边时，我们使用了一个均匀分布的随机数生成器来决定连接的节点。上述代码展现了BA模型生成过程中关键步骤的具体实现。

3. Erdős-Rényi模型调整实现

3.1 Erdős-Rényi模型基础分析

3.1.1 模型的定义与基本特性

Erdős-Rényi模型（简称ER模型），由匈牙利数学家保罗·埃尔德什和阿尔弗雷德·雷尼提出，是一种随机图模型。在ER模型中，图由n个节点组成，每一对不同的节点之间都有一个固定的概率p独立地建立一条边，也就是说，任何两条特定的节点之间可能有也可能没有边，并且所有边的出现都是相互独立的。该模型构建出的网络是完全随机的，其主要特性包括：

• 无特征 ：ER模型不考虑节点的度，因此所有节点都是等价的。
• 均匀分布 ：边的存在概率是均匀的，每个节点的度分布遵循泊松分布，当网络规模较大时，近似为正态分布。
• 无聚集性 ：任意节点的邻居节点彼此之间相互独立，不存在社区结构。

与Barabási-Albert模型对比，ER模型不具有无标度性质，即其节点度分布不是幂律分布。因此，在某些特定的应用场景，例如模拟社交网络时，ER模型可能不太适合，因为它没有反映现实世界中的网络特性，例如“富者更富”的现象。

3.1.2 与Barabási-Albert模型的对比

Barabási-Albert模型和Erdős-Rényi模型在构建网络时采用的方法截然不同。Barabási-Albert模型更关注网络的生长过程和节点的优先连接特性，而ER模型则侧重于随机性，每条边的出现完全随机，不受节点度的影响。这两个模型的主要区别可以总结如下：

• 生长机制 ：BA模型通过网络的生长机制产生无标度网络，而ER模型通过随机连接产生均匀网络。
• 度分布 ：BA模型的节点度分布遵循幂律分布，具有无标度特性；ER模型的节点度分布遵循泊松分布，随网络规模的增大接近正态分布。
• 网络聚集性 ：BA模型因为优先连接机制，往往具有较高的聚集性，而ER模型由于其随机特性，聚集性较低。
• 健壮性 ：由于BA模型网络节点间连接不均匀，具有少量“枢纽”节点，导致其对攻击更为脆弱；而ER模型由于连接均匀，对随机攻击具有较好的健壮性。

3.2 调整后的Erdős-Rényi模型C++实现

3.2.1 代码逻辑的优化和调整

在对Erdős-Rényi模型进行C++实现时，需要考虑代码的性能和可扩展性。以下是一个简化的代码示例，展示如何创建一个基本的ER模型，并生成一个随机图：

#include <vector>
#include <random>

// 生成Erdős-Rényi随机图
std::vector<std::vector<int>> generateERGraph(int n, double p) {
    std::random_device rd;
    std::mt19937 gen(rd());
    std::bernoulli_distribution d(p);

    std::vector<std::vector<int>> graph(n, std::vector<int>(n, 0));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            if (i != j && d(gen)) {
                graph[i][j] = graph[j][i] = 1;
            }
        }
    }
    return graph;
}

在这个函数中，首先使用了C++标准库中的 <random> 头文件中的功能来生成随机数。 std::random_device 用以生成一个非确定性的随机数种子， std::mt19937 是一个基于Mersenne Twister算法的伪随机数生成器，而 std::bernoulli_distribution 则是创建一个伯努利分布实例，用于生成概率为 p 的随机0或1。

代码优化通常涉及减少不必要的操作和空间使用。在此代码中，为了提高效率，我们使用邻接矩阵表示图，并且只在 i 不等于 j 的情况下考虑生成边，避免了自环的出现。此外，图的创建是通过双层循环完成的，这在稀疏图中可能不是最优的，但对于随机图的生成来说，这种直观的实现方式已经足够有效。

3.2.2 实现过程中的性能考量

在上述代码中，主要的性能考量点包括：

• 随机数生成 ：通过使用 std::mt19937 生成器而非简单随机函数，代码能够生成高质量的随机数，并且速度较快。
• 空间使用 ：使用邻接矩阵存储图，这对于小规模网络来说通常是合适的，但对于大规模网络来说，会使用大量的内存。在这种情况下，可以考虑使用邻接表来节省空间。
• 计算复杂度 ：对于大规模网络，使用双层循环构建邻接矩阵的计算复杂度较高。在实际应用中，可以考虑使用稀疏矩阵存储结构，或者使用更高效的算法来减少计算时间。

在调整实现时，我们还可以考虑以下优化：

• 多线程处理 ：对于并行构建图的过程，可以考虑使用多线程。例如，可以将节点分配给不同的线程，每个线程独立计算节点的邻接信息，然后合并结果。
• 向量化操作 ：使用现代CPU的向量化指令，如SIMD（单指令多数据），可以在某些循环中显著提高性能。

这些优化可以进一步提高代码的执行效率，尤其在处理大规模网络模拟时显得尤为重要。但需要注意，过度优化可能会导致代码复杂度增加，应根据实际需求进行权衡。

4. Forest Fire模型模拟实现

4.1 Forest Fire模型概述

4.1.1 模型的基本概念与核心思想

Forest Fire模型是一种用于生成无标度网络的算法，其核心思想基于“森林火灾”的隐喻。在这个模型中，网络的节点可以类比为树木，而边则可以看作是树木之间的连接。与现实中的森林火灾相似，一旦网络中的一棵树被点燃，火焰将沿着相邻的树蔓延，直到没有可燃物为止。Forest Fire模型将这一过程抽象化，用以构建网络。

在Forest Fire模型中，新节点的加入具有以下两个主要特征：探索（Exploration）和扩张（Explosion）。首先，新节点通过探索过程与已存在的少量节点相连，这代表了网络中的少量强连接；随后，扩张过程会导致新节点与大量现有节点相连，这代表了网络中的大量弱连接。这种结合了“少量强连接，大量弱连接”特性的模型，与现实世界中的社会网络相符合，有助于模拟真实世界中网络的增长过程。

4.1.2 模型在无标度网络中的应用

Forest Fire模型在无标度网络中的应用主要体现在其能够生成具有幂律度分布特性的网络，即网络中大部分节点的连接数很少，而少数节点具有大量的连接。这种特性使得Forest Fire模型成为研究社会网络、互联网结构、生物网络等复杂系统的重要工具。

通过模拟Forest Fire模型，可以进一步分析网络的聚集性、连通性以及网络上的信息流动特性等。在实际应用中，Forest Fire模型可用于优化网络设计，提升网络的鲁棒性，以及在疾病传播模型中模拟信息或病毒在网络中的传播路径。

4.2 Forest Fire模型的C++模拟

4.2.1 网络生成与参数设置

为了在C++中实现Forest Fire模型，我们需要定义一些关键参数，如网络的大小、探索概率（p）和扩张概率（q）。探索概率影响新节点探索现有节点的能力，而扩张概率则控制着新节点能扩散到的节点数量。这两个参数共同决定了网络的结构特性。

模拟开始时，需要初始化网络结构和相关参数，具体步骤如下：

1. 初始化网络的节点总数，边总数，探索概率p和扩张概率q。
2. 创建一个空网络结构，这通常使用邻接列表或邻接矩阵来表示。
3. 随机选择一个或多个种子节点作为网络的起始点。

代码示例：

#include <vector>
#include <random>
#include <iostream>

// 定义节点和边的结构体
struct Node {
    int id; // 节点ID
    std::vector<int> neighbors; // 邻接列表
};

// 初始化网络
void initializeNetwork(std::vector<Node>& network, int numNodes, double p, double q) {
    std::default_random_engine generator;
    std::uniform_real_distribution<double> distribution(0.0, 1.0);
    // 创建初始节点
    for (int i = 0; i < numNodes; ++i) {
        network.push_back({i, {}});
    }
    // 连接初始节点
    for (int i = 0; i < numNodes; ++i) {
        if (distribution(generator) < p) {
            // 探索过程，连接少数节点
            // 这里可以根据实际情况来选择具体的连接策略
        }
    }
    // Forest Fire模型的核心部分，模拟扩张过程
    for (int i = 0; i < numNodes; ++i) {
        if (distribution(generator) < q) {
            // 扩张过程，连接大量节点
            // 这里需要定义如何根据当前节点和网络结构来选择目标节点
        }
    }
}

在这段代码中，我们首先定义了节点和边的结构体，然后使用了标准库中的随机数生成器来模拟概率过程。实际代码中需要填充探索和扩张的具体实现逻辑，并且可能需要加入更多的参数设置和状态维护。

4.2.2 模拟运行与结果分析

在模拟Forest Fire模型的运行过程中，我们需要记录网络的演化，包括每次添加节点后网络的拓扑结构变化以及最终网络的统计特性。这些数据可以用来分析网络的度分布、平均路径长度、聚集系数等关键指标。

模拟完成后，我们可以使用图形化工具对网络结构进行可视化展示，从而直观地理解模型的生成结果。同时，通过分析关键指标，我们可以验证模型是否成功地生成了预期的无标度特性。

为了实现结果分析，我们可以采用以下步骤：

1. 在每次添加节点后，记录网络的相关统计信息。
2. 绘制度分布图，检查是否符合幂律分布。
3. 计算聚集系数和平均路径长度等其他网络特性。

对于可视化和结果分析，可以考虑使用如Gephi、Cytoscape等专业图形化工具，也可以通过Matplotlib、Plotly等数据可视化库在Python中进行。

通过模拟运行和结果分析，我们可以更深入地理解Forest Fire模型在无标度网络中的应用，为研究网络的演化机制和动态特性提供数据支持和理论依据。

5. 疾病和信息传播模拟

在现代社会，疾病和信息的传播是两个密切相关且非常重要的研究领域。随着网络技术的快速发展，研究者们开始利用计算机模拟技术来模拟和分析这些传播过程，尤其在无标度网络中，由于其节点分布的非均匀性，这些模拟变得异常复杂但又充满挑战性。本章节将深入探讨模拟疾病和信息传播的基本理论基础，以及如何使用C++实现这些模拟过程，并讨论模拟中遇到的关键问题及解决方案。

5.1 疾病传播模型的理论基础

5.1.1 SIR模型介绍与无标度网络的关系

SIR模型是经典的流行病学模型之一，用于描述疾病传播过程中的三个主要群体：易感者(Susceptible)、感染者(Infectious)和移除者(Removed)。每个群体中的个体在模型中随时间演变，形成动态的群体转换过程。无标度网络的特性使得这些群体之间的连接不再均匀，导致疾病传播的路径和速度都有可能发生根本性的变化。理解SIR模型在无标度网络中的应用是本章讨论的基础。

5.1.2 信息传播模型概述

信息传播模型则是从另一个角度研究信息如何在网络中传播扩散，常见的如独立级联模型（ICM）和线性阈值模型（LTM）。这类模型在信息科学和市场营销等领域有着广泛的应用。在无标度网络中，信息的传播同样受到网络拓扑结构的影响，理解其传播特性有助于提升信息传播效率。

5.2 模拟疾病和信息传播的C++实现

5.2.1 模拟环境设置

为了模拟疾病和信息的传播，首先要设置一个适合的模拟环境。在C++中，这通常涉及到数据结构的选择、参数的初始化以及网络拓扑的生成。

#include <iostream>
#include <vector>
#include <random>

// 定义网络节点结构
struct Node {
    int state; // 状态变量，可以是S（易感者）、I（感染者）或R（移除者）
    double infectionProbability; // 感染概率
};

// 初始化网络节点状态
void initializeNetwork(std::vector<Node>& network, int size, double infectionProb) {
    for (int i = 0; i < size; ++i) {
        network[i].state = Susceptible; // 初始状态为易感者
        network[i].infectionProbability = infectionProb;
    }
    // 可以在此基础上设置几个初始感染者
    network[0].state = Infected;
    // ...其他感染者设置
}

上述代码展示了如何初始化网络节点以及设置初始状态。接下来，要通过模拟循环来更新每个节点的状态。

5.2.2 模拟过程中的关键问题和解决方案

在模拟过程中，面临的关键问题之一是如何高效地更新网络中的节点状态。由于网络通常很大，更新过程需要考虑算法的时间复杂度和空间复杂度。

void updateNetwork(std::vector<Node>& network, int size) {
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_real_distribution<> dis(0.0, 1.0);

    for (int i = 0; i < size; ++i) {
        if (network[i].state == Infected) {
            // 检查每个易感者邻居是否感染
            for (auto& neighbor : network[i].neighbors) {
                if (neighbor.state == Susceptible &&
                    dis(gen) < neighbor.infectionProbability) {
                    neighbor.state = Infected; // 感染邻居节点
                }
            }
        }
    }
}

在上述代码段中，模拟更新节点状态时使用了随机数生成器来决定是否发生传播事件。这种方法在处理大型网络时可能较为低效，因为每个节点的邻居都需要被检查。为了提高效率，可以采用优先队列或其他数据结构来优化邻居节点的选择。

// 使用优先队列优化感染过程
void optimizedUpdate(std::vector<Node>& network, int size) {
    // ...此处代码省略，但应包含优先队列的使用，以高效选择感染节点的邻居
}

通过优化算法逻辑，我们可以减少不必要的检查，从而提高整个模拟的效率。例如，优先队列可以帮助我们首先更新那些最有可能传播疾病的节点，这可以显著提高仿真效率。此外，对于并行计算的支持也是优化的关键方向之一，利用现代多核处理器的优势，可以大大加速模拟过程。

通过本章的介绍，我们了解到疾病和信息传播模拟的重要性，以及如何在C++环境中实现这一模拟。我们还讨论了模拟过程中可能遇到的关键问题以及如何使用数据结构、算法优化和并行计算等手段来解决这些问题。希望本章能够帮助读者在无标度网络疾病和信息传播模拟方面取得更深入的理解。

6. 数据结构使用（图，邻接矩阵/邻接表）

6.1 图的数据结构基础

6.1.1 图的定义与性质

图（Graph）是由顶点（Vertex）的集合和边（Edge）的集合组成的数据结构，用于表示元素之间的关系。在无标度网络中，图的结构通常用于描述网络中节点之间的连接关系。图的定义包括：

• V(G)：表示图G的顶点集合，每个顶点代表网络中的一个节点。
• E(G)：表示图G的边集合，每条边代表节点间的连接关系。
• 无向图：边不区分方向，表示节点间的双向关系。
• 有向图：边有明确的方向，表示节点间的单向关系。
• 加权图：边上有权重，表示节点间关系的强度或成本。

图的性质主要体现在顶点和边的特性上，比如度（Degree）是指一个顶点连接的边的数量，路径（Path）是指顶点序列中相邻顶点通过边相连形成的序列。

6.1.2 邻接矩阵与邻接表的比较

在图的表示方法中，邻接矩阵和邻接表是两种常见的实现方式：

• 邻接矩阵（Adjacency Matrix）：使用二维数组来表示图，其中图的每个顶点都与一个矩阵行和列相对应。邻接矩阵中的元素表示顶点之间的连接关系，一般用1表示相连，用0表示不相连。如果图是有向的，则可以区分出出度和入度。

• 优点 ：直观，易于判断任意两个顶点是否相连。

• 缺点 ：空间复杂度较高，对于稀疏图来说会浪费较多空间。

• 邻接表（Adjacency List）：使用链表来存储每个顶点的邻接信息。每个顶点都有一个链表，链表中存储了所有与该顶点相邻的其他顶点。

• 优点 ：节省空间，尤其适合表示稀疏图。

• 缺点 ：不直观，需要遍历链表来判断顶点间的连接。

在无标度网络中，根据网络的密度和图的规模选择合适的数据结构显得尤为重要，因为不同的数据结构对后续的网络分析和算法实现有直接影响。

6.2 图的数据结构在无标度网络中的应用

6.2.1 图结构的选择与理由

在无标度网络的模拟与分析中，选择合适的数据结构是关键一步。选择图结构时需要考虑以下几个因素：

• 网络规模：对于小规模网络，邻接矩阵可以提供快速的访问速度。对于大规模网络，邻接表则能节省内存空间。
• 网络密度：对于稀疏网络，邻接表是更优的选择，因为它可以有效地存储非连接信息。
• 操作类型：如果网络操作频繁涉及顶点间的连接检查，邻接矩阵可能更为合适，因为它的查找操作时间复杂度较低。

在无标度网络模拟中，通常会优先选择邻接表来表示图结构，因为无标度网络往往是稀疏的，并且许多模拟操作涉及遍历特定顶点的邻接顶点，邻接表在这方面提供了较高的灵活性。

6.2.2 实现中的空间与时间效率优化

在C++中，使用邻接表可以利用标准模板库（STL）中的 vector 或 list 来实现，这样可以节省内存并且易于操作。

示例代码 - 邻接表的C++实现

#include <vector>
#include <list>

// 图的邻接表表示
class Graph {
private:
    int V; // 顶点的数量
    std::vector<std::list<int>> adj; // 邻接表

public:
    Graph(int V); // 构造函数
    void addEdge(int v, int w); // 添加边
    void printGraph(); // 打印图
};

在 Graph 类的构造函数中初始化邻接表，并在 addEdge 方法中添加边信息。 printGraph 方法则用于打印图的邻接表结构。

// 构造函数
Graph::Graph(int V) {
    this->V = V;
    adj.resize(V);
}

// 添加边
void Graph::addEdge(int v, int w) {
    adj[v].push_back(w); // 添加一个从v到w的边
    // 无向图需要添加以下代码
    // adj[w].push_back(v); // 添加一个从w到v的边
}

// 打印图
void Graph::printGraph() {
    for (int v = 0; v < V; ++v) {
        std::cout << "邻接顶点: ";
        for (auto i = adj[v].begin(); i != adj[v].end(); ++i) {
            std::cout << *i << " ";
        }
        std::cout << std::endl;
    }
}

在实际应用中，为了进一步提高空间效率，可以使用 std::set 代替 std::list 来存储邻接顶点，以避免邻接表中出现重复的边。此外，在遍历图或寻找特定路径时，可以使用深度优先搜索（DFS）或广度优先搜索（BFS）算法，并根据具体需求进行优化。

通过选择合适的数据结构并优化算法实现，可以有效地提升无标度网络模拟的性能和效率。这些优化对于处理大规模网络数据和复杂网络模拟尤其重要，也使得研究人员能够更加深入地探索无标度网络背后的复杂现象。

7. 随机数生成与状态更新

随机数生成与状态更新是复杂网络模拟中的关键技术，它们对于模拟的准确性和效率有着直接的影响。在这一章节中，我们将详细介绍随机数生成的理论与方法，并探讨如何设计状态更新策略以及它们与随机数生成器的结合。

7.1 随机数生成的理论与方法

7.1.1 随机数生成的基本原则

模拟过程中，随机数生成器是必不可少的工具。它负责生成一系列符合特定分布的随机数，模拟实际现象中的随机性。在选择随机数生成器时，需要考虑以下基本原则：

• 均匀性 ：生成的随机数序列应在其定义域内均匀分布。
• 独立性 ：序列中的随机数应相互独立，不应有明显的周期性和相关性。
• 可重复性 ：为了保证实验的可重复性，随机数生成器应该可以设置种子（seed）。
• 高性能 ：生成随机数的速度应足够快，以满足模拟需求。

7.1.2 常用随机数生成器介绍

在实际应用中，有很多现成的随机数生成器可供选择，它们各有优缺点。以下是一些常见的随机数生成器：

• 线性同余生成器 (Linear Congruential Generator, LCG) ：是一种简单的伪随机数生成器，具有速度快、实现简单的特点，但在质量上可能不足以满足复杂模拟的要求。
• 梅森旋转 (Mersenne Twister) ：这是一种周期长且质量高的伪随机数生成器，广泛应用于科学计算和模拟中。
• C++标准库中的 <random> ：C++11引入了一个全面的随机数生成库，它提供了一系列随机数生成器、分布和引擎，使得随机数的生成更加标准化和方便。

示例代码展示如何使用C++标准库中的 <random> 来生成均匀分布的随机数：

#include <random>
#include <iostream>

int main() {
    std::random_device rd;  // 随机数种子生成器
    std::mt19937 gen(rd()); // 以随机数种子生成器为种子的梅森旋转生成器
    std::uniform_int_distribution<> dis(1, 6); // 均匀分布的定义，范围是1到6

    for (int n=0; n<10; ++n) {
        std::cout << dis(gen) << ' '; // 输出10个随机数
    }
    std::cout << std::endl;
    return 0;
}

7.2 状态更新的策略与实现

7.2.1 状态更新算法的设计

在复杂网络模拟中，状态更新是指根据某种规则改变网络中节点或边的状态。例如，在疾病传播模型中，每个节点的状态可能是易感、感染或免疫，状态更新则是指在每个模拟时间步长中，节点可能从易感变为感染，或者从感染变为免疫。

状态更新算法的设计需要基于模型的具体规则，以下是一些常见的策略：

• 同步更新 ：所有节点的状态同时更新，适用于需要保持节点间一致性的场景。
• 异步更新 ：节点状态的更新是随机的，更贴近真实世界中的独立事件。
• 概率更新 ：节点状态的更新取决于一定的概率，这在模拟不确定现象时非常有用。

7.2.2 状态更新与随机数生成器的结合

在实现状态更新算法时，随机数生成器是实现概率更新和随机选择的关键组件。每个节点的状态更新可能需要依赖于一系列随机数，这些随机数决定了更新是否发生以及如何发生。

示例代码展示如何将随机数生成与状态更新结合起来，在一个简化的疾病传播模型中：

#include <vector>
#include <random>

enum class State { Susceptible, Infected, Recovered };

void update_node_state(State &state, double recovery_prob, std::mt19937 &gen) {
    std::uniform_real_distribution<> dis(0.0, 1.0);
    if (state == State::Infected) {
        if (dis(gen) < recovery_prob) {
            state = State::Recovered; // 概率为recovery_prob的节点恢复
        }
    }
}

int main() {
    std::vector<State> nodes = {State::Susceptible, State::Infected, State::Susceptible}; // 三个节点的初始状态
    double recovery_prob = 0.1; // 恢复概率
    std::random_device rd;
    std::mt19937 gen(rd());

    // 更新所有节点状态
    for (State &node_state : nodes) {
        update_node_state(node_state, recovery_prob, gen);
    }

    // 输出更新后的节点状态
    for (const State &node_state : nodes) {
        if (node_state == State::Susceptible) {
            std::cout << "Susceptible ";
        } else if (node_state == State::Infected) {
            std::cout << "Infected ";
        } else {
            std::cout << "Recovered ";
        }
    }
    std::cout << std::endl;
    return 0;
}

在上述代码中，节点的状态根据恢复概率进行更新。这个简单的例子说明了如何将随机数生成器和状态更新结合在一起，在实际的网络模拟中，这种方法会更加复杂和多样化。通过合理选择随机数生成器和设计状态更新策略，我们可以构建出既可靠又有效的模拟系统。

本文还有配套的精品资源，点击获取

简介：无标度网络是一种现实世界广泛存在的复杂网络模型，具有幂律分布的节点度和高度的鲁棒性及可扩展性。本文介绍了如何在C++中实现无标度网络的构建，包括Barabási-Albert模型、Erdős-Rényi模型和Forest Fire模型。同时，讲述了如何模拟无标度网络上的传播现象，如疾病和信息扩散，并强调了中心节点在传播过程中的重要性。本文还指出了使用数据结构、随机数生成器和节点状态更新队列等关键技术点，以及理解无标度网络特性和C++算法的重要性。

本文还有配套的精品资源，点击获取