Bezier - 匀速贝塞尔曲线运动的实现

备注：在网上看到一个讲贝塞尔曲线的例子，觉得不错，自己转过来收藏了。
原作者不详，转载自这里 ：http://www.thecodeway.com/blog/?p=293

二次贝塞尔曲线通常以如下方式构建，给定二维平面上的固定点P0,P1,P2，用B(t)表示该条曲线

用一个动画来演示，可以更加清楚的表明这条曲线的构建过程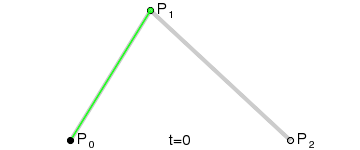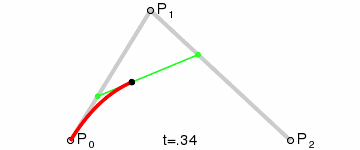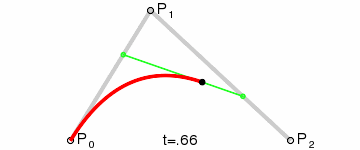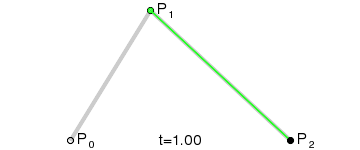






如果t变量本身线形变化的话，这条贝塞尔曲线本身的生成过程是并不是匀速的，通常都是两头快中间慢。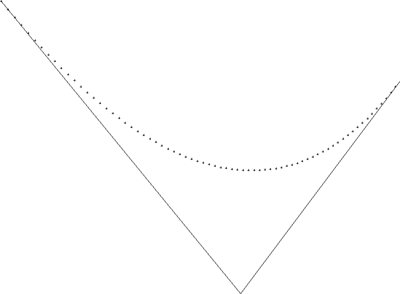




如果t变量本身线形变化的话，这条贝塞尔曲线本身的生成过程是并不是匀速的，通常都是两头快中间慢。

如何想要得到匀速的贝塞尔曲线运动呢？比如我们在某款游戏中设计了一条贝塞尔曲线的路径，如何实现玩家匀速在这条路径上运动呢？
思考这个算法颇费了一番脑筋，其间还得到数学牛人Charlesgao的帮助，非常感谢他（比较糗的是，我问问题的时候就把其中的一个公式搞错了，见笑了-_-!)。

首先需要求得B(t)相对于t的速度公式s(t)


为了简化公式，我们定义如下变量：


计算出的s(t)可以表达为：


其中A,B,C是根据P0,P1,P2计算出的常数：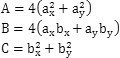


根据这个公式，求得贝塞尔曲线的长度公式L(t)：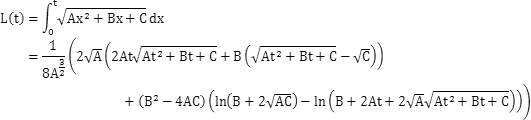


设t`就是能够使L实现匀速运动的自变量，那么显然L(t`)=L(1.0)*t，即：


由于L(t)函数非常复杂，直接求逆函数的表达式几乎不可能，还好我们可以知道它的导数为s(t)，在实际使用中，可以使用牛顿切线法求出近似解。其迭代算法可以表达为：


我写了一个测试程序用于验证该算法，运算结果如下，可以看到，这条曲线已经是以匀速方式生成的了 ^_^：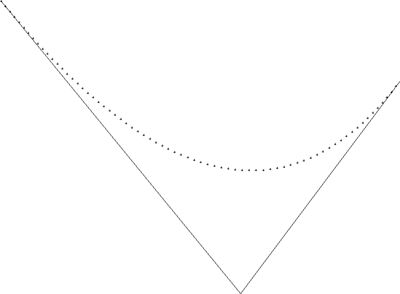


完整的示例源代码附载下面:
下载: Bezeier.cpp (4.2KB)

BezeierCode

    --     --        ---       ---       ---   

--

 

转载于:https://www.cnblogs.com/didi/archive/2009/09/09/1563435.html