逆元讲解（三种方法）

转自：https://blog.youkuaiyun.com/LOOKQAQ/article/details/81282342

【同余的定义】：

 

【同余的主要性质】：

 

 (a+b)%d=(a%d+b%d)%d

 加减乘除都能分开写

 要注意的是减法，因为减法可能会减出来负值所以可以这样写（a-b+mod）%mod；

性质证明：

 

 

【逆元】

（1）定义：

 就是一个数的倒数，那为什么要求一个数的倒数：比如a/b这个时候b的值特别大，就是导致double精度不够所以我们要将a/b换成a*c，其中c^-1=b.

 

【费马小引理求解逆元】：（易知费马定理是有限制的：a与p要互质）

代码实现：（精华就是快速幂）

long long quickpow(long long a,long long b){

 if(b<0)  return 0;

 long long ret=1;

 a%=mod;

 while(b){

  if(b & 1 ) ret = ( ret *a ) % mod

  b>>=1;

  a = (a * a)% mod;

 }

 return ret;

}

long long inv(long long a){

 return quickpow(a,mod-2);

}

 

【扩展欧几里得算法求逆元】：

辗转相除法：

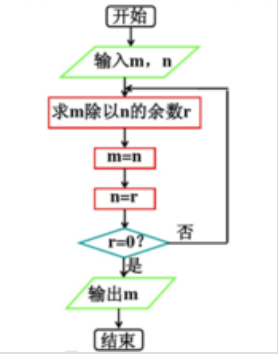
可以来这看看（回溯得到方程解）：https://baike.baidu.com/item/辗转相除法/4625352?fr=aladdin#4

（2）扩展欧几里得算法的证明：

 

（3）求解逆元：

（4）代码实现：

int exgcd(int a,int b,int &x,int &y)

{

 if(b==0)

 { //推理，终止条件1

  x=1;

  y=0;

  return a;

 }

 int t=exgcd(b,a%b,x,y)

   int t=x;

   x=y;

   y=t-(a/b)*y;

   return r;  最大公约数

}

（3）、

但是对于要求好多数的逆元的题目，这样写会超时

我们还有线性求逆元的方法 

来看带余除法 式子 p=k*i+r 

我们可以写成 k*i+r≡0(mod p) 

式子两边同乘 i^-1*r^-1 (i^-1,r^-1皆为模p意义下的逆元) 

所以我们有 k*r^-1+i^-1≡0(mod p) 

i^-1≡-k*r^-1(mod p)

i^-1≡-(p/i)*(p%i)^-1(mod p)

这样我们就线性求得了逆元

代码：

#include <cctype>
#include <cstdio>

typedef long long LL;
const int MAXN=3000010;

int n,p;

LL inv[MAXN];

int hh() {
    scanf("%d%d",&n,&p);
    printf("1\n");
    inv[1]=1;
    for(int i=2;i<=n;++i) {
        inv[i]=(LL)(p-p/i)*inv[p%i]%p;
        printf("%d\n",inv[i]);
    }
    return 0;
}

int sb=hh();
int main(int argc,char**argv) {;}

线性求逆元

 

转载于:https://www.cnblogs.com/kongbursi-2292702937/p/10582258.html