bzoj4869: [Shoi2017]相逢是问候（欧拉函数+线段树）

　　这题是六省联考的...据说数据还出了点锅，心疼六省选手QAQ

　　首先要知道扩展欧拉定理...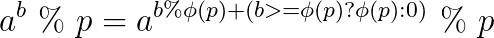

　　可以发现每次区间操作都会使模数进行一次phi操作，而一个数最多取logp次phi就会变成1，这时后面的指数就没有用了，以后这个数的答案就不会变化了，也就是说一个数最多只会进行log次修改，那么我们就可以用线段树维护，如果某棵子数的最小操作次数达到了使模数变成1的次数我们就不需要修改了。

　　但是我们发现快速幂还有一个log，如果不优化的话三个log很有可能TLE。这个时候就有新操作了，底数是一定的c，指数最大为1e9，那么我们可以预处理出c^1~c^10000，设t为c^10000，再预处理出t^1~t^10000，这样对于每个询问我们只需要拆成前后两部分分别在c和t的表里找到并乘起来就好了，这样之后一个点最多被修改logn次，线段树效率O(NlogN)，总复杂度O(Nlog^2N)。

　　要注意的点（数据出锅的地方）是预处理的时候计算使模数变成1的最小操作次数也就是几次幂运算之后答案不变，必须预处理到phi(1)=1，不能预处理到phi(2)=1，因为如果序列中有0的话，它是<phi(2)的，这时候指数加上phi(2)可能会出错。所以需要递归到phi(1)=1的地方，这样即使指数是0，加一之后c^0和c^1都一定>=phi(2)。

　　有一些大爷的博客就给出了只递归到phi(2)=1的反例，如 链接。

　　因为对c进行不同次的幂操作的模数并不同，不能递推，所以要预处理的东西还有c的logp次幂操作，这个可以直接递归计算，因为递归层数不会超过logp，枚举序列中的数和模数为O(NlogN)，快速幂已经预处理了，所以总的复杂度为O(NlogNP)。至于递归的时候如何判断指数是否大于phi(当前模数)，因为2进行4次幂操作之后已经非常大了（远大于p），所以只需要判断接下来的递归次数是否大于5就好了（如果小于5还要判断最顶部那个序列里的数和c进行(递归层数-1)次幂操作的数乘起来是否大于phi(当前模数)）。

　　还要预处理的就是p进行logp次操作途中的所有phi值，然后这题就完了

#include<iostream> 
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath> 
#include<algorithm> 
#define MOD(x) ((x)>=mod?(x)-mod:(x))
#define ll long long
using namespace std;
const int maxn=500010, inf=1e9;
struct poi{int sum, cnt;}tree[maxn<<2];
int n, m, c, mod, cnt, ty, x, y;
int a[maxn], p[maxn], mi1[30][maxn], mi2[30][maxn], cmi[30][maxn];
inline void read(int &k)
{
    int f=1; k=0; char c=getchar();
    while(c<'0' || c>'9') c=='-'&&(f=-1), c=getchar();
    while(c<='9' && c>='0') k=k*10+c-'0', c=getchar();
    k*=f;
}
inline int min(int a, int b){return a<b?a:b;}
inline void pushup(int x)
{
    tree[x].sum=tree[x<<1].sum+tree[x<<1|1].sum; 
    tree[x].sum=MOD(tree[x].sum);
    tree[x].cnt=min(tree[x<<1].cnt, tree[x<<1|1].cnt);
}
void build(int x, int l, int r)
{
    if(l==r){read(a[l]); tree[x].sum=a[l]; return;}
    int mid=(l+r)>>1;
    build(x<<1, l, mid); build(x<<1|1, mid+1, r);
    pushup(x);
}
inline int phi(int n)
{
    int ans=n;
    for(int i=2;i*i<=n;i++)
        if(!(n%i))
        {
            ans=ans/i*(i-1);
            while(!(n%i)) n/=i;
        }
    if(n>1) ans=ans/n*(n-1);
    return ans;
}
inline int power(int n, int x){return 1ll*mi2[x][n/10000]*mi1[x][n%10000]%p[x];}
inline int getmi(int x, int y, int mod)
{
    if(c==1)return 1; if(!y) return x%p[mod];
    int nxt=min(y, x+5); ll now=(nxt==y?x:c);
    if(now>=p[mod+1]) return power(getmi(x, y-1, mod+1)+p[mod+1], mod);
    for(int i=nxt-1;i>=1;i--)
    {
        ll t=now, now=1; 
        for(int j=1;j<=t;j++)
        {
            now*=c; 
            if(now>=p[mod+1]) return power(getmi(x, y-1, mod+1)+p[mod+1], mod);
        }
    }
    return power(getmi(x, y-1, mod+1), mod);
}
void prepare()
{
    p[0]=mod; while(p[cnt]-1) p[++cnt]=phi(p[cnt-1]); p[++cnt]=1;
    for(int i=0;i<=cnt;i++)
    {
        mi1[i][0]=1; for(int j=1;j<=10000;j++) mi1[i][j]=1ll*mi1[i][j-1]*c%p[i];
        mi2[i][0]=1; for(int j=1;j<=10000;j++) mi2[i][j]=1ll*mi2[i][j-1]*mi1[i][10000]%p[i];
    }
    for(int i=1;i<=n;i++) 
        for(int j=1;j<=cnt;j++) 
            if(a[i]) cmi[j][i]=getmi(a[i], j, 0);
                else cmi[j][i]=getmi(1, j-1, 0);
}
void update(int x, int l, int r, int cl, int cr)
{
    if(tree[x].cnt>=cnt) return;
    if(l==r){tree[x].cnt++, tree[x].sum=cmi[tree[x].cnt][l]; return;}
    int mid=(l+r)>>1;
    if(cl<=mid) update(x<<1, l, mid, cl, cr);
    if(cr>mid) update(x<<1|1, mid+1, r, cl, cr);
    pushup(x);
}
inline int query(int x, int l, int r, int cl, int cr)
{
    if(cl<=l && r<=cr) return tree[x].sum;
    int mid=(l+r)>>1, ret=0;
    if(cl<=mid) ret=query(x<<1, l, mid, cl, cr);
    if(cr>mid) ret+=query(x<<1|1, mid+1, r, cl, cr), ret=MOD(ret);
    return ret;
}
int main()
{
    read(n); read(m); read(mod); read(c); 
    build(1, 1, n); prepare();
    for(int i=1;i<=m;i++)
    {
        read(ty); read(x); read(y);
        if(!ty) update(1, 1, n, x, y);
            else printf("%d\n", query(1, 1, n, x, y));
    }
}

View Code

转载于:https://www.cnblogs.com/Sakits/p/7743582.html