基于比较排序的算法复杂度的下界

最新推荐文章于 2023-10-04 18:01:50 发布

weixin_30745553

最新推荐文章于 2023-10-04 18:01:50 发布

阅读量159

点赞数 1

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/TIMHY/p/10786592.html

本文深入探讨了基于比较的排序算法背后的决策树模型原理，通过数学推导，利用斯特林公式证明了排序算法复杂度的下界为O(nlogn)，并提供了不依赖斯特林公式的替代证明方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2019-04-28 20:51:54

首先，所有基于比较的排序算法，都是以决策树模型作为依据的。

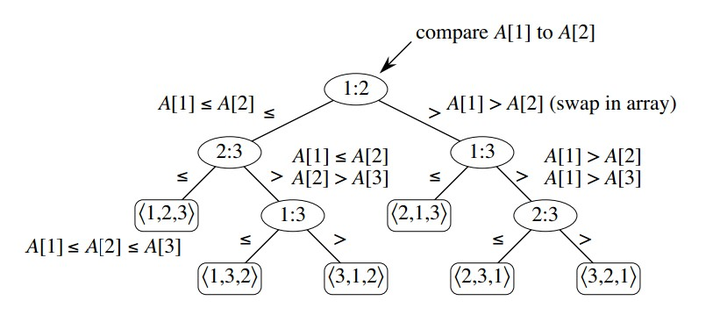
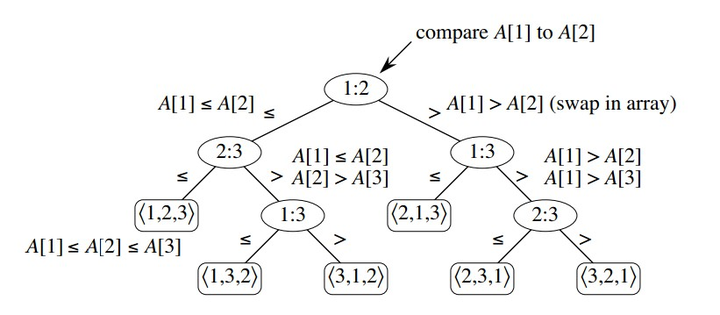
对于待排序的 n 个元素，其所有可能的排序种数为 n! ，其决策树高度为h （即为排序算法比较的次数）
高度为 h 的决策树，最多有叶子节点 $2^{h}$ 个，所以就有 $2^{h}>=n!$
h>=log(n!)

h>=log(n!)

由斯特林近似公式：

$n!=\sqrt{2\pi n} *(\frac{n}{e} )^{n}*(1+\Theta (\frac{1}{n} ))$
得 $h>=\frac{1}{2} log(2\pi)+\frac{1}{2}log(n)+nlog(n)-nlog(e)+log(1+\Theta (\frac{1}{n}))$
其中， $\Theta (\frac{1}{n} )\in \left[ e^{\frac{1}{12n+1} } \,,e^{\frac{1}{12n}} \right]$
故，

的渐近下界为 $\Omega (nlog(n))$

【补充】

如果不使用斯特林公式，依然可以证明得到log(n!)和nlogn是同阶的。

1）显然的是n! < n^n，因此log(n!) < nlogn

2) n! = n * (n - 1) * ... * 1, 我们可以将前n / 2的数字放缩到n / 2，后面的所有数字舍去，因此n! > (n / 2) ^ (n / 2)，得log(n!) > nlog(n)

综上，logn! 和 nlogn是同阶的。

转载于:https://www.cnblogs.com/TIMHY/p/10786592.html

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。