[hdu 2604] Queuing 递推 矩阵快速幂

Problem Description

Queues and Priority Queues are data structures which are known to most computer scientists. The Queue occurs often in our daily life. There are many people lined up at the lunch time. 
  Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2^L numbers of queues. For example, if L = 2, then they are ff, mm, fm, mf . If there exists a subqueue as fmf or fff, we call it O-queue else it is a E-queue.
Your task is to calculate the number of E-queues mod M with length L by writing a program.

 

Input

Input a length L (0 <= L <= 10 ⁶) and M.

 

Output

Output K mod M(1 <= M <= 30) where K is the number of E-queues with length L.

 

Sample Input

3 8 4 7 4 8

 

Sample Output

6 2 1

 

题意：L个人排队，求不含fmf, fff这两种组合的总组合数对M求余的结果。

思路：用后向前看，f(n)为第n个人的取法总和:

　　　1.第n位为m  则前面的可以任意取 即为f(n-1)种取法

　　　2.第n位为f 　第n-1位为f  则第n-2位只能是m  第n-3位也只能是m  第n-4位就可以任意取了  即为f(n-4)种取法

   　　 3.第n位为f　 第n-1位为m  则第n-2位只能为m  第n-3位就可以任意取  即为f(n-3)种取法

　　　可得出递推关系式：f(n) = f(n-1) + f(n-3) + f(n-4)

　　　可以直接用递推求解，不过差点超时，递推可以转化为矩阵的乘法

          

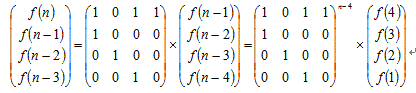
直接递推：

#include <iostream>
#include <stdio.h>
#include <cstring>
#include <algorithm>
using namespace std;

int L, M;

int solve()
{
    int a[1000010];
    a[0] = 1; a[1] = 2;
    a[2] = 4; a[3] = 6;
    for (int i = 4; i <= L; i++) {
        a[i] = a[i-1]+a[i-3]+a[i-4];
        a[i] %= M;
    }
    return a[L];
}

int main()
{
    //freopen("1.txt", "r", stdin);
    while (~scanf("%d%d", &L, &M)) {
        printf("%d\n", solve());
    }



    return 0;
}

矩阵快速幂

#include <iostream>
#include <cstring>
#include <stdio.h>
#include <algorithm>
#include <math.h>
using namespace std;
#define LL long long
const int Max = 4;
int L, M;
struct Mat
{
    LL m[Max][Max];

    void clear() {
        memset(m, 0, sizeof(m));
    }
    
    void Init() {
        clear();
        for (int i = 0; i < Max; i++) 
            m[i][i] = 1;
    }
    
};

Mat operator * (Mat a, Mat b) 
{
    Mat c;
    c.clear();
    for (int i = 0; i < Max; i++)
        for (int j = 0; j < Max; j++)
            for (int k = 0; k < Max; k++) {
                c.m[i][j] += (a.m[i][k]*b.m[k][j])%M;
                c.m[i][j] %= M;
            }
    return c;
}

Mat quickpow(Mat a, int k)
{
    Mat ret;
    ret.Init();
    while (k) {
        if (k & 1) 
            ret = ret*a;
        a = a*a;
        k >>= 1;
    }
    return ret;
}

int main()
{    
    //freopen("1.txt", "r", stdin);
    Mat a, b, c;
    a.clear(); b.clear(); c.clear();
    a.m[0][0] = 9; a.m[1][0] = 6;
    a.m[2][0] = 4; a.m[3][0] = 2;

    b.m[0][0] = b.m[0][2] = b.m[0][3] =
    b.m[1][0] = b.m[2][1] = b.m[3][2] = 1;

    while (~scanf("%d%d", &L, &M)) {
        LL ret;
        if (L == 0)
            ret = 0;
        else if (L <= 4)
            ret = a.m[4-L][0]%M;
        else {
            c = quickpow(b, L-4);
            c = c*a;
            ret = c.m[0][0]%M;
        }
        printf("%lld\n", ret);
    }


    return 0;
}

 

转载于:https://www.cnblogs.com/whileskies/p/7284165.html