[CF431C]k-Tree

题目描述

Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k k k -tree.

A k k k -tree is an infinite rooted tree where:

• each vertex has exactly k k k children;
• each edge has some weight;
• if we look at the edges that goes from some vertex to its children (exactly k k k edges), then their weights will equal 1,2,3,...,k 1,2,3,...,k 1,2,3,...,k .

The picture below shows a part of a 3-tree.

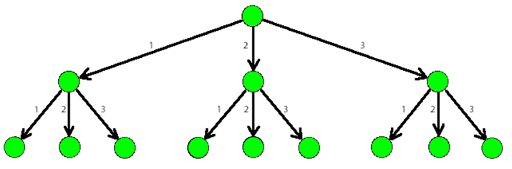
As soon as Dima, a good friend of Lesha, found out about the tree, he immediately wondered: "How many paths of total weight n n n (the sum of all weights of the edges in the path) are there, starting from the root of a k k k -tree and also containing at least one edge of weight at least d d d ?".Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo 1000000007 1000000007 1000000007 ( 109+7 10^{9}+7 109+7 ).

输入输出格式

输入格式：

A single line contains three space-separated integers: n n n , k k k and d d d ( 1<=n,k<=100; 1<=n,k<=100; 1<=n,k<=100; 1<=d<=k 1<=d<=k 1<=d<=k ).

输出格式：

Print a single integer — the answer to the problem modulo 1000000007 1000000007 1000000007 ( 109+7 10^{9}+7 109+7 ).

输入输出样例

输入样例#1： 复制

3 3 2

输出样例#1： 复制

3

输入样例#2： 复制

3 3 3

输出样例#2： 复制

1

输入样例#3： 复制

4 3 2

输出样例#3： 复制

6

输入样例#4： 复制

4 5 2

输出样例#4： 复制

7

---

简单的DP。
设f[i][j][0/1]为目前在深度为i，和为j，是否出现多大于等于d的边的方案数。
然后随便转移。
因为转移比较特色可以省掉第一维。
貌似网上还有别的方法。
f[i][j]表示和为i，出现的最大边权是j的方案数。
f[i+k][max(j,k)] += f[i][j]。

---

#include <bits/stdc++.h>
using namespace std;
#define reg register
#define mod 1000000007
int n, K, d;
int f[105][105][2];
int ans;

int main()
{
    scanf("%d%d%d", &n, &K, &d);
    f[0][0][0] = 1;
    for (reg int i = 1 ; i <= n ; i ++) //dep
    {
        for (reg int j = 1 ; j <= n ; j ++) //tot val
        {
            for (reg int k = 1 ; k <= K ; k ++) //the edge run
            {
                if (j - k < 0) break;
                if (k >= d) f[i][j][1] = (f[i][j][1] + f[i-1][j-k][0]) % mod;
                else f[i][j][0] = (f[i][j][0] + f[i-1][j-k][0]) % mod;
                f[i][j][1] = (f[i][j][1] + f[i-1][j-k][1]) % mod;
            }
        }
    }
    for (reg int i = 1 ; i <= n ; i ++) ans = (ans + f[i][n][1]) % mod;
    cout << ans << endl;
    return 0;
}

 

转载于:https://www.cnblogs.com/BriMon/p/9691036.html