离散化+去重+二分查找

最新推荐文章于 2024-12-16 20:45:27 发布

转载最新推荐文章于 2024-12-16 20:45:27 发布 · 293 阅读

2 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/wkfvawl/p/9343696.html

文章标签：

#数据结构与算法

离散化

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。
通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。例如：
原数据：1,999,100000,15；处理后：1,3,4,2；
原数据：{100,200}，{20,50000}，{1,400}；
处理后：{3,4}，{2,6}，{1,5}；

离散化是程序设计中一个常用的技巧，它可以有效的降低时间复杂度。其基本思想就是在众多可能的情况中，只考虑需要用的值。离散化可以改进一个低效的算法，甚至实现根本不可能实现的算法。要掌握这个思想，必须从大量的题目中理解此方法的特点。例如，在建造线段树空间不够的情况下，可以考虑离散化。

数据的离散化

有些数据本身很大，自身无法作为数组的下标保存对应的属性。如果这时只是需要这堆数据的相对属性，那么可以对其进行离散化处理。当数据只与它们之间的相对大小有关，而与具体是多少无关时，可以进行离散化。
例 1：
91054 与 52143的逆序对个数相同。
例 2：
设有4个数： 1234567、123456789、12345678、123456
排序：123456<1234567<12345678<123456789
=>1<2<3<4
那么这4个数可以表示成：2、4、3、1
例 3：
比如给你n个数：98998988,32434234,433234556,32434234,8384733,……
让你统计其中每个数出现的次数，传统的做法有好几种，比如一遍一遍的扫过去，比对叠加，这样算法的效率是O(n2)，效率低下；
再比如先排序，再统计连续的相同的个数，这里的效率已经有所提高了，不过假如上面的数据是一道线段树的题目给出的数据，那么建树需要的空间开销实在是太大了。
再改进一下，采用哈希的方法，开一个大于其中最大数的数组并初始化为零，O(n)扫一下，在该数字对应的下标的元素上+1，如果对于比较小的数字还好说，但是对于上面出现的数字直接采用哈希对空间的开销是十分大的也是没有必要的，所以这里用到了数据的离散化。
首先将数字排序：32434234，32434234，43324556，8384733，98998988
去重后给予其对应的索引： 0,0,1,2,3 （一一映射）
分别对应每个数，就可以简化很多操作，减少了很多不必要的资源开销。
除了对于较大整数需要使用离散化之外，对于一些需要使用整型数据结构，但给出的数据却是小数的也可以使用离散化，将其索引为整数就可以了。

那么可以总结出离散化的步骤：

1、排序

2、去重

3、索引
为了简化代码，我们采用STL离散化：

1 /*
2 用离散化之前先用 sort（）排序，再用 unique() 进行去重
3 用 lower_bound() 或者 upper_bound() 进行二分查找位置
4 */
5 int a[n], b[n], sub[n];/// a[n]是即将被离散化的数组，b[n]是a[n]的副本，sub用于排序去重后提供离散化后的值
6 sort(sub, sub + n);
7 int size = unique(sub, sub + n) - sub;
8 for(int i = 0; i < n; i++)
9     a[i] = lower_bound(sub, sub + size, a[i]) - sub;///即a[i]为b[i]离散化后对应的值

uinque()函数

头文件

#include<iostream>

unique 的作用是“去掉”容器中相邻元素的重复元素，这里所说的“去掉”并不是真正把重复元素删除，它实质上是一个伪去除，是把重复的元素移到后面去了，然后依然保存到了原数组中，然后返回去重后最后一个元素的地址。
因为unique去除的是相邻元素的重复元素，所以使用之前需要排序。

sz=unique(b+1,b+n+1)-(b+1);//减去的（b+1) 起始地址
sz=unique(a,a+n)-a;

unique(a,a+n) - a返回的是去重后的数组长度

二分查找lower_bound()、upper_bonud()

1、lower_bound函数

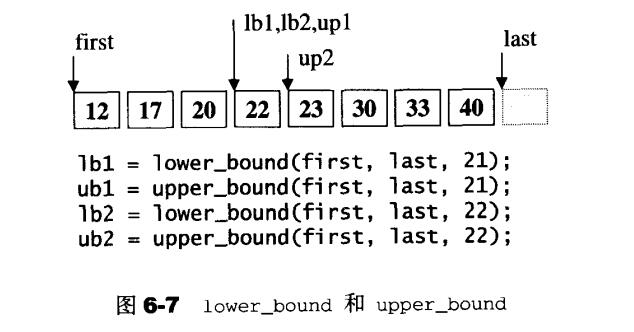
在一个非递减序列的前闭后开区间[first,last)中，进行二分查找查找某一元素val，函数lower_bound()返回大于或等于val的第一个元素位置（即满足条件a[i]>=val(first<=i<last)的最小的i的值），当区间的所有元素都小于val时，函数返回的i值为last（注意：此时i的值是越界的！！！！！）。

STL中函数lower_bound()的代码实现(first是最终要返回的位置)

 1 int lower_bound(int *array, int size, int key)
 2 {
 3     int first = 0, middle, half, len;
 4     len = size;
 5     while(len > 0)
 6     {
 7         half = len >> 1;
 8         middle = first + half;
 9         if(array[middle] < key)
10         {
11             first = middle +1;
12             len = len - half -1;//在右边子序列中查找
13         }
14         else
15             len = half;//在左边子序列（包含middle）中查找
16     }
17 }

2、upper_bound函数

在一个有序序列（升序或者降序）的区间中，进行二分查找某一元素val，函数upper_bound返回一个迭代器指向该区间中最后一个这个元素的下一个位置（简单的说就是返回能够将元素val插入区间的最后一个位置）。

STL中函数upper_bound()的代码实现(first是最终要返回的位置)

 1 int upper_bound(int *array, int size, int key)
 2 {
 3     int first = 0, len = size-1, half, middle;
 4  
 5     while(len > 0)
 6     {
 7         half = len >> 1;
 8         middle = first + half;
 9         if(array[middle] > key)//中位数大于key,在包含last的左半边序列中查找。
10             len = half;
11         else
12         {
13             first = middle + 1;//中位数小于等于key,在右半边序列中查找。
14             len = len - half - 1;
15         }
16     }
17     return first;
18 }