Codeforces Round 310 Div. 1

A. Case of Matryoshkas (2s, 256MB)

题目大意：给定 \(n\) 个大小从 \(1\) 到 \(n\) 的套娃，且只有小的套娃能套在大的套娃里面。初始时套娃已经被套成 \(k\) 部分，每次可以进行以下两个操作之一

• 选择一个不在任何套娃里的套娃 \(i\)，将里面的套娃取出，要求 \(i\) 中原来有套娃
• 选择一个不在任何套娃里的套娃 \(i\)，将一个套娃放入，要求 \(i\) 中原来没有套娃

求将这 \(k\) 部分套娃合并最少需要进行多少次操作。

数据范围：\(n \leq 10^5\)，\(k \leq 10^5\)

简要题解：分析上述两种操作方法易知，套娃 \(x\) 不用被取出当且仅当

• 套娃 \(x\) 在其中一部分中的最里面
• 存在 \(1,2,\cdots,x\) 的套娃依次相套

那么，只要遍历一遍给出的 \(k\) 个部分，即可统计答案。

时空复杂度：\(O(n) - O(n)\)

关键字：找规律，模拟

B. Case of Fugitive (3s, 256MB)

题目大意：有 \(n\) 个岛屿 \([l_i,r_i]\)，满足 \(\forall 1 \leq i < n\) 有 \(r_i < l_{i+1}\)。现在要在每相邻的两个岛屿间放一座桥，桥的起点 \(x\) 和终点 \(y\) 满足 \(l_i \leq x \leq r_i,l_{i+1} \leq y \leq r_{i+1}\)。若已有 \(m\) 座长度分别为 \(a_1,a_2,\cdots,a_m\) 的桥。问是否存在一种满足要求的安排桥的方案。

数据范围：\(n,m \leq 2 \times 10^5\)，\(1 \leq l_i \leq r_1 \leq 10^{18}\)，\(a_i \leq 10^{18}\)

简要题解：注意到岛屿 \(i\) 和岛屿 \(i+1\) 之间的桥的长度 \(L\) 应满足

\[l_{i+1}-r_i \leq L \leq r_{i+1}-l_i\]

那么问题转化为平面上有 \(n-1\) 条线段和 \(m\) 个点，问是否能找到一个线段与点的匹配方案，使得每条线段与一个该线段上的点匹配，其中每个点只允许被匹配一次。这是一个经典问题。先将线段按右端点从小到大排序，依次枚举每条线段 \([l,r]\)，将小于等于 \(r\) 的点均加入 \(set\) 中，然后取走 \(set\) 中所有大于等于 \(l\) 的点中最小的一个。如果不存在这样的点，则无解。

时空复杂度：\(O((n+m)logm) - O(n+m)\)

关键字：贪心，数据结构

C. Case of Chocolate (3s, 256MB)

题目大意：给定一个 \(n \times n\) 的巧克力，初始时已啃掉副对角线右下方的区域。现在有 \(q\) 个操作，每次选择副对角线上的一个位置，向上或向左啃，直到啃到一个已经被啃过的位置或啃到整块巧克力的边界为止。求每次能啃掉多少个位置的巧克力。

数据范围：\(1 \leq n \leq 10^9\)，\(1 \leq q \leq 2 \times 10^5\)

简要题解：可以把每块巧克力描述为 \((l,r,U,L)\)，其中 \(l\) 和 \(r\) 表示其在副对角线上所处的区间，\(U\) 表示其上边界，\(L\) 表示其左边界。如果把每块巧克力都存在一个 \(set\) 中，那么对于每次操作，可以快速找出其在哪块巧克力上进行，从而得出答案。注意到每次操作最多将一块巧克力变为两块新的巧克力，故复杂度是允许的。题解中提供了一种利用线段树的做法，稍显复杂，但可以借鉴。

时空复杂度：\(O(qlogq) - O(q)\)

关键字：杂题，数据结构

D. Case of a Top Secret (2s, 256MB)

题目大意：给定 \(n\) 个挂点 \(x_1,x_2,\cdots,x_n\) 和 \(m\) 个重物，重物和重物之间不互相影响。第 \(i\) 个重物挂在第 \(a_i\) 个挂点上，挂绳长度为 \(l_i\)，初始时向右摆动，碰到阻碍其的挂点将会转折，如图

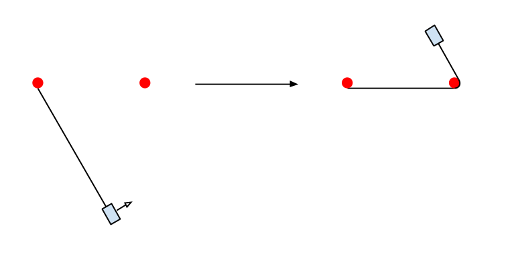
问各个重物将会停在第几个挂点上。

数据范围：\(n,m \leq 2 \times 10^5\)，\(|x_i| \leq 10^9\)，\(1 \leq l_i \leq 10^9\)

简要题解：一个简单的模拟方法是每次二分出下一个阻碍到其摆动的挂点位置，直到其静止。但记录下每次转折的位置后，观察发现

• 如果最后三次转折位置为 \(i \rightarrow i \rightarrow i\)，那么说明 \(i\) 即为答案
• 如果最后三次转折位置为 \(i \rightarrow j \rightarrow i\)，那么说明重物将一直在 \(i,j\) 间来回摆动，直到挂绳不够长，此时取模即可

利用以上两个规律可优化模拟过程，易知只需进行 \(logl_i\) 次模拟即可得到答案。

时空复杂度：\(O(m \cdot logl_i \cdot logn) - O(n)\)

关键字：找规律，二分

E. Case of Computer Network (3s, 256MB)

题目大意：给定一个包含 \(n\) 个点和 \(m\) 条边的无向图和 \(q\) 个要求 \((s_i,d_i)\)。问是否可以将无向图的边定向，使得 \(\forall i \in [1,q]\)，存在一条从 \(s_i\) 到 \(d_i\) 的有向路径。保证图中没有自环，但可以有重边。

数据范围：\(1 \leq n,m,q \leq 2 \times 10^5\)，\(s_i \not= d_i\)

简要题解：注意到一个简单的事实，对于一个无向图中的双联通分量，总存在一种将边重定向的方法，使其转化为有向图中的强联通分量。故先求出该图中的双联通分量并缩点，则原图转化为森林。考虑其中一棵树，若原问题答案为否，则存在一个结点 \(x\) 和两个要求 \((s_i,d_i),(s_j,d_j)\) ，满足 \(s_i,d_j\) 为子树 \(x\) 中的节点且 \(d_i,s_j\) 为子树 \(x\) 外的节点。那么只要判断是否存在上述情况即可。先求出树的 \(DFS\) 序，则一棵子树对应序列中的一段区间 \([l,r]\)。令

\[A=\{s_i|d_i \in [l,r]\},B=\{d_i|s_i \in [l,r]\}\]

则只要检验 \(A,B\) 集合中的最大值和最小值是否在区间 \([l,r]\) 外即可。

时空复杂度：\(O(n+nlogn+q) - O(nlogn)\)

关键字：图论，双联通分量，ST表

转载于:https://www.cnblogs.com/lijingze8/p/6485814.html