【机器学习基础】对 softmax 和 cross-entropy 求导

在论文中看到对 softmax 和 cross-entropy 的求导，一脸懵逼，故来整理整理。

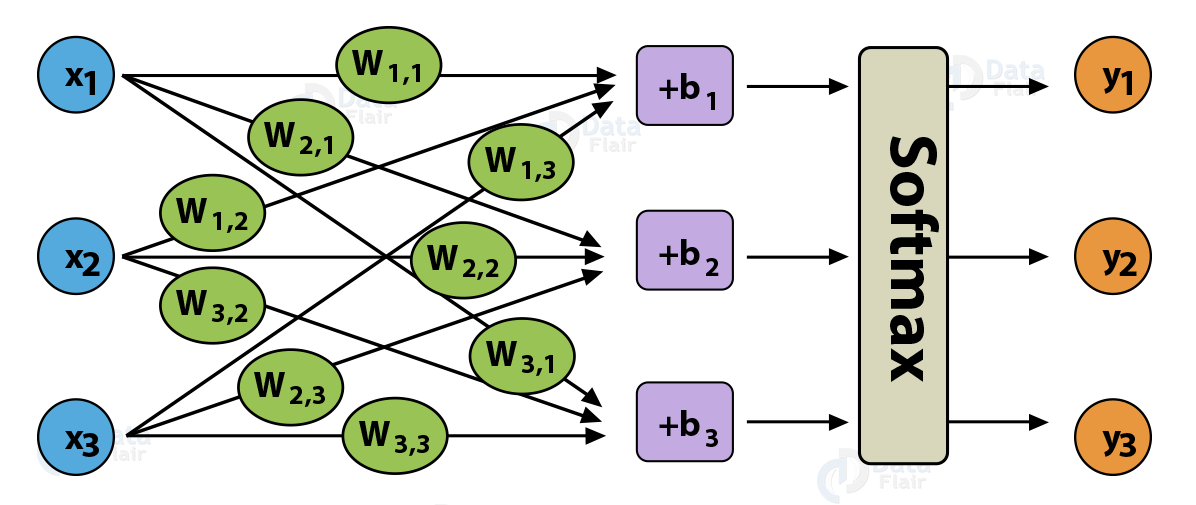
以 softmax regression 为例来展示求导过程，softmax regression 可以看成一个不含隐含层的多分类神经网络，如 Fig. 1 所示。

Fig. 1 Softmax Regression.

softmax regression 的矩阵形式如 Fig. 2 所示：

Fig. 2 Matrix Form.

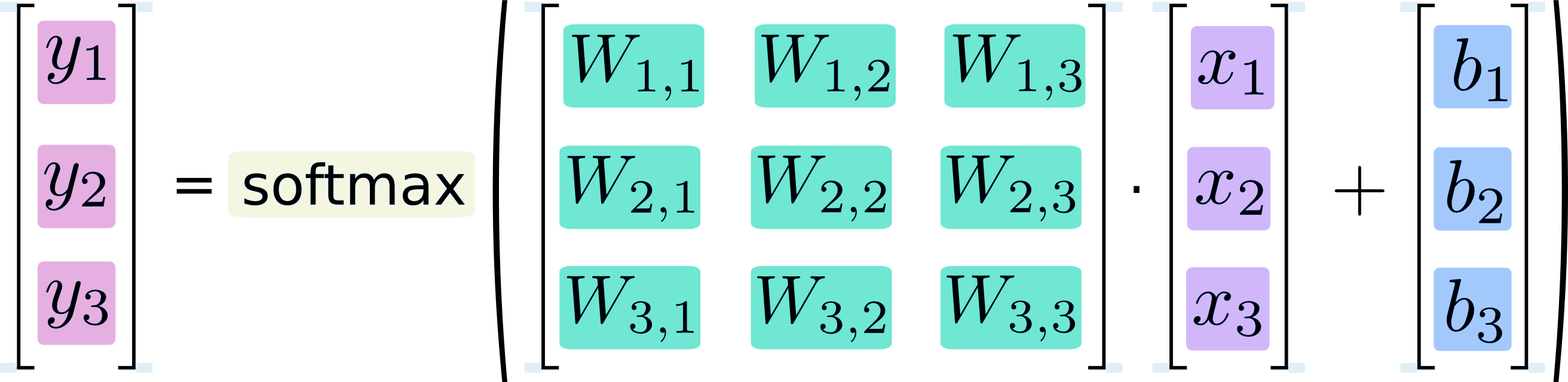
符号定义

如 Fig. 1 所示，\(\bm x = [x_1, x_2, x_3]^{\top}\) 表示 softmax regression 的输入，\(\bm y = [y_1, y_2, y_3]^{\top}\) 表示 softmax regression 的输出，\(\bm W\) 为权重，\(\bm b = [b_1, b_2, b_3]^{\top}\) 为偏置。

令 Fig. 2 中 softmax function 的输入为 \(z_i = W_{i, 1}x_1 + W_{i, 2}x_2 + W_{i, 3}x_3 + b_i = W_{i}\bm x + b_i\)，其中 \(i= 1, 2, 3\)，\(W_{i}\) 表示权重矩阵 \(\bm W\) 的第 \(i\) 行；softmax function 的输出就是整个网络的输出，即 \(\bm y\)。

Note: Fig. 1 和 Fig.2 中权重 \(W_{i, j}\) 表示第 \(i\) 个输出和第 \(j\) 个输入之间的联系，和一般的记法（即 \(W_{i, j}\) 表示第 \(i\) 个输入和第 \(j\) 个输出之间权重）相差一个转置。

用 \(m\) 表示输出的类别数，本文中 \(m = 3\)。

Note: softmax regression 指的是整个网络，softmax function 仅仅指的是激活函数。本文默认 softmax 代指激活函数，当表示整个网络时会明确说明 softmax regression。

对 softmax 求导

softmax 函数的表达式为：
\[ y_i = \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}} \tag{1} \]

其中 \(i= 1, 2, 3\)。由式（1）可知，\(y_i\) 与 softmax function 所有的输入 \(z_j, j = 1,2,3.\) 都有关。
softmax function 的输出对其输入求偏导：
\[ \frac{\partial y_i}{\partial z_j} = \frac{\partial \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}}}{\partial z_j} \tag{2} \]

需要对式（2）中 \(i = j\) 和 \(i \not = j\) 的情况进行分别讨论。因为式（1）分子中仅含第 \(i\) 项，式（2）中如果 \(i = j\)，那么导数 \(\frac{\partial e^{z_i}}{\partial z_j} = e^{z_i}\)，不为 0；如果 \(i \not = j\)，那导数 \(\frac{\partial e^{z_i}}{\partial z_j} = 0\)。

• \(i = j\)，则式（2）为：
  \[ \begin{split} \frac{\partial y_i}{\partial z_j} &= \frac{\partial \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}}}{\partial z_j} \\ &= \frac{e^{z_i} \cdot \sum_{t = 1}^m e^{z_t} - e^{z_i} \cdot e^{z_j} }{(\sum_{t = 1}^m e^{z_t})^2} \\ &= \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}} - \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}} \cdot \frac{e^{z_j}}{\sum_{t = 1}^m e^{z_t}} \\ &=y_i(1 - y_j) \end{split} \tag{3} \]

当然，式（3）也可以写成 \(y_i(1 - y_i)\) 或者 \(y_j(1 - y_j)\)，因为这里 \(i = j\)。

• \(i \not = j\)，则式（2）为：
  \[ \begin{split} \frac{\partial y_i}{\partial z_j} &= \frac{\partial \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}}}{\partial z_j} \\ &= \frac{0\cdot \sum_{t = 1}^m e^{z_t} - e^{z_i} \cdot e^{z_j} }{(\sum_{t = 1}^m e^{z_t})^2} \\ &= - \frac{e^{z_i}}{\sum_{t = 1}^m e^{z_t}} \cdot \frac{e^{z_j}}{\sum_{t = 1}^m e^{z_t}} \\ &= -y_iy_j \end{split} \tag{4} \]

对 cross-entropy 求导

令 \(\bm {\hat y} = [\hat{y}_1, \hat{y}_2, \hat{y}_3]^{\top}\) 为输入 \(\bm x\) 真实类别的 one-hot encoding。

cross entropy 的定义如下：
\[ H(\bm {\hat y}, \bm y) = - \bm {\hat y}^{\top} \log \bm y = - \sum_{t = 1}^m \hat{y}_t\log y_t \tag{5} \]

对 cross entropy 求偏导：（\(\log\) 底数为 \(e\)）
\[ \frac{\partial H(\bm {\hat y}, \bm y) }{\partial y_i} = \frac{\partial [- \sum_{t = 1}^m \hat{y}_t\log y_t ]}{\partial y_i} = - \frac{\hat{y}_i}{y_i} \tag{6} \]

\(\bm {\hat y}\) 是确定的值，可以理解为样本的真实 one-hot 标签，不受模型预测标签 \(\bm y\) 的影响。

对 softmax 和 cross-entropy 一起求导

\[ \begin{split} \frac{\partial H(\bm {\hat y}, \bm y) }{\partial z_j} &= \sum_{i = 1}^{m} \frac{\partial H(\bm {\hat y}, \bm y) }{\partial y_i} \frac{\partial y_i }{\partial z_j} \\ &= \sum_{i = 1}^{m} -\frac{\hat{y}_i}{y_i} \cdot \frac{\partial y_i }{\partial z_j} \\ &= \left(-\frac{\hat{y}_i}{y_i} \cdot \frac{\partial y_i }{\partial z_j}\right )_{i = j} + \sum_{i = 1 , i \not = j}^{m} -\frac{\hat{y}_i}{y_i} \cdot \frac{\partial y_i }{\partial z_j} \\ &= -\frac{\hat{y}_j}{y_i} \cdot y_i(1-y_j) + \sum_{i = 1 , i \not = j}^{m} -\frac{\hat{y}_i}{y_i} \cdot -y_iy_j \\ &= - \hat{y}_j + \hat{y}_jy_j + \sum_{i = 1 , i \not = j}^{m} \hat{y}_iy_j \\ & = - \hat{y}_j + y_j\sum_{i = 1}^{m} \hat{y}_i \\ &= y_j - \hat{y}_j \end{split} \tag{7} \]

交叉熵 loss function 对 softmax function 输入 \(z_j\) 的求导结果相当简单，在 tensorflow 中，softmax 和 cross entropy 也合并成了一个函数，tf.nn.softmax_cross_entropy_with_logits，从导数求解方面看，也是有道理的。

在实际使用时，推荐使用 tensorflow 中实现的 API 去实现 softmax 和 cross entropy，而不是自己写，原因如下：

• 都已经有 API 了，干嘛还得自己写，懒就是最好的理由；
• softmax 因为计算了 exp(x)，很容易就溢出了，比如 np.exp(800) = inf，需要做一些缩放，而 tensorflow 会帮我们处理这种数值不稳定的问题。

References

TensorFlow MNIST Dataset and Softmax Regression - Data Flair
链式法则 - 维基百科
Softmax函数与交叉熵 - 知乎

转载于:https://www.cnblogs.com/wuliytTaotao/p/10787510.html