Positive-definite matrix

最新推荐文章于 2024-11-28 23:55:01 发布

转载最新推荐文章于 2024-11-28 23:55:01 发布 · 186 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/hanhuilee/p/5221270.html

本文介绍了线性代数中正定矩阵的概念，详细解释了实对称矩阵和埃尔米特矩阵成为正定矩阵的条件，并通过具体的例子展示了如何判断一个矩阵是否为正定矩阵。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

In linear algebra, a symmetric n × n real matrix M is said to be positive definite if z^TMz is positive for every non-zero columnvector z of n real numbers. Here z^T denotes thetranspose of z.

The real symmetric matrix

M = \begin{bmatrix} 2&-1&0\\-1&2&-1\\0&-1&2 \end{bmatrix}

is positive definite since for any non-zero column vector z with entries a, b and c, we have

\begin{align} z^{\mathrm{T}}M z = (z^{\mathrm{T}}M) z &= \begin{bmatrix} (2a-b)&(-a+2b-c)&(-b+2c) \end{bmatrix} \begin{bmatrix} a\\b\\c \end{bmatrix} \\&= 2{a}^2 - 2ab + 2{b}^2 - 2bc + 2{c}^2 \\&= {a}^2+(a - b)^{2} + (b - c)^{2}+{c}^2\end{align}

This result is a sum of squares, and therefore non-negative; and is zero only if a = b = c = 0, that is, when z is zero.

The real symmetric matrix

N = \begin{bmatrix} 1 & 2 \\ 2 & 1\end{bmatrix}

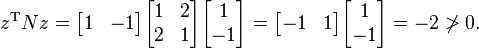
is not positive definite. If z is the vector $\begin{bmatrix} 1\\ -1\end{bmatrix}$ , one has $z^{\mathrm{T}}N z = \begin{bmatrix} 1 & -1\end{bmatrix} \begin{bmatrix} 1 & 2 \\ 2 & 1\end{bmatrix} \begin{bmatrix} 1 \\ -1\end{bmatrix}=\begin{bmatrix} -1 & 1\end{bmatrix} \begin{bmatrix} 1 \\ -1\end{bmatrix}=-2 \not > 0.$

More generally, an n × n Hermitian matrix M is said to be positive definite if z*Mz is real and positive for all non-zero complex vectors z. Here z* denotes the conjugate transpose of z.

摘自：https://en.wikipedia.org/wiki/Positive_semidefinite_matrix

转载于:https://www.cnblogs.com/hanhuilee/p/5221270.html

确定要放弃本次机会？

福利倒计时

: :

立减 ¥

普通VIP年卡可用

立即使用

weixin_30457551

关注关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
分享

复制链接

分享到 QQ

分享到新浪微博

扫一扫
举报

举报

正定矩阵（Positive Definite Matrices）、半正定矩阵（Positive Semidefinite Matrices）

一个搬运知识的笨小孩

01-29

1万+

正定矩阵、半正定矩阵1.正定矩阵、半正定矩阵1.1 正定矩阵1.1.1 判断正定矩阵1.2 半正定矩阵1.2.1 判定半正定矩阵1.3 椭圆 ax2+2bxy+cy2=1ax^2+2bxy+cy^2=1ax2+2bxy+cy2=11.3.1 与对称矩阵SSS有关的椭圆1.3.2 与特征值矩阵Λ\LambdaΛ有关的椭圆1.4 重要应用：检验最小值 1.正定矩阵、半正定矩阵 1.1 正定矩阵 1.1.1 判断正定矩阵 1.矩阵的所有特征值都为正数下面以对称矩阵为例，对称矩阵的特征值为正数，所以对称矩阵是

正定矩阵(Positive-definite Matrix)

無名黑洞

08-14

2万+

正定矩阵式自共轭矩阵的一种。正定矩阵类似复数中的正实数。定义：对于对称矩阵M，当且仅当存在任意向量x，都有若上式大于等于零，则称M为半正定矩阵。正定矩阵记为M>0。也被称为正定二次型正定矩阵的判定 1、所有特征值为正数（根据谱定理，若条件成立，必然可以找到对角矩阵呢D和正定矩阵P，使M=P^-1DP）； 2、所有的顺序主子式为正定； 3、Cholesky分解得到的

参与评论您还未登录，请先登录后发表或查看评论

正定矩阵（Positive Definite Matrix）

二分掌柜的

06-20

7132

flyfish

positive definite matrix

weixin_40493805的博客

02-18

406

1、有些概念是躲不过的，那就面对吧。先收藏一个没有相关的资源 https://www.geogebra.org 2、先参考别人的解释，还是很有道理的。参考 https://blog.youkuaiyun.com/qq_24753293/article/details/80014403 这个里面有很多引用其他人的解释，这里先收藏一下。 3、自己的总结还是要有的。首先定义：主要是这个matrix是针对any...

【线性代数】6-5:正定矩阵(Positive Definite Matrices)

Tony的博客

09-22

9721

title: 【线性代数】6-5:正定矩阵(Positive Definite Matrices) categories: Mathematic Linear Algebra keywords: Positive Definite Matrices Symmetric Matrices Eigenvalues Eigenvectors toc: true date: 2017-11-24 11...

正定矩阵 Positive definite matrix

Jason Leaster | Rebuilding the tower of babel

11-16

4786

Positive definite matrix

Positive Semi-definite matrix

家家的专栏

11-11

6609

Definition: A real symmetric m*m matrix K satisfying for all (m-dimisionational vector a) is called a positive semi-definite matrix. Theorems: (1) A real symmetric matrix is diagonaliza

矩阵理论| 特殊矩阵：正定矩阵

Insomnia_X的博客

02-13

7434

一方面因为实对称正定矩阵拥有良好性质，另一个原因是实对称正定矩阵的分析就足以应付其他一般的正定矩阵（原理：任何矩阵。

正定矩阵（Positive Definite Matrix）的定义与性质

最新发布

小黄人的博客

11-28

4540

一个n×nn \times nn×n的实对称矩阵AAA是正定矩阵，当且仅当它满足以下等价条件之一：对任意非零向量x∈Rnx∈RnxTAx0xTAx0矩阵的所有特征值均为正。存在一个满秩矩阵BBB，使得ABTBA = B^T BABTB（针对复矩阵）AAA是 Hermitian 矩阵（共轭对称矩阵），且所有特征值均为正。对于复矩阵AAA，如果满足xHAx0xHAx0（其中xHx^HxH表示。

Positive Semidefinite Matrix

nipirennipi136的博客

05-14

2495

半正定矩阵（Positive Semidefinite Matrix）半正定二次型定义：设二次型 xTAx\boldsymbol{x^T}A\boldsymbol{x}xTAx，若对任意 x≠0\boldsymbol{x} \neq \boldsymbol{0}x=0，都有 f(x)⩾0f(\boldsymbol{x})\geqslant0f(x)⩾0，则称 fff 为半正定二次型。半正定矩阵定义：设实对称矩阵 AAA，若对任意 x≠0\boldsymbol{x} \neq \bol

核函数矩阵为什么要是positive semidefinite的

weixin_33727510的博客

11-17

580

《支持向量机导论》中证明核函数矩阵$\mathbf{K}=(K(\mathbf{x}_{i},\mathbf{x}_{j}))_{i,j=1}^{n}$必须是半正定矩阵的方法是用的反证法，构造了一个反例，\[\mathbf{z}=\sum_{i=1}^{n}v_{si}\mathbf{\mathbf{\Phi}}(\mathbf{x}_{i})=\sqrt{\Lambda}V'v_{s}\]这...

半正定矩阵

weixin_49342084的博客

10-29

4520

虽然半正定矩阵是对称的，但如果我们考虑复数域上的Hermitian矩阵（共轭对称矩阵），其谱分解依然成立，只是U变成了酉矩阵。对于半正定矩阵，如果最小特征值为零，则条件数为无穷大，表示该矩阵是奇异的。半正定矩阵 (Positive Semidefinite Matrix) 是线性代数和矩阵分析中的一个重要概念，它描述了一类特殊的对称矩阵。这种凸性使得半正定矩阵在凸优化中扮演着重要的角色，因为许多涉及半正定矩阵的优化问题都是凸优化问题，从而保证了全局最优解的存在性和可求解性。这是判断半正定矩阵最常用的方法。

r语言中正定矩阵由于误差不正定_矩阵的几种分解方式 - 加强版

weixin_39620279的博客

10-19

765

虽然之前写过一篇，但是回首再来看发现有很多地方其实可以总结的更清楚，所以再写一个加强版。在开始之前先补充一些定义。定义共轭转置 Conjugate transpose如果我们有一个复数矩阵A：它的转置：共轭转置 : 共轭转置也经常记为：（这个写法跟下面的 Hermitian 定义有关）, HermitianHermitian matrix 埃尔米特矩阵：埃尔米特矩阵中每一个第i...

正定矩阵的意义

po5889的专栏

08-30

1万+

正定矩阵的定义（引自百度百科）设M是n阶实系数对称矩阵，如果对任何一非零实向量X，都使二次型f(X)= X′MX>0，则称f（X）为正定二次型，f(X)的矩阵M称为正定矩阵(Positive Definite)。　正定矩阵在相合变换下可化为标准型，即单位矩阵。所有特征值大于零的对称矩阵（或厄米特矩阵）也是正定矩阵。另一种定义：一种实对称矩阵.正定二次型f(x1,x2,…

正定矩阵（positive definite matrix）

03-14

2457

为什么要研究正定矩阵？矩阵分解——三角分解（Cholesky 分解）因为正定矩阵有一些美好的性质，比如存在唯一的 LDULDU 分解，如果为实对称的话，可进一步分解为 GGTGG^T，而矩阵的三角分解带来的的巨大的计算复杂度的下降。而样本的协方差矩阵正是一种实对称正定矩阵。

矩阵分解 Cholesky分解

billbliss的专栏

11-17

3万+

Cholesky分解法又叫平方根法，是求解对称正定线性方程组最常用的方法之一。对于一般矩阵，为了消除LU分解的局限性和误差的过分积累，采用了选主元的方法，但对于对称正定矩阵而言，选主元是不必要的。定理：若对称正定，则存在一个对角元为正数的下三角矩阵，使得成立。假设现在要求解线性方程组，其中为对称正定矩阵，那么可通过下面步骤求解（1）求的

Positive-definite matrix（正定矩阵）

zhrh0096的专栏

04-14

2561

正定矩阵定义 In linear algebra, a symmetric(对称) n × n real matrix M is said to be positive definite if zTMz is positive, for any non-zero column vector z of n real numbers; where zT denotes the trans

线性代数笔记11：正定矩阵理解及推导