图论

---

Some Definations.

DFST: 深度优先生成树

二分图

1. 若一个图不存在奇环，那么这是二分图。（二分图中的环只能是偶环，无奇环）

竞赛图

竞赛图：每对顶点之间都有一条(有向)边相连的有向图。
性质：
1. 竞赛图一定存在哈密顿通路，强连通竞赛图一定存在哈密顿回路。

大致证明(数学归纳)：
　　首先三个点时显然。假设现在有1->2->3->...，存在一条哈密顿通路。加入一个点n，无论其它点与n的边怎么连，都能形成哈密顿通路。回路同理。

2. \((i,n\geq 3\ ,\ i\leq n)\) n个点的强连通竞赛图中包含有长度为i的简单环。

大致证明(数学归纳)：
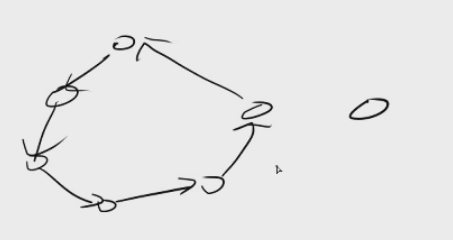
　　假设现在有左边n个点的强连通竞赛图，考虑新加入的点x，

　　假如这条边是这样的(由x连向原图点j)：

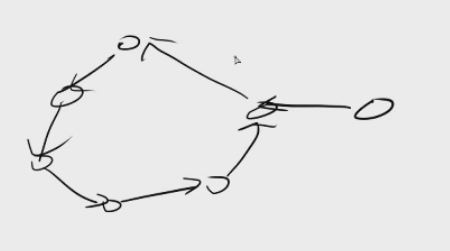
　　如果要不产生环，那么x与第二个点i的连边只能是x->i，否则就产生了i->x->j 成了一个环。
　　同理对于每个点都只能这么取。
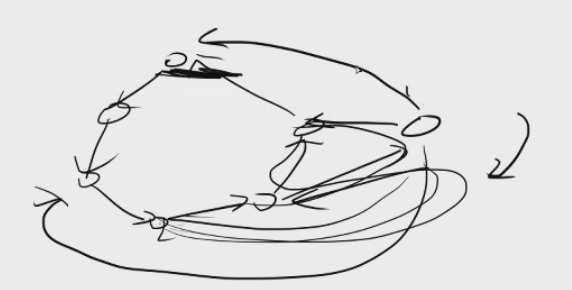
　　到最后一个点时，如果还这么取，

　　我们可以发现，图变得不是强连通图了。所以不可能这样取边。

3. 竞赛图缩点后一定是条链。

大致证明：
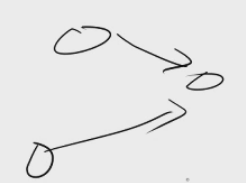
　　假如缩点后不是一条链，是这样的话：

　　左边这两个点肯定有条边，

　　要么会把这条边删去：

　　要么会把另一条删去：

转载于:https://www.cnblogs.com/SovietPower/p/8461802.html