Dancing Links

Dancing Links

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In computer science, Dancing Links, also known as DLX, is the technique suggested by Donald Knuth to efficiently implement his Algorithm X^[1]. Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem. Some of the better-known exact cover problems include tiling, the N queens problem, and Sudoku.

The name Dancing Links comes from the way the algorithm works, as iterations of the algorithm cause the links to "dance" with partner links so as to resemble an "exquisitely choreographed dance." Knuth credits Hirosi Hitotumatu and Kohei Noshita with having invented the idea in 1979,^[2] but it is his paper which has popularized it.

[edit] Implementation

As the remainder of this article discusses the details of an implementation technique for Algorithm X, the reader is strongly encouraged to read the Algorithm X article first.

[edit] Main ideas

The idea of DLX is based on the observation that in a circular doubly linked list of nodes,

x.left.right ← x.right;x.right.left ← x.left;

will remove node x from the list, while

x.left.right ← x;x.right.left ← x;

will restore x's position in the list. This works regardless of the number of elements in the list, even if that number is 1.

Knuth observed that a naive implementation of his Algorithm X would spend an inordinate amount of time searching for 1's. When selecting a column, the entire matrix had to be searched for 1's. When selecting a row, an entire column had to be searched for 1's. After selecting a row, that row and a number of columns had to be searched for 1's. To improve this search time from complexity O(n) to O(1), Knuth implemented a sparse matrix where only 1's are stored.

At all times, each node in the matrix will point to the adjacent nodes to the left and right (1's in the same row), above and below (1's in the same column), and the header for its column (described below). Each row and column in the matrix will consist of a circular doubly linked list of nodes.

[edit] Header

Each column will have a special node known as the "column header," which will be included in the column list, and will form a special row ("control row") consisting of all the columns which still exist in the matrix.

Finally, each column header may optionally track the number of nodes in its column, so that locating a column with the lowest number of nodes is of complexity O(n) rather than O(n×m) where n is the number of columns and m is the number of rows.

[edit] Exploring

In Algorithm X, rows and columns are regularly eliminated from and restored to the matrix. Eliminations are determined by selecting a column and a row in that column. If a selected column doesn't have any rows, the current matrix is unsolvable and must be backtracked. When an elimination occurs, the selected row's column, other rows 'belonging' to that column, and other columns to which the selected row 'belongs' are all removed. These columns are removed because they have been filled, and these rows are removed because they conflict with the selected row. To perform the elimination, first remove the selected column's header. Next, for each row where the selected column contains a 1, traverse the row and remove it from other columns (this makes those rows inaccessible and is how conflicts are prevented). Finally, remove each column (other than the selected column, it has already been removed) in which the selected row has a 1 (they have been filled by the selected row). This order ensures that any removed node is removed exactly once and in a predictable order, so it can be backtracked appropriately. If the resulting matrix has no columns, then they have all been filled and the selected rows form the solution.

[edit] Backtracking

To backtrack, the above process must be reversed using the second algorithm stated above. One requirement of using that algorithm is that backtracking must be done as an exact reversal of eliminations. Knuth's paper gives a clear picture of these relationships and how the node removal and reinsertion works, and provides a slight relaxation of this limitation.

[edit] Optional constraints

It is also possible to solve one-cover problems in which a particular constraint is optional, but can be satisfied no more than once. Dancing Links accommodates these with primary columns which must be filled and secondary columns which are optional. This alters the algorithm's solution test from a matrix having no columns to a matrix having no primary columns, but doesn't require any further changes. Knuth discusses optional constraints as applied to the N queens problem. The chessboard diagonals represent optional constraints, as some diagonals may not be occupied. If a diagonal is occupied, it can only be occupied only once.

Knuth's Algorithm X

From Wikipedia, the free encyclopedia

  (Redirected from Algorithm X)

Jump to: navigation, search

Donald Knuth's Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem represented by a matrix A consisting of 0s and 1s. The goal is to select a subset of the rows so that the digit 1 appears in each column exactly once.

Algorithm X functions as follows:

If the matrix A is empty, the problem is solved; terminate successfully. Otherwise choose a column c (deterministically). Choose a row r such that Ar, c = 1 (nondeterministically). Include row r in the partial solution. For each column j such that Ar, j = 1, for each row i such that A i, j = 1, delete row i from matrix A; delete column j from matrix A.

Repeat this algorithm recursively on the reduced matrix A.

The nondeterministic choice of r means that the algorithm essentially clones itself into independent subalgorithms; each subalgorithm inherits the current matrix A, but reduces it with respect to a different row r. If column c is entirely zero, there are no subalgorithms and the process terminates unsuccessfully.

The subalgorithms form a search tree in a natural way, with the original problem at the root and with level k containing each subalgorithm that corresponds to k chosen rows. Backtracking is the process of traversing the tree in preorder, depth first.

Any systematic rule for choosing column c in this procedure will find all solutions, but some rules work much better than others. To reduce the number of iterations, Knuth suggests that the column choosing algorithm select a column with the lowest number of 1s in it.

[edit] Example

For example, consider the exact cover problem specified by the universe U = {1, 2, 3, 4, 5, 6, 7} and the collection of sets 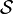= {A, B, C, D, E, F}, where:

• A = {1, 4, 7};
• B = {1, 4};
• C = {4, 5, 7};
• D = {3, 5, 6};
• E = {2, 3, 6, 7}; and
• F = {2, 7}.

This problem is represented by the matrix:

	1	2	3	4	5	6	7
A	1	0	0	1	0	0	1
B	1	0	0	1	0	0	0
C	0	0	0	1	1	0	1
D	0	0	1	0	1	1	0
E	0	1	1	0	0	1	1
F	0	1	0	0	0	0	1

Algorithm X with Knuth's suggested heuristic for selecting columns solves this problem as follows:

Level 0

Step 1—The matrix is not empty, so the algorithm proceeds.

Step 2—The lowest number of 1s in any column is two. Column 1 is the first column with two 1s and thus is selected (deterministically):

	1	2	3	4	5	6	7
A	1	0	0	1	0	0	1
B	1	0	0	1	0	0	0
C	0	0	0	1	1	0	1
D	0	0	1	0	1	1	0
E	0	1	1	0	0	1	1
F	0	1	0	0	0	0	1

Step 3—Rows A and B each have a 1 in column 1 and thus are selected (nondeterministically).

The algorithm moves to the first branch at level 1…

Level 1: Select Row A

Step 4—Row A is included in the partial solution.

Step 5—Row A has a 1 in columns 1, 4, and 7:

	1	2	3	4	5	6	7
A	1	0	0	1	0	0	1
B	1	0	0	1	0	0	0
C	0	0	0	1	1	0	1
D	0	0	1	0	1	1	0
E	0	1	1	0	0	1	1
F	0	1	0	0	0	0	1

Column 1 has a 1 in rows A and B; column 4 has a 1 in rows A, B, and C; and column 7 has a 1 in rows A, C, E, and F. Thus rows A, B, C, E, and F are to be removed and columns 1, 4 and 7 are to be removed:

	1	2	3	4	5	6	7
A	1	0	0	1	0	0	1
B	1	0	0	1	0	0	0
C	0	0	0	1	1	0	1
D	0	0	1	0	1	1	0
E	0	1	1	0	0	1	1
F	0	1	0	0	0	0	1

Row D remains and columns 2, 3, 5, and 6 remain:

	2	3	5	6
D	0	1	1	1

Step 1—The matrix is not empty, so the algorithm proceeds.

Step 2—The lowest number of 1s in any column is zero and column 2 is the first column with zero 1s:

	2	3	5	6
D	0	1	1	1

Thus this branch of the algorithm terminates unsuccessfully.

The algorithm moves to the next branch at level 1…

Level 1: Select Row B

Step 4—Row B is included in the partial solution.

Row B has a 1 in columns 1 and 4:

	1	2	3	4	5	6	7
A	1	0	0	1	0	0	1
B	1	0	0	1	0	0	0
C	0	0	0	1	1	0	1
D	0	0	1	0	1	1	0
E	0	1	1	0	0	1	1
F	0	1	0	0	0	0	1

Column 1 has a 1 in rows A and B; and column 4 has a 1 in rows A, B, and C. Thus rows A, B, and C are to be removed and columns 1 and 4 are to be removed:

	1	2	3	4	5	6	7
A	1	0	0	1	0	0	1
B	1	0	0	1	0	0	0
C	0	0	0	1	1	0	1
D	0	0	1	0	1	1	0
E	0	1	1	0	0	1	1
F	0	1	0	0	0	0	1

Rows D, E, and F remain and columns 2, 3, 5, 6, and 7 remain:

	2	3	5	6	7
D	0	1	1	1	0
E	1	1	0	1	1
F	1	0	0	0	1

Step 1—The matrix is not empty, so the algorithm proceeds.

Step 2—The lowest number of 1s in any column is one. Column 5 is the first column with one 1 and thus is selected (deterministically):

	2	3	5	6	7
D	0	1	1	1	0
E	1	1	0	1	1
F	1	0	0	0	1

Step 3—Row D has a 1 in column 5 and thus is selected (nondeterministically).

The algorithm moves to the first branch at level 2…

Level 2: Select Row D

Step 4—Row D is included in the partial solution.

Step 5—Row D has a 1 in columns 3, 5, and 6:

	2	3	5	6	7
D	0	1	1	1	0
E	1	1	0	1	1
F	1	0	0	0	1

Column 3 has a 1 in rows D and E; column 5 has a 1 in row D; and column 6 has a 1 in rows D and E. Thus rows D and E are to be removed and columns 3, 5, and 6 are to be removed:

	2	3	5	6	7
D	0	1	1	1	0
E	1	1	0	1	1
F	1	0	0	0	1

Row F remains and columns 2 and 7 remain:

	2	7
F	1	1

Step 1—The matrix is not empty, so the algorithm proceeds.

Step 2—The lowest number of 1s in any column is one. Column 2 is the first column with one 1 and thus is selected (deterministically).

Row F has a 1 in column 2 and thus is selected (nondeterministically).

The algorithm moves to the first branch at level 3…

Level 3: Select Row F

Step 4—Row F is included in the partial solution.

Row F has a 1 in columns 2 and 7:

	2	7
F	1	1

Column 2 has a 1 in row F; and column 7 has a 1 in row F. Thus row F is to be removed and columns 2 and 7 are to be removed:

	2	7
F	1	1

Step 1—The matrix is empty, thus this branch of the algorithm terminates successfully.

As rows B, D, and F are selected, the final solution is:

	1	2	3	4	5	6	7
B	1	0	0	1	0	0	0
D	0	0	1	0	1	1	0
F	0	1	0	0	0	0	1

In other words, the subcollection { B, D, F} is an exact cover, since every element is contained in exactly one of the sets B = {1, 4}, D = {3, 5, 6}, or F = {2, 7}.

There are no more selected rows at level 3, thus the algorithm moves to the next branch at level 2…

There are no more selected rows at level 2, thus the algorithm moves to the next branch at level 1…

There are no more selected rows at level 1, thus the algorithm moves to the next branch at level 0…

There are no branches at level 0, thus the algorithm terminates.

In summary, the algorithm determines there is only one exact cover: = {B, D, F}.

转载于:https://www.cnblogs.com/waterfalleagle/archive/2010/12/11/1902865.html