



注意仿射包中的集合C1与放松集中的C2不是指同一个,仿射包中的C1指的是线段、三角形、球体
仿射集中的C2值直线、平面、超平面。C1的仿射包就是仿射集C2


内点就是集合内一开始就存在于边界内部的点,相对内点是后来拿出来一个点,判断出它在集合内的点
x=Θx1+(1-Θ)x2表示x1到x2之间的点

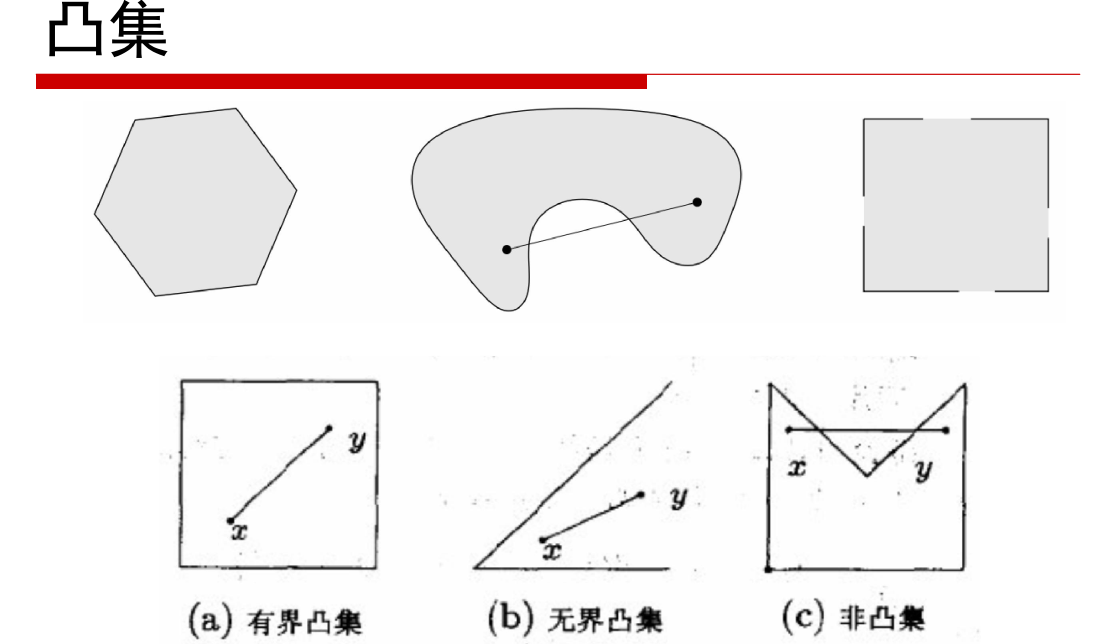
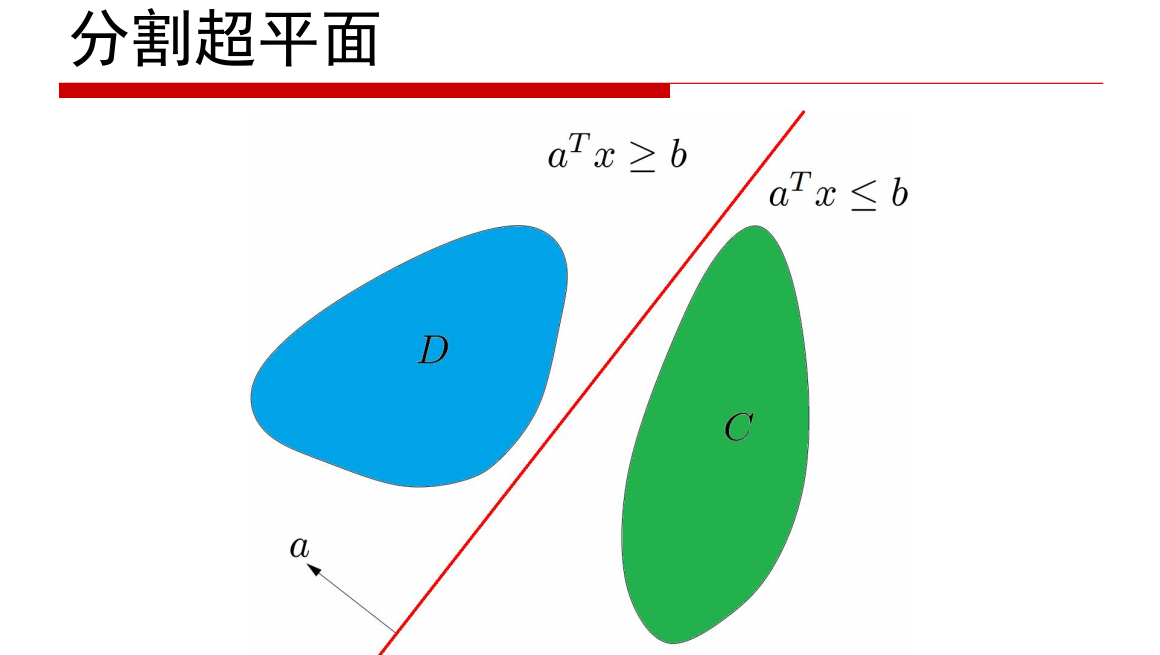
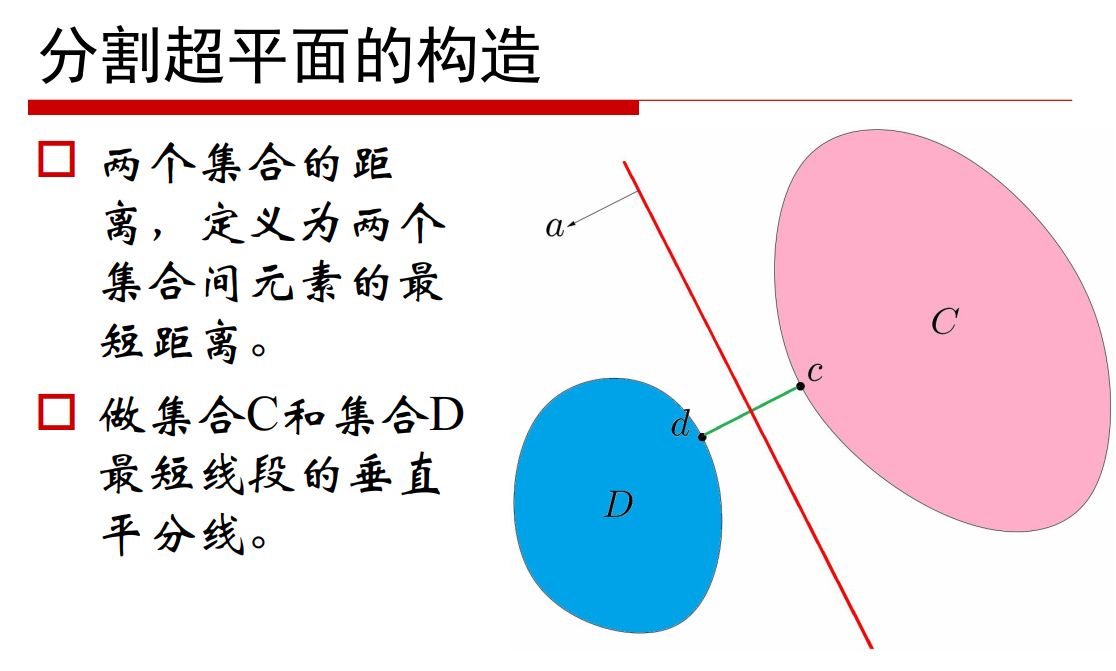
第一个是凸集,后两个不是




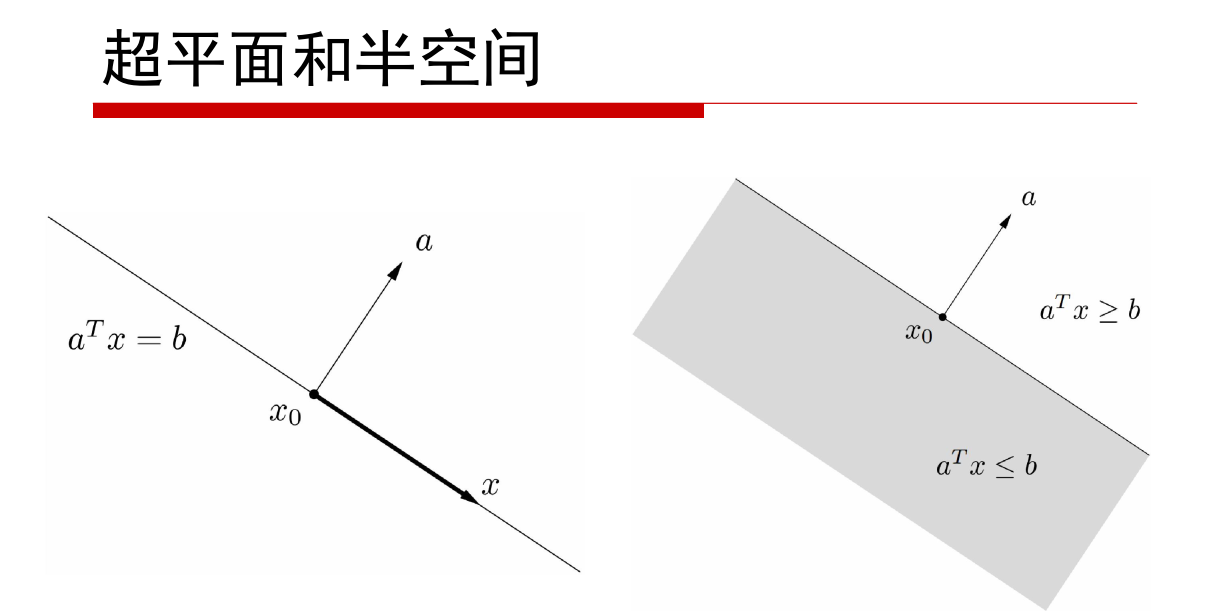
n维空间的超平面就是n-1维,类比于三维空间中的二维平面










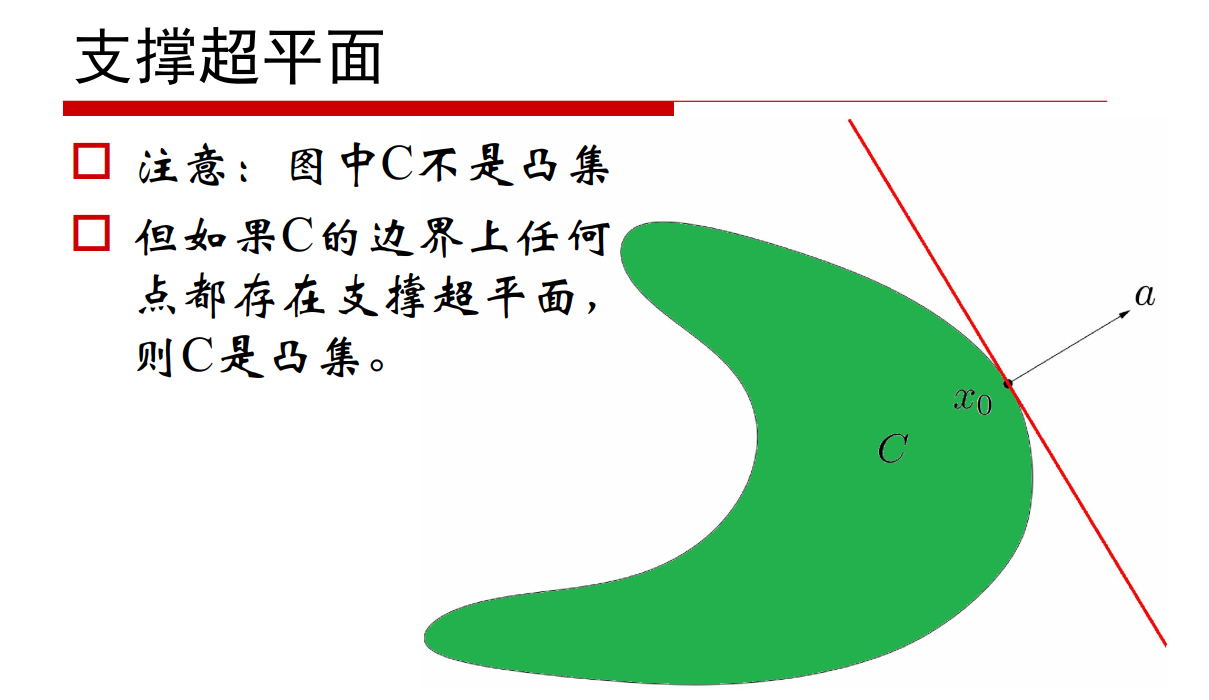
类似于切面,但不是,一个点可以有多个支撑超平面(过集合上这个点,不与集合上任意其他点相交)



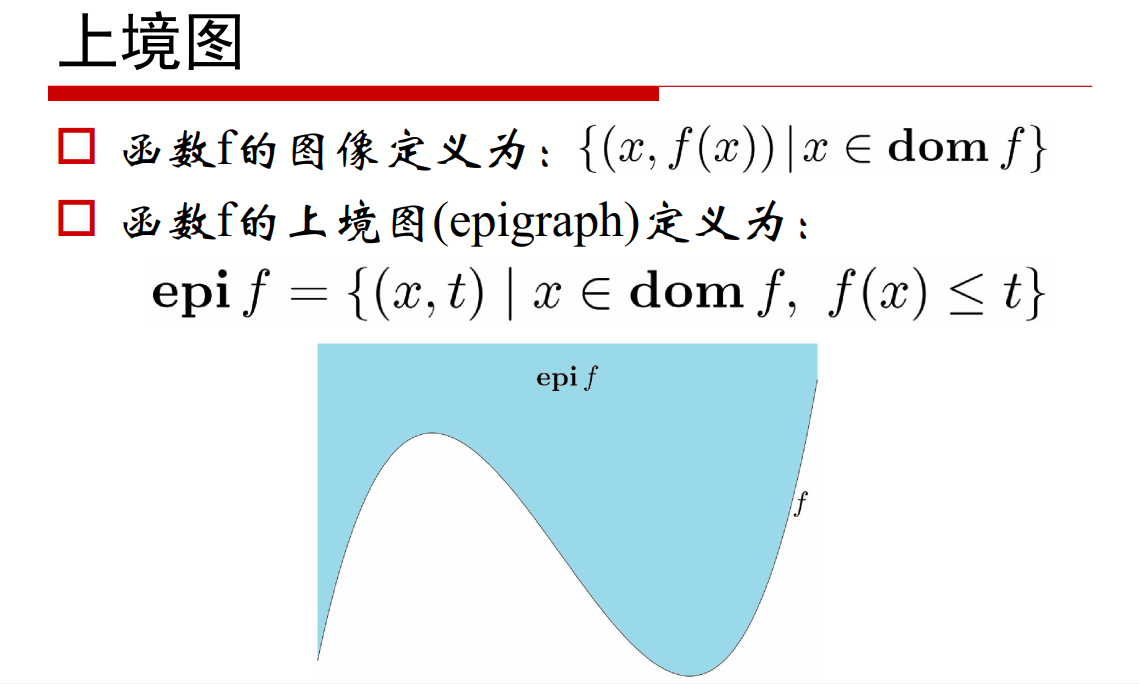





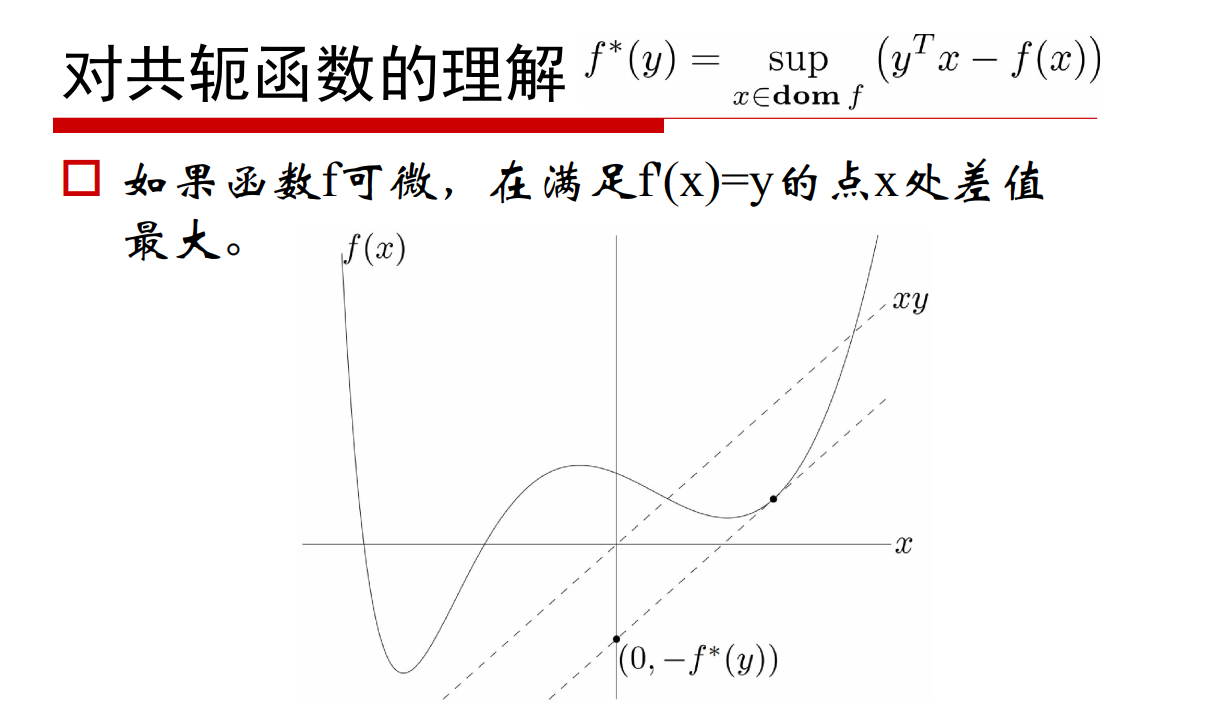






 本文解析了仿射包中的C1与仿射集中的C2的区别,并介绍了内点和相对内点的概念。通过实例解释了x=Θx1+(1-Θ)x2表达式的含义,区分了凸集与非凸集。此外还阐述了n维空间中超平面的概念以及支撑超平面的作用。
本文解析了仿射包中的C1与仿射集中的C2的区别,并介绍了内点和相对内点的概念。通过实例解释了x=Θx1+(1-Θ)x2表达式的含义,区分了凸集与非凸集。此外还阐述了n维空间中超平面的概念以及支撑超平面的作用。




注意仿射包中的集合C1与放松集中的C2不是指同一个,仿射包中的C1指的是线段、三角形、球体
仿射集中的C2值直线、平面、超平面。C1的仿射包就是仿射集C2


内点就是集合内一开始就存在于边界内部的点,相对内点是后来拿出来一个点,判断出它在集合内的点
x=Θx1+(1-Θ)x2表示x1到x2之间的点


第一个是凸集,后两个不是







n维空间的超平面就是n-1维,类比于三维空间中的二维平面














类似于切面,但不是,一个点可以有多个支撑超平面(过集合上这个点,不与集合上任意其他点相交)
















转载于:https://www.cnblogs.com/long5683/p/9404164.html
 1148
1148

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


