两个三维向量相乘公式_曲率半径参数公式新解

在二维的图像中，很多曲线难以直接地表示为y=y(x)的形式(如旋轮线)，此时我们往往采取用参数表示的方法去描述曲线，而用参数方程去描述曲率半径的公式较为复杂，且难以记忆。本文将采用物理的理解方法，并利用部分线性代数知识来理解并巧记曲率半径的参数表示公式。

曲率半径的参数表示

1

线性代数与矢量运算的相关知识回顾：

1、叉乘：两矢量叉乘得到一个新的矢量，其方向由右手螺旋法则来确定，其大小为两个矢量模长相乘并乘以两矢量的夹角正弦值，也可理解为：以这两个矢量为临边所形成的的平行四边形面积

例如上图中，平面内两个向量a×b所得向量大小即为absinθ，也可理解为平行四边形面积，方向垂直纸面向外

2、二阶行列式：二阶行列式的几何意义是两个矢量作为临边所形成的的平行四边形面积

将上图的两向量写为列向量的形式：

列出行列式(并取绝对值)：

此即该平行四边形的面积

3、结论：综合前两条可知，两个向量叉乘的模长与此二向量组成的行列式的绝对值相同。因此，在给定的平面内，两矢量叉乘所得矢量的模长可表示为行列式的形式，以上图为例，即：

2

为了与物理直观建立联系，我们将刻画曲线的参数取为时间t，利用物理中的运动学关系：

向心加速度=速度平方除以曲率半径

移项可得：

3

考虑任意一个运动过程：a为加速度，v为速度

记速度方向(即切向)的单位向量为τ(方向沿速度方向，大小为1)

有如下几何关系

考虑到第一部分所述的叉乘与正弦之间的关系，可以进一步改写为：

带入第二部分我们已经得到的公式：

最终得到：

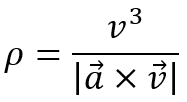
4

以时间t为参数，v与a作为向量可以被写为(按列向量处理)：

回顾第一部分我们得到的结论，此二向量叉乘的结果可表示为：

带入曲率半径表达式，得到最终结果：

虽然我们选取的参数是具有物理意义的时间t，但在数学上无论用什么参数去刻画，本质上是等价的，因此最后得到的结论是具有普适性的

笔者认为，此方法通过结合物理意义，不仅给出了一种快速推导曲率半径参数公式的方法，更重要的是若将二维曲线改为三维曲线，此时只能用参数去刻画空间曲线，而此公式的前半部分推导结果依然成立，具有更强的普适性

奇技淫巧学术驿站

生活不可万事都硬刚，学术也一样~

微信号 : qjyqxsyz

● 扫码关注我们