均值极差图控制上下限_年度质量回顾-单值移动极差

基于前文的讨论，总体均值和标准差未知，数据分布未知时，用

估计

做为控制限进行统计分析是不够准确精密的。连续型变量常用的控制图有单值-移动极差图、均值-极差图、均值-标准差图。单值-移动极差图用于不属于子组的单个观测值的监视，对于原料药的年度质量回顾是个不错的选择。

1. 极差R与平均移动极差^[1]

极差

平均移动极差

2. 单值控制图

中心线：

控制限：

正态分布下，

为

的无偏估计。

为标准正态总体分布下样本极差期望值1.128。

3. 极差控制图

中心线：

控制上限：

控制下限：0

为标准正态总体下样本极差分布的标准差值0.853。

4. 案例呈现 ^[2]

质量属性QA的批数据

• 正态性检验

QA数据正态检验图

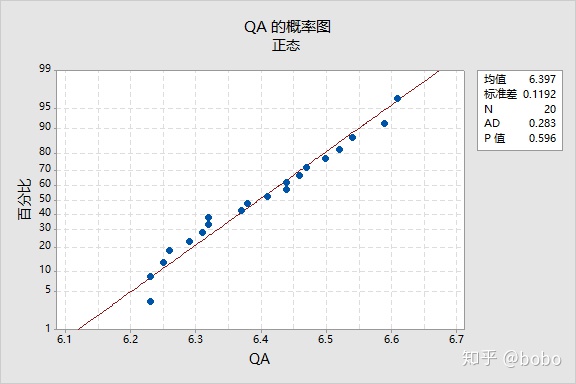
• 计算均值与平均移动极差

QA数据移动极差计算表

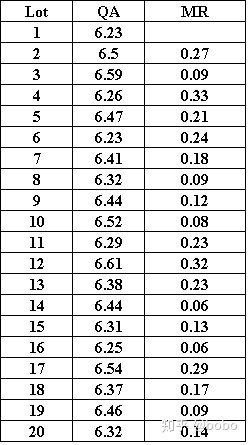
• 计算单值与极差控制图的控制限度

单值控制上限：

单值控制下限：

极差控制上限：

极差控制下限：0

• 判异

所有数据点均在控制限内，过程处于控制状态。

5. Note

• 正态分布

单值控制限计算式中，

为标准正态分布下样本极差期望值推演至一般正态分布得到的总体标准差

的无偏估计。故应首先进行正态性检验，如果数据大幅度偏斜，则可以尝试执行非正态变换以查看这能否更正非正态情况。如果过程自然产生非正态数据并且变换有效，则可使用变换后的数据的控制图来评估过程的稳定性。

• 样本量

推荐的样本量为100，样本量为100时，平均移动极差的相对标准差为0.076，已经足够小。

如果标准差非常大，应根据实际考虑推荐样本量是否可行。

对于“老产品”，直接用历史批次的均值和标准差，进行

分析即可。

对于“新”产品，如果具有的观测值数少于推荐的观测值数，则仍然可以使用控制图，但获得的是初步结果，因为控制限可能不精确（如上述20个样本的案例）。随着时间的推移 ，可在收集至所推荐数量的观测值之后重新评估标准差和控制限。

• 极差分布

极差控制图覆盖了三个标准差，是把样本极差分布近似看做正态分布，两者控制区间的长度基本相等。当子样极差观察值接近控制限端点时，往往可能做出错误的判断。

6. 从统计角度看持续工艺确认的必要性

统计值推荐样本值后，各种控制限估计已经足够精密，对总体的估计已经足够准确。

一般来说，数据统计至推荐样本值并不需要一年的时间，如果增加取样频次，甚至一个月内即可完成。

尤其对于“普通原因”引起的异常，发现越晚，中毒越深，代价越大。相比年度质量回顾，持续工艺确认能更早的发现不可预期的事件或趋势及可能的工艺控制问题和/或工艺改进的机会。

与其拉长战线，不如增加炮火，持续工艺确认很有必要！！！

参考

1. ^本文讨论移动步长为2的情形
2. ^暂用小样本呈现打开方式，年度批次数远大于20