惯性积计算实例_材料力学中关于截面形状的基本概念: 静矩，惯性矩，截面模量...

材料力学主要研究的对象是杆件和梁，那么这些结构的截面形状是如何影响结构的计算的，体现在哪些参数上。下面主要介绍下。

静矩: 静矩(面积乘以面内轴一次)把微元面积与各微元至截面上指定轴线距离乘积的积分称为截面的对指定轴的静矩:

静矩是截面形状参数，是构件的一个重要的截面特性。平面图形的面积A与其形心到某一坐标轴的距离的乘积称为平面图形对该轴的静矩。一般用S来表示。静距的数值可能为正也可能为负,也可能为0，静矩的量纲为长度的3次方，也就是L^3(mm^3或m^3)。有时候又称为截面面积矩。

注意：

惯性矩是乘以距离的二次方,静矩是乘以距离的一次方，惯性矩和面积矩(静矩)是有区别的。

惯性矩：(moment of inertia of an area)是一个几何量，通常被用作描述截面抵抗弯曲的性质。惯性矩的国际单位为(m^4)，恒为正值，其量纲是长度的四次方。即面积二次矩，也称面积惯性矩，而这个概念与质量惯性矩(即转动惯量)是不同概念。

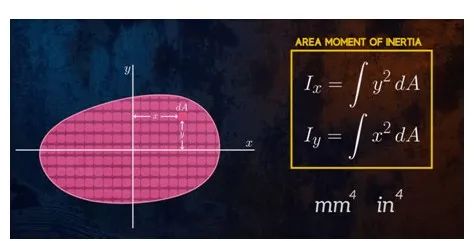
如下图所示，在任意平面内，将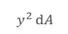、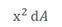分别称为微面积对x、y轴的惯性矩，它们在整个图形范围内的积分，分别定义为此平面图形对于x、y轴的惯性矩，简称惯性矩。

惯性半径：

在工程计算中，把惯性矩写成：

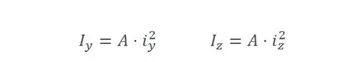
       或表示为

 

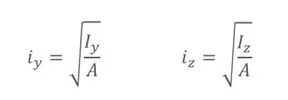
      式中，A为平面图形的面积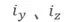，分别称为平面图形对y、z轴的惯性半径，其量纲是长度的一次方，常用单位是mm。

平行移轴定理：平面图形对任一对正交坐标的惯性积，等于图形对于与该轴平行的形心轴的惯性矩加上图形面积与二轴(形心轴与坐标轴)间距离平方的乘积。

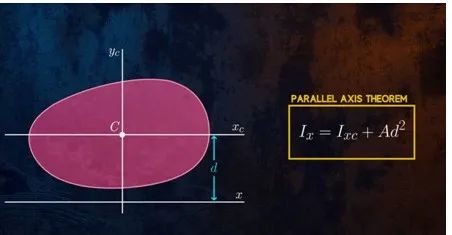
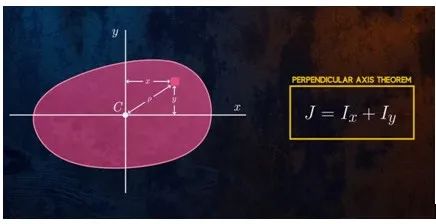
极惯性矩：截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩。

转轴公式：

对于形状复杂或没有对称轴的图形，即使形心位置确定了，也很难用直观的方法判定形心主惯性轴的位置。

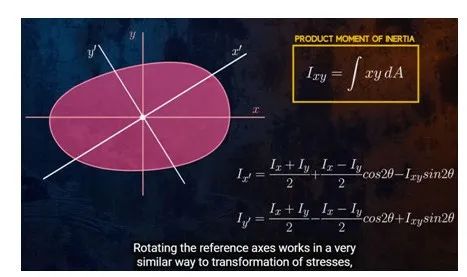
主惯性矩： 惯性积(I_xy,I_yz,I_zx)等于零的一对正交坐标轴称为主惯性轴。图形对于主惯性轴的惯性矩为主惯性矩。当一对主惯性轴的交点和截面的形心重合时，则这对轴为形心主惯性轴。图形对于形心主惯性轴的惯性矩为形心主惯性矩。

对于组合图形，惯性矩可以通过叠加计算：

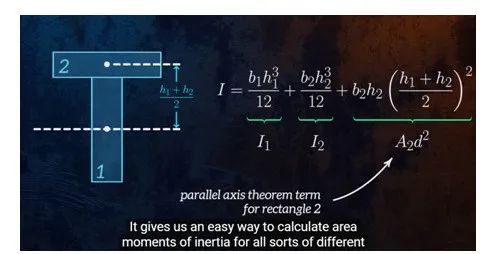
具体的应用：

1. 梁在纯弯曲的状态下，挠度为：

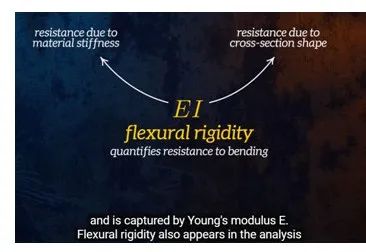
一定的弯矩下，抗弯刚度(杨氏模量×惯性矩)越大，挠度变化越小。

2. 对于杆的屈曲：可以通过抗弯刚度计算临界屈曲的应力。

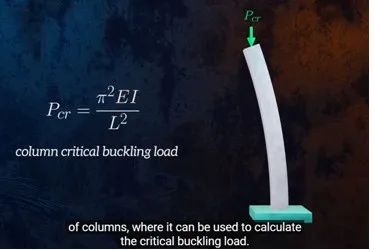
3. 在模态计算时，针对弯曲的振型(一般基频为结构的弯曲)，在不改变结构约束的情况下，最快捷提高固有频率的方式，就是增加(振幅比较大)根部截面的面积，也就是所谓的加筋，增加抗弯刚度可以提升固有频率。

截面模量(section modulus)：模量又叫截面抵抗矩也叫抗弯截面系数，是构件的一个重要的截面特性。被弯曲构件的横截面绕其中性轴的惯性矩除以由中性轴到截面最外边缘的距离。截面抵抗矩(W)就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值，即W=I/y，它用以计算零件、构件的抗弯强度和抗扭强度，或者用以计算在给定的弯矩或扭矩条件下截面上的最大应力，在力学计算中有着很大的作用。单位为毫米的三次方，截面的抗弯和抗扭强度与相应的截面系数成正比。

一些常见的图形的惯性矩及截面模量公式：

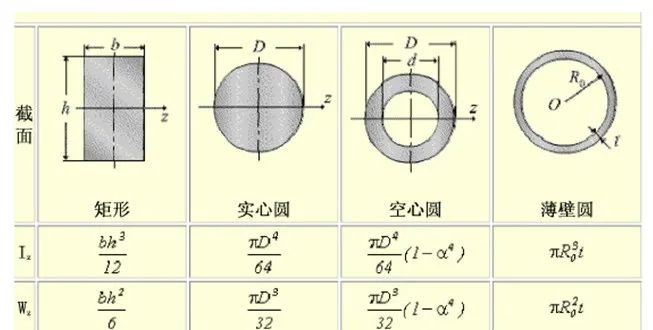
可以通过查机械手册，查出相应的型钢对应的截面模量和惯性矩，从而选择更优的抵抗弯曲或扭转的截面设计(比如工字钢)。